핵심은 5-6-10 시그마가 없다는 것입니다. 예, 하지만 테스트가 필요합니다. 그러나 그것은 정상일 수 있습니다.
가능성이 거의 없습니다. 일반적으로 정규 분포는 "큰" 확률 변수가 어떤 방식으로(그러나 동일하게) 분포된 많은 수의 "작은" 확률 변수의 합인 자연에서 발생합니다. 생생한 예가 브라운 운동인데, 이미 다음 지부에서 너무 많은 페이지를 할애했습니다. 시장의 경우 가격 형성의 법칙은 이와는 거리가 있습니다. 정상적인 것을 얻으려면 매우 많은 양의 외부 "소음"이 필요하기 때문입니다. 이는 유통 형성의 주요 요소여야 합니다. 그러나 우리는 시장 가격이 소음이라고 생각하지 않습니다. 그렇지 않습니까?
어딘가에 나는 심지어 차이점을 보여주는 표지판을 가지고있었습니다. 분포의 처음 두 모멘트를 취하여 근사법칙의 모멘트로 간주하면 빈도의 차이는 3, 4, 5 등입니다. 시그마는 계산하기 쉽습니다.
정확한 수치는 기억나지 않지만 실제 편차 빈도는 3시그마 곱하기 3-4배 더 많은 가우스입니다(가우스에 따르면 - 0.3%, 실제로 - 1% 이상). 실생활에서 4시그마의 편차는 이미 가우시안보다 15배 정도 더 많이 발생하는데, 5시그마의 경우 그 차이는 수백배는 아니더라도 수십배입니다. 등.
위험을 평가하지 않는 한 가우스인지 아닌지는 상관하지 않습니다.
PS 그건 그렇고, Taleb에 따르면 LTCM은 위험을 과소 평가했기 때문에 정확히 무너졌습니다. 10시그마 편차는 무시할 수 있는 이벤트로 간주되었습니다. 그리고 그것은 방금 일어났습니다.
정확한 수치는 기억나지 않지만 실제 편차 빈도는 3시그마 곱하기 3-4배 더 많은 가우스입니다(가우스에 따르면 - 0.3%, 실제로 - 1% 이상). 4시그마의 편차는 이미 15배 정도 가우시안보다 실생활에서 더 많이 발생하며, 5시그마의 경우 그 차이는 수십 배입니다. 등.
확인. 여기 데이터가 있습니다.우리는 서로를 오해하고 있는 것 같습니다. 이상에 대한 나의 격언은 발전기가 아니라 시장에 관한 것입니다. 첫 번째 증분의 분포를 만들고 확인합니다.
음, 진공 상태의 구형 말의 경우, 즉 보장된 정규 분포의 경우 그렇습니다. 그래서 실제 수익은 진공 상태의 말이 아닙니다. 커먼과 5, 6 s.k.o.가 있으며 10도 있습니다.
삼촌, 글쎄요, 여기 1971년부터 일광 절약 시간제에 대한 또 다른 사진이 있습니다. 단일 런지가 될 수 있습니다(그런데 아무 것도 없습니다 :), 가장 중요한 것은 이것이 패턴이 되지 않는다는 것입니다. 그래서?
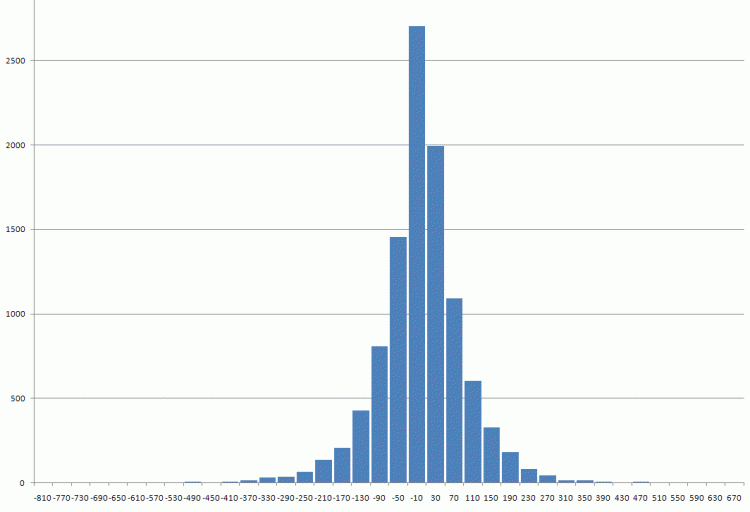
검증 데이터를 첨부합니다.1971년 이후 첫 파운드 차이
추신. 정지 상태를 확인해보세요 :)
삼촌, 글쎄요, 여기 1971년부터 일광 절약 시간제에 대한 또 다른 사진이 있습니다. 단일 런지가 될 수 있습니다(그런데 아무 것도 없습니다 :), 가장 중요한 것은 이것이 패턴이 되지 않는다는 것입니다. 그래서?
검증 데이터를 첨부합니다.1971년 이후 첫 파운드 차이
나는 그것을 눈으로 라플라스 분포라고 부르겠습니다.
나는 그것을 눈으로 라플라스 분포라고 부르겠습니다.
핵심은 5-6-10 시그마가 없다는 것입니다. 예, 하지만 테스트가 필요합니다. 그러나 그것은 정상일 수 있습니다.Ilya , 한 가지 제안이 있습니다. 이 분포를 정규 분포로 근사화하십시오. 그런 다음 실제 히스토그램과 가우스 곡선의 근사치가 서로 얼마나 다른지 살펴보십시오. 자신을 세 개의 시그마로 제한하지 말고 적어도 열 개의 시그마를 보십시오.
또 다른 간단한 테스트: 이 분포의 첫 번째 모멘트를 계산하고 정규 분포의 모멘트와 비교합니다.
금융 시리즈에서 뚱뚱한 꼬리 현상은 오랫동안 알려져 왔습니다. 나에게 무엇을 증명하고 싶습니까?
Ilya, 한 가지 제안이 있습니다. 이 분포를 가져와 정규 분포로 근사합니다. 그런 다음 실제 히스토그램과 가우스 곡선의 근사치가 서로 얼마나 다른지 살펴보십시오. 자신을 세 개의 시그마로 제한하지 말고 적어도 열 개의 시그마를 보십시오.
또 다른 간단한 테스트: 이 분포의 첫 번째 모멘트를 계산하고 정규 분포의 모멘트와 비교합니다.
금융 시리즈에서 뚱뚱한 꼬리 현상은 오랫동안 알려져 왔습니다. 나에게 무엇을 증명하고 싶습니까?
대화는 약 5-6-10 RMS였습니다. 나는 그들의 모습에서 어떤 규칙성을 보지 못한다.
핵심은 5-6-10 시그마가 없다는 것입니다. 예, 하지만 테스트가 필요합니다. 그러나 그것은 정상일 수 있습니다.가능성이 거의 없습니다. 일반적으로 정규 분포는 "큰" 확률 변수가 어떤 방식으로(그러나 동일하게) 분포된 많은 수의 "작은" 확률 변수의 합인 자연에서 발생합니다. 생생한 예가 브라운 운동인데, 이미 다음 지부에서 너무 많은 페이지를 할애했습니다. 시장의 경우 가격 형성의 법칙은 이와는 거리가 있습니다. 정상적인 것을 얻으려면 매우 많은 양의 외부 "소음"이 필요하기 때문입니다. 이는 유통 형성의 주요 요소여야 합니다. 그러나 우리는 시장 가격이 소음이라고 생각하지 않습니다. 그렇지 않습니까?
차트에서는 순전히 시각적으로 이러한 5-6-10을 볼 수 없습니다.
어딘가에 나는 심지어 차이점을 보여주는 표지판을 가지고있었습니다. 분포의 처음 두 모멘트를 취하여 근사법칙의 모멘트로 간주하면 빈도의 차이는 3, 4, 5 등입니다. 시그마는 계산하기 쉽습니다.
정확한 수치는 기억나지 않지만 실제 편차 빈도는 3시그마 곱하기 3-4배 더 많은 가우스입니다(가우스에 따르면 - 0.3%, 실제로 - 1% 이상). 실생활에서 4시그마의 편차는 이미 가우시안보다 15배 정도 더 많이 발생하는데, 5시그마의 경우 그 차이는 수백배는 아니더라도 수십배입니다. 등.
위험을 평가하지 않는 한 가우스인지 아닌지는 상관하지 않습니다.
PS 그건 그렇고, Taleb에 따르면 LTCM은 위험을 과소 평가했기 때문에 정확히 무너졌습니다. 10시그마 편차는 무시할 수 있는 이벤트로 간주되었습니다. 그리고 그것은 방금 일어났습니다.
정확한 수치는 기억나지 않지만 실제 편차 빈도는 3시그마 곱하기 3-4배 더 많은 가우스입니다(가우스에 따르면 - 0.3%, 실제로 - 1% 이상). 4시그마의 편차는 이미 15배 정도 가우시안보다 실생활에서 더 많이 발생하며, 5시그마의 경우 그 차이는 수십 배입니다. 등.
... 다시 한 번 라플라스를 옹호하는 증언
위험을 평가하지 않는 한 가우스인지 아닌지는 상관하지 않습니다.
위험 평가에 접근하는 방법을 알려주시겠습니까?