ライブラリ: 統計関数

新しいコメント
 

統計関数:

時系列を記述する値の計算を可能にする統計関数のセット

作者: Haruna Nakamura

 
どのように実行しますか？
 
ziad8978:
どのように実装するのですか？

私のライブラリに興味を持っていただきありがとうございます。使い方はとても簡単で、主に1次元の配列を操作します。

例えば、
detrend(timeSerie, detrendResultArray)を 使えば、時系列から線形トレンドを簡単に取り除くことができます；

timeSerieは価格で埋め尽くされた配列で、detrendResultArrayは結果が格納される空の配列でなければなりません。
したがって、関数を呼び出した後には、デトレンドされた時系列を持つ配列ができ、それに対してさらなる分析（例えば、時系列が静止しているかどうかのチェック）を行うことができます。

例えば、Currency1(場合によっては逆行)の配列があると仮定して、その次の値を予測することができます：

double detrendedSerie[];
double forecastedValue;

//(配列の最後の値が最新の価格となる)
detrend(Currency1, detrendedSerie);

if(dickeyFuller(detrendedSerie)){
  forecastedValue = AR1(detrendedSerie); 
}

if(forecastedValue > detrendedSerie[ArraySize(detrendedSerie)-1]){
  //購入
}else{
  //販売
}

もう1つの興味深い関数は符号付き積分です。現在の形でこれを使うのは非常に簡単です。関数を呼び出して、限界と多項式次数（これは小さくてもかまいません）を定義し、
、与えられた積分の良い近似を得るだけです。foo "関数を編集して、f(x) = x以外の関数を積分することもできます。

 
ziad8978:
どのように実行しますか？
 
ziad8978:
どのように実行しますか？
 
tinakorn kunchai:
ファイル:
WP_20150602_17_33_10_Selfie.jpg  1287 kb
 
Herajika、このコードを教えてくれて本当にありがとう！
 
Rodrigo Malacarne:
Herajika、このコードをシェアしてくれて本当にありがとう！
気に入っていただけて嬉しいです！このライブラリを使ってEA/Indicatorを作ったら、ここにリンクを貼ってください。
 
Haruna Nakamura:
気に入っていただけてうれしいです！このライブラリを使って何かEA/Indicatorを作成したら、ここにリンクを貼り付けてください。

Herajikaさん、こんにちは、

HerajikaさんのコードにあるDickey-Fuller検定統計量を他の統計/数学ソフトウェアで再現しようとしています。特にWolfram Mathematicaを使っています。

元記事（Scribdより）のデータを考えてみてください：

double data[] = {6109.58, 6157.84, 5850.22, 5976.63, 6382.12, 6437.74, 6877.68, 6611.79, 7040.23, 6842.36, 6512.78, 6699.44, 
                 6700.20, 7092.49, 7558.50, 7664.99, 7589.78, 7366.89, 6931.43, 5530.71, 5611.90, 6208.28, 6343.87, 6485.84};

あなたのコードを使って検定統計量を得るために、以下のコードで見られるように、Print関数の前のコメントを削除しました：

bool dickeyFuller(double &arr[])
  {
// n=25 50 100 250 500 >500
// {-2.62, -2.60, -2.58, -2.57, -2.57, -2.57};
   double cVal;
   bool result;
   int n=ArraySize(arr);
   double tValue;
   double corrCoeff;
   double copyArr[];
   double difference[];
   ArrayResize(difference,n-1);
//---
   for(int i=0; i<n-1; i++)
     {
      difference[i]=arr[i+1]-arr[i];
     }
//---
   ArrayCopy(copyArr,arr,0,0,n-1);
   corrCoeff=correlation(copyArr,difference);
   tValue=corrCoeff*MathSqrt((n-2)/1-MathPow(corrCoeff,2));
//---
   if(n<25)
     {
      cVal=-2.62;
        }else{
      if(n>=25 && n<50)
        {
         cVal=-2.60;
           }else{
         if(n>=50 && n<100)
           {
            cVal=-2.58;
              }else{
            cVal=-2.57;
           }
        }
     }
   Print(tValue); //--- テスト統計？
   result=tValue>cVal;
   return(result);
  }

前述の通り、私はテストの結論ではなく、テストの統計量自体に興味があります。この意味で、教えていただいたコードを使用すると、次のようになります：

void OnStart()
  {
//--- 出典：http://pt.scribd.com/doc/80877200/How-to-do-a-Dickey-Fuller-Test-using-Excel#
   double data[] = {6109.58, 6157.84, 5850.22, 5976.63, 6382.12, 6437.74, 6877.68, 6611.79, 7040.23, 6842.36, 6512.78, 6699.44, 
                     6700.20, 7092.49, 7558.50, 7664.99, 7589.78, 7366.89, 6931.43, 5530.71, 5611.90, 6208.28, 6343.87, 6485.84};
//---
   dickeyFuller(data);
  }

検定統計の行を印刷すると、次のようになる：

-1.719791886975595

しかし、元の記事ではt統計量が1.8125であると書かれています。

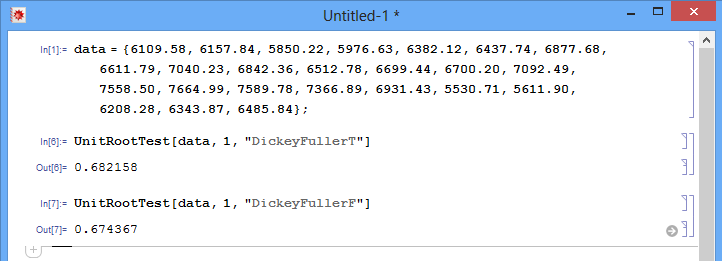
しかし，同じデータセットでWolfram Mathematica を使うと，次のようになります．


3つの検定で3つの異なる検定結果が出る原因について何かおわかりになりますか？


Malacarne

 

こんにちは！記事(http://pt.scribd.com/doc/80877200/How-to-do-a-Dickey-Fuller-Test-using-Excel#) の結果と私の実装の違いについてですが、
、言及されているサイトでは、符号(+, -)の表示に問題があることにご注意ください。従って，記事で提示されている結果は，実際には-1.8125です．

Wolfram Mathematicaとの違いについては、多分、異なる傾向の実装が異なる臨界値を使い、異なるtValueを計算しているのでしょう。Matlabで同じことをすると、
、また別の結果（0.6518）が出た。

しかし、エクセルで同じことを試すと、-1.8125に近いものが表示されるはずです。


ヘラジカ

 
Haruna Nakamura:

こんにちは！記事(http://pt.scribd.com/doc/80877200/How-to-do-a-Dickey-Fuller-Test-using-Excel#) の結果と私の実装の違いについてですが、
、言及されているサイトでは、符号(+, -)の表示に問題があることにご注意ください。従って，記事で提示されている結果は，実際には-1.8125です．

Wolfram Mathematicaとの違いについては、多分、異なる傾向の実装が異なる臨界値を使い、異なるtValueを計算しているのでしょう。Matlabで同じことをすると、
、また別の結果（0.6518）が出た。

しかし、エクセルで同じことを試すと、-1.8125に近いものが表示されるはずです。


Herajika

こんにちは、Herajika、

お返事ありがとうございます。では、この場合、どのような統計が正しいのでしょうか？

元記事では、検定統計の値が間違っているのでしょうか？


Malacarne

追伸：Mathematicaでは，"TestStatistic "をオプションとして使わなければ，MatLabと比較して同じような結果が得られます．

123
新しいコメント