こんにちは、Ndawana
まず最初に、記事とAI神話の単純化に感謝するよ。)この記事から生成されたシグナルを私のコードで使おうとしています。
あなたのコードで単純な配列の代わりにベクトルを使った理由を説明してもらえますか?
Anil Varma #:
こんにちは、ンダワナ
まず最初に、記事とAI神話の単純化に感謝するよ。)この記事から生成されたシグナルを私のコードで使おうとしています。
あなたのコードで単純な配列の代わりにベクトルを使った理由を説明してもらえますか?
私がベクターを好むのは、ベクターにしか使えない特別な関数があるからです。その特別な関数に加えて、ベクターはすべての要素に対して一度に計算を実行することもできます。
。
//+------------------------------------------------------------------+ //|アニルmq5||アニル //|ガムチライ・ゾロロ・ンダワナ|Gamuchirai Zororo Ndawana|ガムチライ・ゾロロ・ンダワナ //|https://www.mql5.com/ja/gamuchiraindawa||日本 //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| スクリプト・プログラム開始機能| //+------------------------------------------------------------------+ void OnStart() { //--- 配列に関する私の問題はこうだ。 double anil_array[3]; ArrayFill(anil_array,0,3,0); ArrayPrint(anil_array); //--- 計算を実行するために、すべての要素を反復処理しなければならない。 for(int i = 0; i < 3; i++) { anil_array[i] += 1; } ArrayPrint(anil_array); //--- ベクトルでも同じ操作を行う。 vector anil_vector = vector::Zeros(3); //ゼロでいっぱいの配列にシミラーする Print(anil_vector); //--- ベクトルによって、すべての要素に対して一度に計算を行うことができる。 anil_vector = anil_vector + 1; Print(anil_vector); } //+------------------------------------------------------------------+
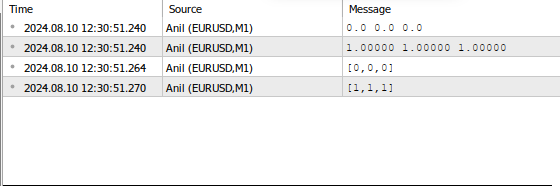 .
.
もし将来、役に立つような計算を思いついたとしたら、ベクターを使っているので、コードベースの修正がとても簡単になると想像してください。
取引の機会を逃しています。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事「古典的な戦略をPythonで再構築する(第2回):ボリンジャーバンドのブレイクアウト」はパブリッシュされました:
本稿では、線形判別分析(LDA: Linear Discriminant Analysis)とボリンジャーバンドを統合し、戦略的市場参入シグナルの生成を目的としたカテゴリ別ゾーン予測を活用する取引戦略を考察します。
人工知能(AI: Artificial Intelligence)という言葉は、歴史上、最も誤解を招きやすい命名のひとつであることは間違いありません。この記事を読んでいただければ、AIという名前が適切でないと感じるかもしれません。私が問題視しているのは、「知能」という言葉です。AIモデルは、人間の意味での知能を持つわけではなく、実際には最適化アルゴリズムを知的に応用したものにすぎません。
AIモデルは、主にシステム内のエラーを最小化したり、報酬を最大化することを目指します。しかし、モデルが導き出す解決策は、常に現実的とは限りません。たとえば、取引口座の損失を最小限に抑えることを目標にしたAIシステムは、「取引を行わない」という結論に達する可能性があります。この解決策は数学的には問題を満たしていますが、実際の取引では現実的ではありません。
私たち、いわゆる知的AIの実践者は、慎重に計画された制約を通してモデルを導く必要があります。この記事では、ボリンジャーバンドを活用してAIモデルに指示を与えます。ボリンジャーバンドを基に、価格がどの瞬間にも存在し得る4つのゾーンを特定します。価格は常にこの4つのゾーンのいずれかに位置します。
価格がこれら4つのゾーン間をどのように移動するかを理解するためにモデルを訓練し、次に価格が移動するゾーンを予測します。取引シグナルは、価格があるゾーンから別のゾーンに移動するたびに生成されます。たとえば、モデルがゾーン2からゾーン1に価格が移動すると予測した場合、これを上昇のサインと捉え、買い注文を発行します。このモデルとエキスパートアドバイザー(EA)は、完全にMQL5でネイティブに実装されています。
ボリンジャーバンドは、トレンドフォロー戦略や転換点の特定など、さまざまな取引戦略に利用されます。この指標は、厳密には指数移動平均(EMA)を基に構成され、通常は証券の終値を平滑化します。EMAは2本のバンドに挟まれており、1本はEMAの上、もう1本はEMAの下に配置され、これらのバンドは通常2標準偏差に設定されています。
作者: Gamuchirai Zororo Ndawana