Если оба процесса независимые, то оба они просто шум. Если ты складываешь или вычитаешь два шума, то получаешь просто третий шум. Т.е. результирующий процесс будет
y(i) = y(i-1) + e(i), где e(i) = b(i)+s(i) или e(i) = b(i)-s(i); + или - это не имеет значения.
Случайное блуждание чистой воды. Мелкие модификации, типа типа обрезания паникёров, серьёзно ничего не изменят. Только если твои процессы будут не независимые, то могут начаться чудеса.
Не очень понял. Типа y(i) = y(i-1) + e(i) * i, где e(i) = b(i)+s(i)? Не удваивается, но возрастает. Удваивание слишком быстро вырастет. Даже простое умножение на i даёт вот такой рост приращений
Однако, результирующий процесс y(i) остаётся нормальным, чего мы и ожидаем от случайного блуждания.
Хотя оно так может и не кажется на первый взгляд, но это только из-за изменения масштаба
avatara>>: На форуме часто в пылу дискуссии утверждается, что блуждание цены абсолютно случайно. Пускай не всегда. Но случайность и не... сложно якобы отличить. Теоремы арксинуса и двойного логарифма периодически обсуждаются или цитируются напрямую, либо только выводы. Мутно как то... У меня вопрос к теоретикам и практикам. Изучал ли кто "блуждание после соударения"? Постановка задачи следующая - есть два условных героя "БАЙ" и "СЕЛ". Пускай генерится некое приращение для каждого из них. В зависимости от героя назовём их "наступательным приращением" и "оборонительной силой". ...
avatara>>: супер! О удваивании следующее "прак...ое" наблюдение. Если на предыдущем шаге герой получил желаемое приращение (т.е |y(i)-y(i-1)|>= сила героя на i-том шаге, то его сгенерированную силу ( в том числе с минусом - сомнения) на i+1 шаге следует удвоить.
речь о моделировании случайных блужданий, что делается как правило стационарными распределниями - нормальным или дискретным. Можно наверное изголиться и смоделировать нестационарным. Сумма или разность нестационарных распределений будет так же нестационарна как правило, хотя есть исключения, которые лежат в основе коинтеграциии например
Если параметры распределений Б и С различны, то формулы для вычисления МО и дисперсии будут сложнее, но все равно будет такое же распредление
これは、CとBが安定した分布をしている場合です。その場合、そうですね、安定分布の和が安定分布に等しくなりますね。そうでなければ、いや、分布の異なるCとBの和や差は、とんでもない分布になる。
Если оба процесса независимые, то оба они просто шум. Если ты складываешь или вычитаешь два шума, то получаешь просто третий шум. Т.е. результирующий процесс будет
y(i) = y(i-1) + e(i), где e(i) = b(i)+s(i) или e(i) = b(i)-s(i); + или - это не имеет значения.
Случайное блуждание чистой воды. Мелкие модификации, типа типа обрезания паникёров, серьёзно ничего не изменят. Только если твои процессы будут не независимые, то могут начаться чудеса.
ご返信ありがとうございました。
もうひとつ、アルゴリズムに修正を加えてもいいですか?
主人公が「増量」した場合、その力と疑問は2倍になる。
では、このランダムなプラクティショナルのプロセスはどのように見えるのでしょうか。
同様にモデリングしたものを知っている - ベル/パイプを見ることができますか?これは、CとBが安定した分布をしている場合です。その場合、そうですね、安定分布の和が安定分布に等しくなりますね。そうでなければ、いや、分布の異なるCとBの和や差は、とんでもない分布になる。
ランダムウォークのモデル化については、通常、定常分布(正規分布または離散分布)を使って行われます。おそらく、それを回避して非定常としてモデル化することができるのでしょう。非定常分布の和や差も原則として非定常となるが、コインテグレーションの根底にある例外がある。
Спасибо за ответ.
можно ввести еще одну поправку к алгоритму?
Если герой получил свое "приращение" - его силы и сомнения удваиваются.
Как тогда этот случайно праксиологический процесс будет смотреться?
Зная, что вы похожее моделировали - можно колокол/трубу глянуть?よくわからないんですけどね。y(i) = y(i-1) + e(i) * i で、e(i) = b(i)+s(i) という感じでしょうか?
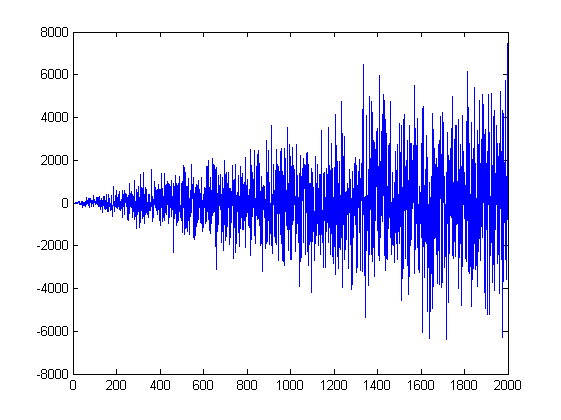
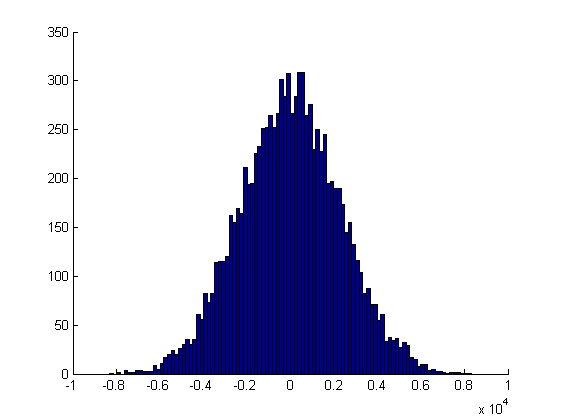
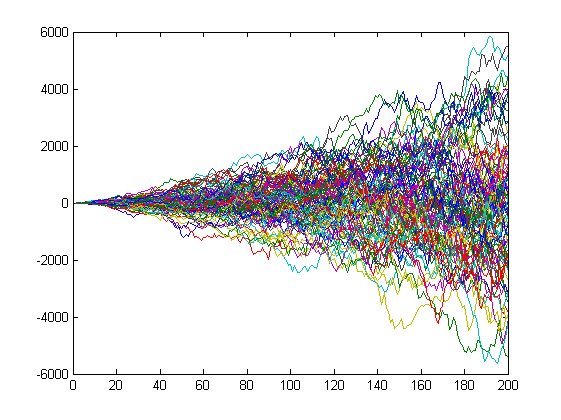
倍増ではなく、増加です。倍率が高くなりすぎてしまう。単純なiの掛け算でも、このように増分が増えていきます。
しかし、結果として得られる過程y(i)は正規分布のままであり、これはランダムウォークから期待されるものである。
一見するとそうでもないように見えますが、これはスケールが変わったからに他なりません
Не очень понял. Типа y(i) = y(i-1) + e(i) * i, где e(i) = b(i)+s(i)?
Не удваивается, но возрастает. Удваивание слишком быстро вырастет. Даже простое умножение на i даёт вот такой рост приращений
Однако, результирующий процесс y(i) остаётся нормальным, чего мы и ожидаем от случайного блуждания.
Хотя оно так может и не кажется на первый взгляд, но это только из-за изменения масштаба
倍増については、次のような「実用的」な観測がなされている。
前のステップでヒーローが望ましい増分を得た場合(つまり|y(i)-y(i-1)|>=i番目のステップでのヒーローの強さ)、i+1ステップでの彼の生成強度は(マイナス-疑いを含む)2倍でなければならない。
ここでアークサインは増幅するはずだが、よくわからない。符号分散が邪魔をする;)
---
生意気なお願いですが、実装の長さを500に増やしてください。 ファイアー
На форуме часто в пылу дискуссии утверждается, что блуждание цены абсолютно случайно.
Пускай не всегда. Но случайность и не... сложно якобы отличить.
Теоремы арксинуса и двойного логарифма периодически обсуждаются или цитируются напрямую, либо только выводы.
Мутно как то...
У меня вопрос к теоретикам и практикам.
Изучал ли кто "блуждание после соударения"?
Постановка задачи следующая - есть два условных героя "БАЙ" и "СЕЛ".
Пускай генерится некое приращение для каждого из них.
В зависимости от героя назовём их "наступательным приращением" и "оборонительной силой".
...
もし、その増分が攻撃的なものであれば、慣習上、機動性において防御的な増分に優先されなければならない。
生成後のLFGに定数を追加するか、LFGの範囲をシフトして設定する必要があります。
そうすると、攻めと守りが1つずつになる。そうでないと、誰が守りに入っているのかがわからない。
倍増については、次のような「実用的」な観測がなされている。
前のステップでヒーローが望ましい増分を得た場合(つまり|y(i)-y(i-1)|>=ステップiにおけるヒーローの体力)、ステップi+1における彼の生成体力(マイナス-疑いを含む)は2倍になるはずである。
ここでアークサインは増幅するはずだが、よくわからない。符号分散が邪魔をする;)
そんなコーヒーリーフの当て字で市場流通を見極めたい(というか、合わせたい)のでしょうか?
супер!
О удваивании следующее "прак...ое" наблюдение.
Если на предыдущем шаге герой получил желаемое приращение (т.е |y(i)-y(i-1)|>= сила героя на i-том шаге, то его сгенерированную силу ( в том числе с минусом - сомнения) на i+1 шаге следует удвоить.
意味がないんです。このような操作により、増分の分布は変化し、BとCが正規分布であったとしても、大きな尾を引くことになりますが、結果のプロセスの性質は変わりません - ランダムウォークのまま、正規分布となるでしょう。ランダムウォークは、第3モーメントが0である限り、つまり対称である限り、増分の分布は気にしない。
речь о моделировании случайных блужданий, что делается как правило стационарными распределниями - нормальным или дискретным. Можно наверное изголиться и смоделировать нестационарным. Сумма или разность нестационарных распределений будет так же нестационарна как правило, хотя есть исключения, которые лежат в основе коинтеграциии например
暖かさと柔らかさ、つまり定常性と分布を混同しないようにしましょう。両者には何の関係もありません。ランダムウォークは正規分布を持ちますが、定常的ではありません。一様分布は 定常ですが、2つの一様分布の和は一様分布になりません。これは、安定分布だけの 性質(どんな線形操作でも分布の型・形状を保持する)である。
暖かさと柔らかさ、つまり定常性と分布を混同しないようにしましょう。両者には何の関係もありません。ランダムウォークは正規分布を持ちますが、定常的ではありません。一様分布は 定常ですが、2つの一様分布の和は一様分布になりません。これは、安定分布だけの 性質(どんな線形操作でも分布の型・形状を保持する)である。
関係ないわけがない。正規分布は静止しているし、NRで分布するSBの増分は 静止しているし、もともと増分の話なんです。
SBそのもの(インクリメントの累積和)については、前回の投稿にあったような「重い尾」を引くことはないでしょう。なぜなら、時刻tの SB自体も正規分布しているが、1増分(原点からの時刻t)よりもt倍大きな分散を持つからである。はい、SB分布の分散は時間が長くなるにつれて大きくなります。例えば3シグマ以上の重いテールですが、SBの場合、特定の時間における分散を計算すれば(解析的に計算できます)、正規の場合と同じになります。
SBプロセス自体は定常ではなく、単位根I(1)を持つ劣後プロセス、つまり最初の差分(増分)が定常分布であることは同意するhttps://www.mql5.com/go?link=http://window.edu.ru/catalog/pdf2txt/141/28141/11363?p_page=55 しかし、非定常分布は必ずしも重いテールを持つわけではなく、この場合はテールがないことになります。
HPは非定常だと思いますか?あるいは、すべての連続分布について、それが定常かどうかを言うことはできないのでしょうか?:)