直感的なテスト - ページ 13 1...678910111213141516171819 新しいコメント Alexey Subbotin 2009.11.28 20:12 #121 IlyaA >> : >> OKです。以下はそのデータです。 お互いに誤解しているようです。私の異常に対する感情は、発電機ではなく、市場に適用されるものです。最初の増分の分布を構築して、自分の目で確かめてください。 ilyaa 2009.11.28 20:26 #122 Mathemat >> : 真空中の球形の馬の場合、つまり正規分布が保証されている場合は、そうですね、ありえません。まあ、本物は真空中の馬ではありませんからね。5や6のS.C.E.もあれば、10のS.C.E.もあるんです。 おじさん、お願いします!今もう一枚、1971年のポンド、ダイアリーの写真です。ランジは1回かもしれませんが(ちなみに1回はないです : )、一番大事なのは、それがパターンにならないことです。そうだろ? 1971年以来のポンド差。 チェック用のデータを同封しています。 >>S. 定常性のチェックを受けるべきかもしれません :) ファイル: data_1.rar 127 kb Alexey Subbotin 2009.11.28 20:28 #123 IlyaA >> : おじさん、お願いします!今もう一枚、1971年のポンド、ダイアリーの写真です。ランジは1回かもしれませんが(ちなみに1回はないです : )、一番大事なのは、それがパターンにならないことです。そうだろ? 1971年以来のポンド差 チェック用のデータを添付します。 目測でラプラス分布と言うところでしょうか。 ilyaa 2009.11.28 20:31 #124 alsu >> : 目で見てラプラス分布と呼べるような 5-6-10のシグマがないのがポイントです。それ以外の場合は、そうですが、テストする必要があります。それでもいいのかもしれない。 Sceptic Philozoff 2009.11.28 20:39 #125 イリヤ ここで提案なんですが、この分布を正規分布で近似してみましょう。そして、実際のヒストグラムとガウス曲線の近似値がどれだけ違うかを確認します。3シグマにこだわらず、最低でも10シグマは調べましょう。 もう一つの簡単なチェックは、この分布の最初のモーメントを計算し、正規分布のモーメントと比較することです。 金融系列におけるファットテールという現象は古くから知られている。何を証明したいんだ? ilyaa 2009.11.28 20:45 #126 Mathemat >> : イリヤ ここで提案なんですが、この分布を正規分布で近似してみましょう。そして、実際のヒストグラムとガウス曲線の近似値がどれだけ違うかを確認します。3シグマにこだわらず、最低でも10シグマは調べましょう。 もう一つの簡単なチェックは、この分布の最初のモーメントを計算し、正規分布のモーメントと比較することです。 金融系列におけるファットテールという現象は古くから知られている。何を証明したいんだ? 5-6-10RMSについてのお話でした。見た目にパターンがないんです。 Alexey Subbotin 2009.11.28 20:52 #127 IlyaA >> : 5-6-10のシグマがないのがポイントです。そのままでは、そうですが、テストが必要です。それでも普通かもしれません。 はまずあり得ない。正規分布は、自然界では通常、ある「大きな」確率変数が、ある方法で(しかし同一に)分布する多数の「小さな」確率変数の和であるとされています。その代表的なものがブラウン運動で、すでに次のスレッドで多くのページが費やされています。なぜなら、正常なものを得るためには、非常に多くの外的な「擾乱」が必要であり、それが流通の形成の主因となるに違いないからである。市場の場合、価格形成の法則はそれとはかけ離れている。しかし、市場における価格設定がノイズであるとは考えていませんね。 Sceptic Philozoff 2009.11.28 20:52 #128 チャート上で、純粋に視覚的に、その5-6-10を見ることはできません。 どこかに、その違いを示す表も持っていた。分布の最初の2つのモーメントをとって、正規に近似するモーメントと考えれば、3、4、5などのシグマによる度数の差は簡単に計算できます。 正確な数値は覚えていませんが、実際の3シグマ偏差の頻度はガウス型の3〜4倍です(ガウス型0.3%、実質1%以上)。4シグマの偏差はガウス分布の偏差の約15倍、5シグマの場合は数十倍、数百倍の差がある。といった具合に。 リスクを評価しない限り、ガウスであろうがなかろうが関係ないのです。 追伸:ところで、Talebによれば、LTCMが破綻したのは、まさにリスクの過小評価によるものだったようです。10シグマの偏差は無視できるほどの希少事象とされた。そして、まさにそれが実現したのです。 Alexey Subbotin 2009.11.28 20:54 #129 Mathemat >> : 正確な数値は覚えていませんが、実際の3シグマ偏差の頻度はガウス型の3~4倍です(ガウス型0.3%、実質1%以上)。4シグマの偏差はガウス型偏差の約15倍、5シグマの場合は数十倍の差が現実に発生しています。といった具合に。 ...これはまた、ラプラスを支持する証拠となる。 ilyaa 2009.11.28 20:55 #130 Mathemat >> : リスクを評価しない限り、ガウスであろうがなかろうが関係ないのです。 リスクアセスメントへの取り組み方を教えてください。 1...678910111213141516171819 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
>> OKです。以下はそのデータです。お互いに誤解しているようです。私の異常に対する感情は、発電機ではなく、市場に適用されるものです。最初の増分の分布を構築して、自分の目で確かめてください。
真空中の球形の馬の場合、つまり正規分布が保証されている場合は、そうですね、ありえません。まあ、本物は真空中の馬ではありませんからね。5や6のS.C.E.もあれば、10のS.C.E.もあるんです。
おじさん、お願いします!今もう一枚、1971年のポンド、ダイアリーの写真です。ランジは1回かもしれませんが(ちなみに1回はないです : )、一番大事なのは、それがパターンにならないことです。そうだろ?
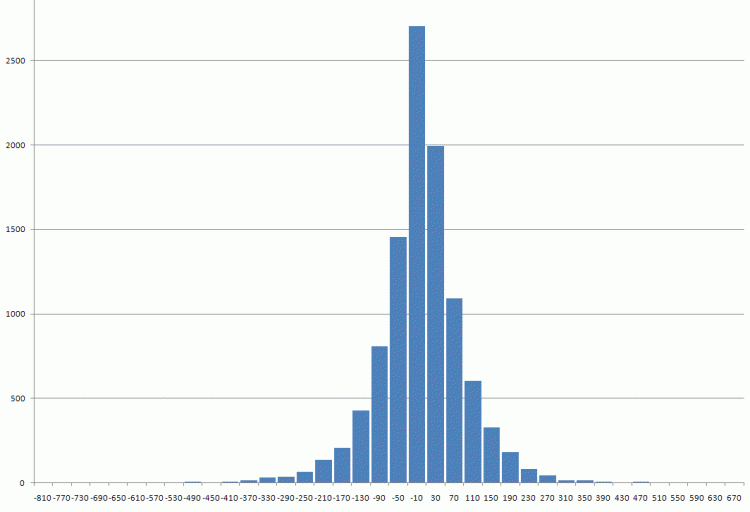
チェック用のデータを同封しています。1971年以来のポンド差。
>>S. 定常性のチェックを受けるべきかもしれません :)
おじさん、お願いします!今もう一枚、1971年のポンド、ダイアリーの写真です。ランジは1回かもしれませんが(ちなみに1回はないです : )、一番大事なのは、それがパターンにならないことです。そうだろ?
チェック用のデータを添付します。1971年以来のポンド差
目測でラプラス分布と言うところでしょうか。
目で見てラプラス分布と呼べるような
5-6-10のシグマがないのがポイントです。それ以外の場合は、そうですが、テストする必要があります。それでもいいのかもしれない。イリヤ ここで提案なんですが、この分布を正規分布で近似してみましょう。そして、実際のヒストグラムとガウス曲線の近似値がどれだけ違うかを確認します。3シグマにこだわらず、最低でも10シグマは調べましょう。
もう一つの簡単なチェックは、この分布の最初のモーメントを計算し、正規分布のモーメントと比較することです。
金融系列におけるファットテールという現象は古くから知られている。何を証明したいんだ?
イリヤ ここで提案なんですが、この分布を正規分布で近似してみましょう。そして、実際のヒストグラムとガウス曲線の近似値がどれだけ違うかを確認します。3シグマにこだわらず、最低でも10シグマは調べましょう。
もう一つの簡単なチェックは、この分布の最初のモーメントを計算し、正規分布のモーメントと比較することです。
金融系列におけるファットテールという現象は古くから知られている。何を証明したいんだ?
5-6-10RMSについてのお話でした。見た目にパターンがないんです。
5-6-10のシグマがないのがポイントです。そのままでは、そうですが、テストが必要です。それでも普通かもしれません。はまずあり得ない。正規分布は、自然界では通常、ある「大きな」確率変数が、ある方法で(しかし同一に)分布する多数の「小さな」確率変数の和であるとされています。その代表的なものがブラウン運動で、すでに次のスレッドで多くのページが費やされています。なぜなら、正常なものを得るためには、非常に多くの外的な「擾乱」が必要であり、それが流通の形成の主因となるに違いないからである。市場の場合、価格形成の法則はそれとはかけ離れている。しかし、市場における価格設定がノイズであるとは考えていませんね。
チャート上で、純粋に視覚的に、その5-6-10を見ることはできません。
どこかに、その違いを示す表も持っていた。分布の最初の2つのモーメントをとって、正規に近似するモーメントと考えれば、3、4、5などのシグマによる度数の差は簡単に計算できます。
正確な数値は覚えていませんが、実際の3シグマ偏差の頻度はガウス型の3〜4倍です(ガウス型0.3%、実質1%以上)。4シグマの偏差はガウス分布の偏差の約15倍、5シグマの場合は数十倍、数百倍の差がある。といった具合に。
リスクを評価しない限り、ガウスであろうがなかろうが関係ないのです。
追伸:ところで、Talebによれば、LTCMが破綻したのは、まさにリスクの過小評価によるものだったようです。10シグマの偏差は無視できるほどの希少事象とされた。そして、まさにそれが実現したのです。
正確な数値は覚えていませんが、実際の3シグマ偏差の頻度はガウス型の3~4倍です(ガウス型0.3%、実質1%以上)。4シグマの偏差はガウス型偏差の約15倍、5シグマの場合は数十倍の差が現実に発生しています。といった具合に。
...これはまた、ラプラスを支持する証拠となる。
リスクを評価しない限り、ガウスであろうがなかろうが関係ないのです。
リスクアセスメントへの取り組み方を教えてください。