ハーストの索引 - ページ 5 123456789101112...46 新しいコメント 削除済み 2007.01.13 12:51 #41 Yurixx: ハーストの計算方法は確かにいくつかありますが、grasnだけが 正しい計算方法を持っていると思い込むのは注意が必要です。実はそこには数学的な要素はあまりないので、どの方法も解明することができる。コードを取って、いろいろな列で実験すればいいんです。 対数比と直線近似のどちらを使うかが大きな問題です。 フェデラー以外は(特にピータース)、どこでも(Web論文で見つけた)対数比を使っている(しかも暗黙のうちに)。 議論では、ほぼ全員が直線に近似する必要があることを認識しているが。私は数学者ではなく、ただの読書家です :) だから、それはアッチ系の数学ではないんです...。 Yurixx 2007.01.14 00:20 #42 Gorillych писал (а): ユリックス。 ハーストの計算方法は確かにいくつかありますが、grasnだけが 正しい計算方法を持っていると思い込むのは注意が必要です。実はそこには数学的な要素はあまりないので、どの方法も解明することができます。コードを取って、いろいろな列で実験すればいいんです。 対数比と直線近似のどちらを使うかが大きな問題です。 フェデラー以外は(特にピータース)、どこでも(Web論文で見つけた)対数比を使っている(しかも暗黙のうちに)。 議論では、ほぼ全員が直線に近似する必要があることを認識しているが。私は数学者ではなく、ただの読書家です :) だから、それはアッチ系の数学ではないんです...。 Petersは、Hearstの指数=点群(Log(R/S),Log(N/2))にプロットした回帰直線の角度係数を求めています。 これらの対数の単純な比は、近似直線の角度係数ではなく、座標(Log(R/S),Log(N/2))の点の半径-ベクトルの角度係数を与えることになります。特にシーケンスのポイントが少ない場合、その差はかなりのものになります。 Shashev Sergei 2007.02.19 17:50 #43 ハーストのグラズン法による計算には触発されない。 . Hearst indexの幾何学的な意味は回帰直線の角度係数なので、この係数が反応速度によって変化するのは非常に不思議な気がする。そこで、ハースト社の指標をもとに、独自の指標を書くことにした。最初のバリエーションでは、いくつかの終値に基づいて 構築しましたが、すべてのシリーズを同時に基に指標を考える場合、結果は同じように見えますが、数バー速くなります。回帰線の角度係数が少しおかしいですが、すでに良くなっているように見えます:)一般的には、次のような指標があります。 ハーストレシオは、0.2~0.9の範囲にあります。スムーズに変動するのですが、変動するところがイマイチなんですよね。とはいえ、指標は全般的に面白いのですが)。 アルゴリズムは、ハーストの目利きのために以下に示されている。 。 for(int j=limit;j>=0;j--) { int max_index=ArrayMaximum(Close,HerstPeriod+j,j); int min_index=ArrayMinimum(Close,HerstPeriod+j,j); MaxH=Close[max_index]; MinH=Close[min_index]; R=MaxH-MinH; Average=iMA(NULL,0,HerstPeriod,0,0,0,j); sum=0; for (int i=1;i<=HerstPeriod;i++) sum+=MathPow((Average-Close[i+j]),2); double S=MathSqrt(sum/(HerstPeriod-1)); if (S>0) ExtMapBuffer1[j]=(MathLog(R/S))/(MathLog(HerstPeriod*a)); } 正しいようです。 ファイル: _hurst_classik.mq4 3 kb Shashev Sergei 2007.02.19 18:02 #44 その後、grasn さんがやろうとしたように、価格差に対してハースト指数を計算しました。価格系列は終値 系列とした。アルゴリズム for(int j=limit;j>=0;j--) { ExtMapBuffer2[j]=Close[j]-Close[j+1]; int max_index=ArrayMaximum(ExtMapBuffer2,HerstPeriod+j,j); int min_index=ArrayMinimum(ExtMapBuffer2,HerstPeriod+j,j); MaxH=ExtMapBuffer2[max_index]; MinH=ExtMapBuffer2[min_index]; R=MaxH-MinH; for (i=1;i<=HerstPeriod;i++) sum+=ExtMapBuffer2[i+j]; Average=sum/HerstPeriod; sum=0; for (i=1;i<=HerstPeriod;i++) sum+=MathPow((Average-ExtMapBuffer2[i+j]),2); double S=MathSqrt(sum/(HerstPeriod-1)); if (S>0) ExtMapBuffer1[j]=(MathLog(R/S))/(MathLog(HerstPeriod*a)); }は変わりません。唯一の違いは、一連の終値ではなく、その差で計算することです。結果は呆気ないものでした。 結果は、あるべき姿である0.5。本当にカオスなシリーズということですね!?そして、D1以下のすべての通貨と時間枠でこのように表示されます。日足では0.3~0.4である。持続性、つまり平均への回帰を意味します。指数計算の対象期間は500です。H1では約1ヶ月間です。 ハースト指標に基づく結論は、FXの価格系列はカオスで予測不可能であるということです :) もし私の計算が間違っていたら、訂正してください。 しかし、そのような結論を出すには、私はあまりに調査を怠ってきた。調査してくださる方 - 全部をブランチに投稿するか、favoritefx [woof-woof] mail.ruに送信してください。 ファイル: _hurst_delta.mq4 3 kb Иван 2007.02.19 19:03 #45 >>>為替相場はカオスであり、予測不可能である。 このスレッドでは、著者がFXにおけるカオス的な価格系列について研究しています。もし、私たちがFXで扱っていることに真剣に取り組もうと思われるのであれば、ご覧になってみてはいかがでしょうか。私見ですが、とても参考になります。 Сергей 2007.03.04 14:46 #46 皆さん、こんにちは。 私は完全に偶然にこのスレッドに来ました。ハーストの索引に関する私の研究が誰かの興味を引くものであることさえ知りませんでした。もしよろしければ、私のコメントを付け加えさせてください。中でも、私が挑戦してきたことは、すべてやり遂げました。https://www.mql5.com/ru/forum/50458 で示される指数の計算は、私は長い間使っていません。また、すべてを公開しているわけではなく、諸般の事情により公開しないことをご了承ください(公開する場合は、要約して公開する予定です)。 ハーストのバリューオールタイム0.5に関しては、トレーダーがすべての資金を節約できる優れた結果である。 一般的には、ハーストが現象を発見し、それを数値化したものがインデックス(彼の名前にちなんで命名)です。そして、これが最大のポイントですまた、0.5という結果は、非常に複雑なプロセスに対する一つの視点に過ぎません。簡単に説明すると、どのような動きを調査するかによります。ところで、あなたは何を研究し、ハーストに何を求めているのでしょうか?私が言うまでもないことだが、自分で決めなければならないことだ。 ハーストの数字が非常に滑らかなのは、計算ミスか、非常に大雑把な見積もりである。本来、超平滑にはできないのです。 ネット上のリンク先で見かける「簡単な計算」は、実はあまり正しくありません(間違っていると書いているわけではありません)。もう少し簡単な計算を加える必要があります。 自慢という意味ではなく、ハースト指数を使った私のモデルの結果ですが、 https://www.mql5.com/ru/forum/50458 "grasn 11.01.07 16:16"。もちろんフォーラムが「死なない」なら、近々続編を投稿するつもりです。 頑張ってください。 削除済み 2007.03.05 12:40 #47 grasn: 皆さん、こんにちは。 私は完全に偶然にこのスレッドに来ました。ハーストの索引に関する私の研究が誰かの興味を引くものであることさえ知りませんでした。もしよろしければ、私のコメントを付け加えさせてください。中でも、私が挑戦してきたことは、すべてやり遂げました。https://www.mql5.com/ru/forum/50458 で示される指数の計算は、私は長い間使っていません。また、すべてを公開しているわけではなく、諸般の事情により公開しないことをご了承ください(公開する場合は、要約して公開する予定です)。 こんにちは。 とてもうれしいです。あの支店で質問して、自分の無教養さをポイ捨てするのは気が引けました。 そのスレッドをじっくり読んで、今、少しでも何かを理解しようとしているところです。 セルゲイ版のハースト・インデックスが正しいと思う、とどこかで言っているのかもしれませんね。説明してください。 ありがとうございました。 がんばってください。 Сергей 2007.03.06 10:16 #48 Gorillych: グラサン 皆さん、こんにちは。 私は完全に偶然にこのスレッドに来ました。ハーストの索引に関する私の研究が誰かの興味を引くものであることさえ知りませんでした。もしよろしければ、私のコメントを付け加えさせてください。中でも、私が挑戦してきたことは、すべてやり遂げました。https://www.mql5.com/ru/forum/50458 で示される指数の計算は、私は長い間使っていません。また、すべてを公開しているわけではなく、諸般の事情により公開しないことをご了承ください(公開する場合は、要約して公開する予定です)。 こんにちは。 とてもうれしいです。あのスレッドで質問して、私の無知で散らかすのは不快でした。 そのスレッドを注意深く読み、今、少しでも何かを理解しようとしているところです。 セルゲイ版のハースト・インデックスが正しいと思う、とどこかでおっしゃったかもしれませんね。説明してください。 ありがとうございました。 がんばってください。 非常に自己批判的で、その通りだと思います。それが掲示板の目的であり、コミュニケーション、質問、議論などの場です。Sergeiが提案したHurst Indexの計算方法は、確かに非常に興味深い。こちらも合わせてご覧いただくことをお勧めします。 Vitali 2008.11.04 15:23 #49 favoritefx писал(а)>> その後、grasn さんがやろうとしたように、価格差に対してハースト指数を計算しました。価格系列として終値の系列がとられた。アルゴリズムそれは今も変わりません。唯一の違いは、終値の系列ではなく、その差で計算することです。その出来栄えは、まさに圧巻でした。 あるべき姿である0.5と出たのです。それが、このシリーズは本当にカオスなんですそして、D1以下のすべての通貨と時間枠でこのように表示されます。日足チャートで0.3~0.4です。持続性、つまり平均への回帰を意味します。指数計算の対象期間は500です。H1では約1ヶ月間です。 ハースト指標に基づく結論は、FXの価格系列はカオスで予測不可能であるということです :) もし私の計算が間違っていたら、訂正してください。 しかし、そのような結論を出すには、私はあまりに調査を怠ってきた。研究してくださる方は、このサイトに書き込むか、favoritefx [woof-woof]mail.ru まで送ってください。 ここはハーストじゃない。 ExtMapBuffer2[ j]=Close[ j]-Close[ j+1]; int max_index=ArrayMaximum( ExtMapBuffer2, HurstPeriod+ j-1, j); int min_index=ArrayMinimum( ExtMapBuffer2, HurstPeriod+ j-1, j); MaxH= ExtMapBuffer2[ max_index]; MinH= ExtMapBuffer2[ min_index]; コードからわかるように、最大値と最小値は元の系列に対して取られており、再スケーリングされた(スケーリングが変更された)系列に対しては取られていない。 さらにその先でも、エラーが発生しているようです。R/S=c*n^Hを 対数化すると、log(R/S)=log(c)+H*log(n),H=[log(R/S)-log(c)]/log(n) のような式になります。 ExtMapBuffer1[j]=(MathLog(R/S))/(MathLog(HurstPeriod*a)); 定数cが いつの間にかR/Sではなく nに 移動している。 なぜ、市場リターンの定数がいきなり2でなければならないのか。私が知らない秘密とは何だろう?;) とにかく、知恵遅れを助けてください、誰かmql4でハースト指数を計算したり、何か一般的なものを持っていませんか?グラサン? Metaquotes様、MQL5でハースト指数の計算は実装されるのでしょうか? Александр 2008.11.09 12:59 #50 ハーストは、ナイル川を研究しているときに経験則を発見した。その後、多くの自然現象がこの法則で記述できることが判明した。気温、河川流出量、降雨量、年輪の厚さ、波の高さなどの測定値の時間的な連続性は、正規化拡散法またはハースト法を用いて調べることができることがわかった。このような配列は、Hurst指数と呼ば れるH指数で特徴付けられる。 Hが0.5以上の時系列は、持続性(既存の傾向を維持する)のクラスに分類される。過去にある期間、増分がプラスであった場合、つまり増加があった場合は、平均して増え続けることになります。したがって、H>0.5のプロセスでは、過去に増加する傾向があれば、将来も増加する傾向があることを意味する。逆に言えば、過去に減少傾向があれば、平均して将来も減少傾向が続くということである。Hが大きいほど、その傾向は強くなる。 H=0.5では、有意なプロセストレンドはなく、将来的にあると考える根拠もない。 H < 0.5の場合、過去に成長すれば将来は減少し、過去に減少傾向であれば将来は増加する可能性が高いという、反存在的な特徴があります。そして、Hが小さいほど、その確率は高くなる。このようなプロセスでは、変数が増加した後は通常減少し、減少した後は通常増加する。 追記 ...興味のある方がいらっしゃいましたら 123456789101112...46 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
ハーストの計算方法は確かにいくつかありますが、grasnだけが 正しい計算方法を持っていると思い込むのは注意が必要です。実はそこには数学的な要素はあまりないので、どの方法も解明することができる。コードを取って、いろいろな列で実験すればいいんです。
フェデラー以外は(特にピータース)、どこでも(Web論文で見つけた)対数比を使っている(しかも暗黙のうちに)。 議論では、ほぼ全員が直線に近似する必要があることを認識しているが。私は数学者ではなく、ただの読書家です :)
だから、それはアッチ系の数学ではないんです...。
ハーストの計算方法は確かにいくつかありますが、grasnだけが 正しい計算方法を持っていると思い込むのは注意が必要です。実はそこには数学的な要素はあまりないので、どの方法も解明することができます。コードを取って、いろいろな列で実験すればいいんです。
フェデラー以外は(特にピータース)、どこでも(Web論文で見つけた)対数比を使っている(しかも暗黙のうちに)。 議論では、ほぼ全員が直線に近似する必要があることを認識しているが。私は数学者ではなく、ただの読書家です :)
だから、それはアッチ系の数学ではないんです...。
Petersは、Hearstの指数=点群(Log(R/S),Log(N/2))にプロットした回帰直線の角度係数を求めています。
これらの対数の単純な比は、近似直線の角度係数ではなく、座標(Log(R/S),Log(N/2))の点の半径-ベクトルの角度係数を与えることになります。特にシーケンスのポイントが少ない場合、その差はかなりのものになります。
. Hearst indexの幾何学的な意味は回帰直線の角度係数なので、この係数が反応速度によって変化するのは非常に不思議な気がする。そこで、ハースト社の指標をもとに、独自の指標を書くことにした。最初のバリエーションでは、いくつかの終値に基づいて 構築しましたが、すべてのシリーズを同時に基に指標を考える場合、結果は同じように見えますが、数バー速くなります。回帰線の角度係数が少しおかしいですが、すでに良くなっているように見えます:)一般的には、次のような指標があります。
ハーストレシオは、0.2~0.9の範囲にあります。スムーズに変動するのですが、変動するところがイマイチなんですよね。とはいえ、指標は全般的に面白いのですが)。
アルゴリズムは、ハーストの目利きのために以下に示されている。
。
正しいようです。
は変わりません。唯一の違いは、一連の終値ではなく、その差で計算することです。結果は呆気ないものでした。
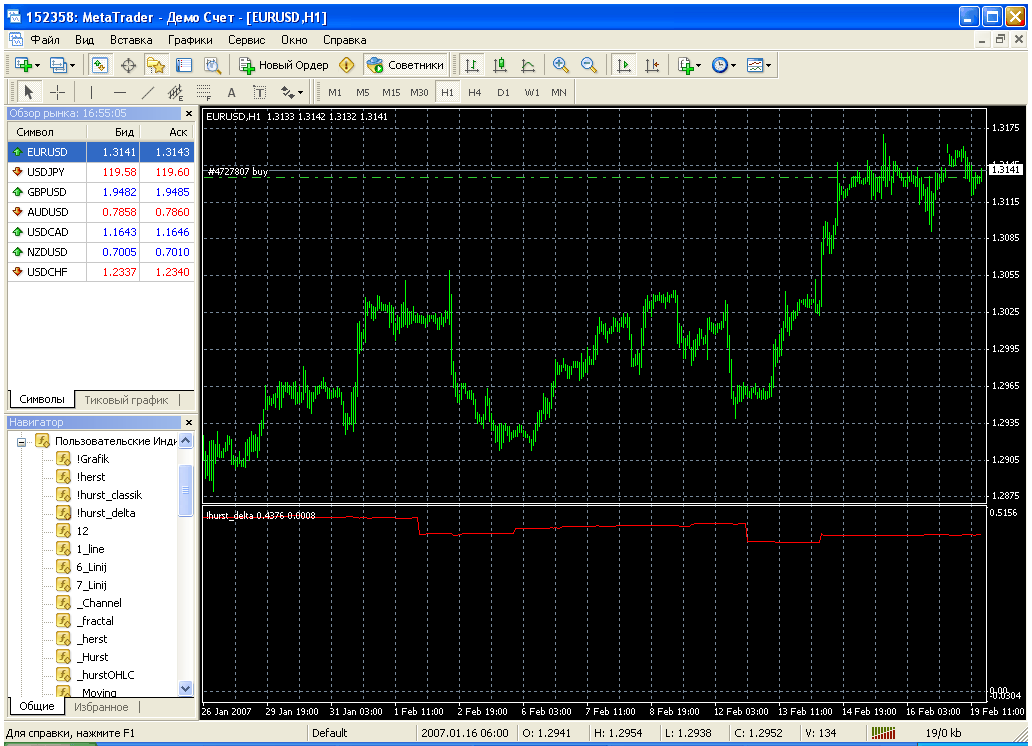
結果は、あるべき姿である0.5。本当にカオスなシリーズということですね!?そして、D1以下のすべての通貨と時間枠でこのように表示されます。日足では0.3~0.4である。持続性、つまり平均への回帰を意味します。指数計算の対象期間は500です。H1では約1ヶ月間です。
ハースト指標に基づく結論は、FXの価格系列はカオスで予測不可能であるということです :)
もし私の計算が間違っていたら、訂正してください。
しかし、そのような結論を出すには、私はあまりに調査を怠ってきた。調査してくださる方 - 全部をブランチに投稿するか、favoritefx [woof-woof] mail.ruに送信してください。
このスレッドでは、著者がFXにおけるカオス的な価格系列について研究しています。もし、私たちがFXで扱っていることに真剣に取り組もうと思われるのであれば、ご覧になってみてはいかがでしょうか。私見ですが、とても参考になります。
皆さん、こんにちは。
私は完全に偶然にこのスレッドに来ました。ハーストの索引に関する私の研究が誰かの興味を引くものであることさえ知りませんでした。もしよろしければ、私のコメントを付け加えさせてください。中でも、私が挑戦してきたことは、すべてやり遂げました。https://www.mql5.com/ru/forum/50458 で示される指数の計算は、私は長い間使っていません。また、すべてを公開しているわけではなく、諸般の事情により公開しないことをご了承ください(公開する場合は、要約して公開する予定です)。
ハーストのバリューオールタイム0.5に関しては、トレーダーがすべての資金を節約できる優れた結果である。
一般的には、ハーストが現象を発見し、それを数値化したものがインデックス(彼の名前にちなんで命名)です。そして、これが最大のポイントですまた、0.5という結果は、非常に複雑なプロセスに対する一つの視点に過ぎません。簡単に説明すると、どのような動きを調査するかによります。ところで、あなたは何を研究し、ハーストに何を求めているのでしょうか?私が言うまでもないことだが、自分で決めなければならないことだ。
ハーストの数字が非常に滑らかなのは、計算ミスか、非常に大雑把な見積もりである。本来、超平滑にはできないのです。
ネット上のリンク先で見かける「簡単な計算」は、実はあまり正しくありません(間違っていると書いているわけではありません)。もう少し簡単な計算を加える必要があります。
自慢という意味ではなく、ハースト指数を使った私のモデルの結果ですが、 https://www.mql5.com/ru/forum/50458 "grasn 11.01.07 16:16"。もちろんフォーラムが「死なない」なら、近々続編を投稿するつもりです。
頑張ってください。
皆さん、こんにちは。
私は完全に偶然にこのスレッドに来ました。ハーストの索引に関する私の研究が誰かの興味を引くものであることさえ知りませんでした。もしよろしければ、私のコメントを付け加えさせてください。中でも、私が挑戦してきたことは、すべてやり遂げました。https://www.mql5.com/ru/forum/50458 で示される指数の計算は、私は長い間使っていません。また、すべてを公開しているわけではなく、諸般の事情により公開しないことをご了承ください(公開する場合は、要約して公開する予定です)。
とてもうれしいです。あの支店で質問して、自分の無教養さをポイ捨てするのは気が引けました。
そのスレッドをじっくり読んで、今、少しでも何かを理解しようとしているところです。
セルゲイ版のハースト・インデックスが正しいと思う、とどこかで言っているのかもしれませんね。説明してください。
ありがとうございました。
がんばってください。
皆さん、こんにちは。
私は完全に偶然にこのスレッドに来ました。ハーストの索引に関する私の研究が誰かの興味を引くものであることさえ知りませんでした。もしよろしければ、私のコメントを付け加えさせてください。中でも、私が挑戦してきたことは、すべてやり遂げました。https://www.mql5.com/ru/forum/50458 で示される指数の計算は、私は長い間使っていません。また、すべてを公開しているわけではなく、諸般の事情により公開しないことをご了承ください(公開する場合は、要約して公開する予定です)。
とてもうれしいです。あのスレッドで質問して、私の無知で散らかすのは不快でした。
そのスレッドを注意深く読み、今、少しでも何かを理解しようとしているところです。
セルゲイ版のハースト・インデックスが正しいと思う、とどこかでおっしゃったかもしれませんね。説明してください。
ありがとうございました。
がんばってください。
その後、grasn さんがやろうとしたように、価格差に対してハースト指数を計算しました。価格系列として終値の系列がとられた。アルゴリズム
それは今も変わりません。唯一の違いは、終値の系列ではなく、その差で計算することです。その出来栄えは、まさに圧巻でした。
あるべき姿である0.5と出たのです。それが、このシリーズは本当にカオスなんですそして、D1以下のすべての通貨と時間枠でこのように表示されます。日足チャートで0.3~0.4です。持続性、つまり平均への回帰を意味します。指数計算の対象期間は500です。H1では約1ヶ月間です。
ハースト指標に基づく結論は、FXの価格系列はカオスで予測不可能であるということです :)
もし私の計算が間違っていたら、訂正してください。
しかし、そのような結論を出すには、私はあまりに調査を怠ってきた。研究してくださる方は、このサイトに書き込むか、favoritefx [woof-woof]mail.ru まで送ってください。
ここはハーストじゃない。
コードからわかるように、最大値と最小値は元の系列に対して取られており、再スケーリングされた(スケーリングが変更された)系列に対しては取られていない。
さらにその先でも、エラーが発生しているようです。R/S=c*n^Hを 対数化すると、log(R/S)=log(c)+H*log(n),H=[log(R/S)-log(c)]/log(n) のような式になります。
定数cが いつの間にかR/Sではなく nに 移動している。
なぜ、市場リターンの定数がいきなり2でなければならないのか。私が知らない秘密とは何だろう?;)
とにかく、知恵遅れを助けてください、誰かmql4でハースト指数を計算したり、何か一般的なものを持っていませんか?グラサン?
Metaquotes様、MQL5でハースト指数の計算は実装されるのでしょうか?
ハーストは、ナイル川を研究しているときに経験則を発見した。その後、多くの自然現象がこの法則で記述できることが判明した。気温、河川流出量、降雨量、年輪の厚さ、波の高さなどの測定値の時間的な連続性は、正規化拡散法またはハースト法を用いて調べることができることがわかった。このような配列は、Hurst指数と呼ば れるH指数で特徴付けられる。
Hが0.5以上の時系列は、持続性(既存の傾向を維持する)のクラスに分類される。過去にある期間、増分がプラスであった場合、つまり増加があった場合は、平均して増え続けることになります。したがって、H>0.5のプロセスでは、過去に増加する傾向があれば、将来も増加する傾向があることを意味する。逆に言えば、過去に減少傾向があれば、平均して将来も減少傾向が続くということである。Hが大きいほど、その傾向は強くなる。
H=0.5では、有意なプロセストレンドはなく、将来的にあると考える根拠もない。
H < 0.5の場合、過去に成長すれば将来は減少し、過去に減少傾向であれば将来は増加する可能性が高いという、反存在的な特徴があります。そして、Hが小さいほど、その確率は高くなる。このようなプロセスでは、変数が増加した後は通常減少し、減少した後は通常増加する。
追記 ...興味のある方がいらっしゃいましたら