[Matematica pura, fisica, chimica, ecc.: problemi di allenamento del cervello non legati in alcun modo al commercio - pagina 313
Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
P.S. Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1,2,4,8,16,32 - risposta singola
Se qualsiasi peso è inferiore a 2^n, il peso totale sarà inferiore a 63,
Se più, ci saranno lacune nella sequenza di pesi che si possono ottenere con questi kettlebells.
È interessante notare che il problema diventa notevolmente più difficile e interessante se i pesi possono essere posizionati su entrambe le tazze allo stesso tempo. Questo è quello che vorrei torturare. Ma non conosco la soluzione.
Anche se in ogni caso risulta che il peso minimo dei pesi è 1. Ma questo non significa automaticamente che vanno al grado 2.
Next (10°):
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Non sono sicuro del kettlebell minimo 1
forse anche due kettlebells 2 e 3 funzionerebbero.
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Il computer ha fatto i conti :)
Se i pesi possono essere messi simultaneamente su entrambe le tazze, il problema ha 2136 soluzioni (esattamente 63 pesi possono essere bilanciati).
Infatti, tutte le soluzioni contengono un peso di 1.
Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.
Pubblicherete il programma? Per favore, per favore!
Sì, chiedere in lacrime un programma.
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.
Mi sono sbagliato su 1.
Non c'è niente di interessante nel programma, un semplice overshoot.
#include <stdio.h>
#define COUNT 63
bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){
bool arr[COUNT];
for(int i=0;i<COUNT;i++) arr[i]=falso;
// 1 - su una tazza, 0 - il peso non è coinvolto -1 - sulla seconda tazza
for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
se(ves > COUNT) ritorna falso;
if(ves>0) arr[ves-1]=true;
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) restituisce false;
ritorna vero;
}
main(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if(isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d\n",i0,i1,i2,i3,i4,i5);
}
Следующая (10-й):
La prova è senza molto rigore, ma corretta.
Introduciamo la notazione delle coordinate dei vertici, come mostrato in figura. Perché il blu sia un quadrato
x1-x2=y1-y4 ;
y1-y2=x1-x2;
così come
x3-x4=y2-y3;
y4-y3=x2-x3.
Dalle prime due equazioni, se ricordiamo l'equazione del grafico, otteniamo
x4-x2=A(sinx2-sinx4),
dal terzo e quarto
x3-x1=A(sinx1-sinx3).
Dal momento che non viene imposta alcuna restrizione sui quadrati oltre al numero minimo di quadrati, considereremo solo i casi in cui i quadrati sono simmetrici rispetto all'origine. Ma allora x4=-x2, x3=-x1 e lo stesso con i seni. Le nostre equazioni avranno la forma:
sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A
Ricorda il grafico delle funzioni a partire da x2 e x1 che stanno sui lati sinistri. Per fare questo, guardate la figura: il grafico ha estremi decrescenti sia a x positivo che negativo. Ovviamente, riducendo gradualmente il numero A, possiamo ottenere tutte le radici di cui abbiamo bisogno, comprese 1978 e più.
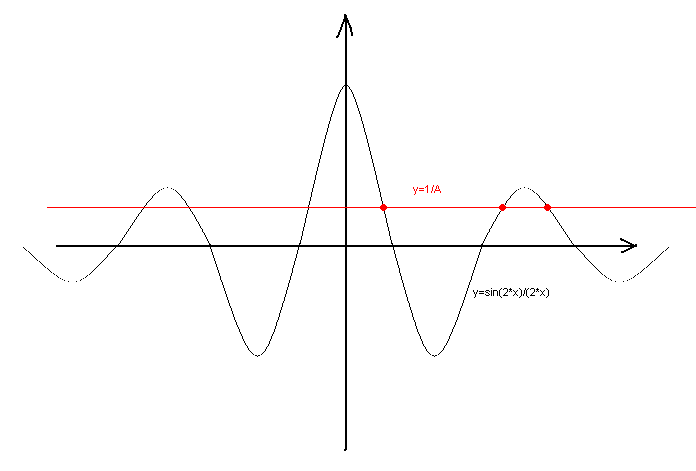
Le radici ottenute sono diverse, e si relazionano tra loro in modo puramente irrazionale. Non ho bisogno di dimostrare in dettaglio che i quadrati in questo caso non sono uguali a coppie.