Questo è fondamentalmente sbagliato.
In primo luogo, parliamo in russo e chiamiamo "curtosi" e "insularità" con il termine accettato - coefficiente di curtosi o semplicemente curtosi.
In secondo luogo, "insularità" e "code grasse" in generale non sono in alcun modo correlate. Ecco un controesempio: la distribuzione di Laplace ( esponenziale bilaterale), alla quale, va detto, obbediscono i grafici della stragrande maggioranza delle serie storiche finanziarie. Il suo eccesso è pari a 3 (cioè il suo vertice è più netto di quello della distribuzione normale), ma le code sono spesse - diminuiscono secondo la legge exp(-x), cioè più lentamente di quella della gaussiana exp(-x^2).
È fondamentalmente sbagliato.
In primo luogo, parliamo in russo e chiamiamo "curtosi" e "insularità" con il termine accettato - coefficiente di curtosi o semplicemente curtosi.
In secondo luogo, "insularità" e "code grasse" in generale non sono in alcun modo correlate. Ecco un controesempio: la distribuzione di Laplace (esponenziale bilaterale), alla quale, va detto, obbediscono i grafici della stragrande maggioranza delle serie storiche finanziarie. Il suo eccesso è pari a 3 (cioè la parte superiore è più netta che nella distribuzione normale), ma le code sono solo spesse - diminuiscono secondo la legge exp(-x), cioè più lentamente che nella gaussiana exp(-x^2).
Inoltre, non esiste un concetto di "eccesso" in sé, ma un concetto di "rapporto di eccesso", che è una misura per un altro concetto "eccesso di distribuzione", e questo concetto è definito solo per distribuzioni unimodali. Pertanto, per utilizzare correttamente questo coefficiente, è necessario, in primo luogo, determinare la funzione di distribuzione empirica, compito non banale dal punto di vista matematico, e in secondo luogo, nell'ambito di alcuni criteri probabilistici, verificare e accettare l'ipotesi che la distribuzione abbia un'unica modalità, cosa che non sempre si verifica per le serie finanziarie ed è anch'essa un compito non banale. Senza questi passaggi è impossibile effettuare ulteriori calcoli, se questi richiedono il "coefficiente di eccesso".
P.S..
Non è scritto nulla su cosa fare se il test dice che la serie non è applicabile al modello ipotizzato.
Nulla viene detto sul perché e su quale base venga utilizzata una serie di cosiddetti "rendimenti" e non un'altra.
In pratica, la ragione principale per cui lavorare con i rendimenti degli asset è preferibile a lavorare con i prezzi diretti degli asset è che i rendimenti hanno proprietà statistiche più interessanti.
alsu:
...Parliamo russo e chiamiamo "curtosi" e "insularità" con il termine accettato - coefficiente di eccesso o semplicemente eccesso....
Mi è piaciuto soprattutto il fatto che alsu consideri le parole "coefficiente" ed "eccesso" come russe...
alsu:
In secondo luogo, "insularità" e "code grasse" non sono generalmente correlate. Ecco un controesempio: la distribuzione di Laplace (esponenziale bilaterale), alla quale, va notato, obbediscono i grafici della stragrande maggioranza delle serie storiche finanziarie. Il suo eccesso è pari a 3 (cioè la parte superiore è più netta che nella distribuzione normale), ma le code sono solo spesse - diminuiscono secondo la legge exp(-x), cioè più lentamente che nella gaussiana exp(-x^2).
Questo è esattamente ciò che credo sia correlato in generale.
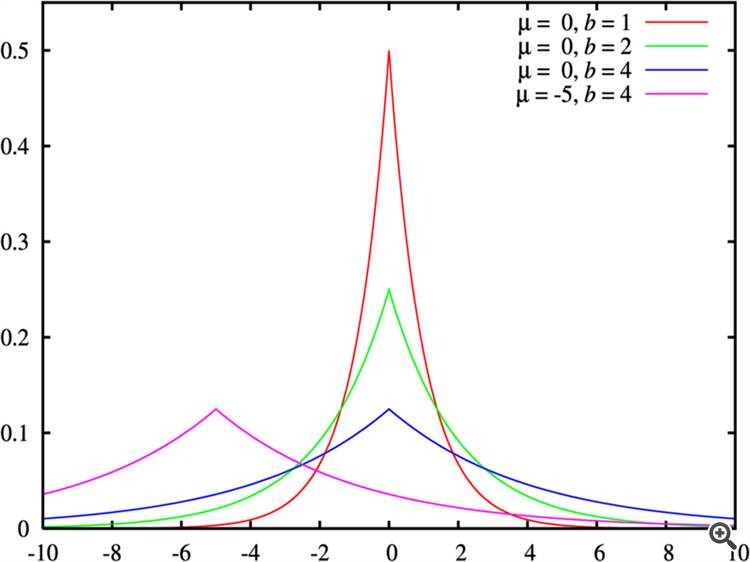
Un esempio di "coda meno curtosa e più spessa" è mostrato nella figura "Distribuzioni di Laplace con parametri diversi".
Aggiungerei solo la seguente frase al mio articolo: "La distribuzione di una serie di rendimenti presenta più spesso un comportamento a coda grassa rispetto alla distribuzione normale". Il fenomeno delle "code grasse" è chiamato eccesso di curtosi nella letteratura in lingua inglese. Le serie le cui distribuzioni presentano tali code sono dette leptocurtiche, avendo una curtosi positiva (superiore alla curtosi della distribuzione normale).
Poi il coefficiente di curtosi:
Ladistribuzione normale ha una curtosi pari a zero, γ2 = 0.
Se le code della distribuzione sono più "leggere" e il picco è più netto rispetto alla distribuzione normale, allora γ2 > 0. Se le code della distribuzione sono più "leggere" e il picco è più netto rispetto alla distribuzione normale, allora γ2 > 0.
Se le code della distribuzione sono più "pesanti" e il picco è più "appiattito" rispetto alla distribuzione normale, allora γ2 < 0.
Aggiungerei solo un suggerimento di questo tipo al mio articolo:
Aggiungerei solo la seguente frase al mio articolo: "La distribuzione di una serie di rendimenti presenta più spesso un comportamento a coda grassa rispetto alla distribuzione normale". Il fenomeno delle "code grasse" è chiamato eccesso di curtosi nella letteratura in lingua inglese. Le serie le cui distribuzioni presentano tali code sono dette leptocurtiche, avendo una curtosi positiva (superiore alla curtosi della distribuzione normale).
Poi il coefficiente di curtosi:
Ladistribuzione normale ha una curtosi pari a zero, γ2 = 0.
Se le code della distribuzione sono più "leggere" e il picco è più netto rispetto alla distribuzione normale, allora γ2 > 0. Se le code della distribuzione sono più "leggere" e il picco è più netto rispetto alla distribuzione normale, allora γ2 > 0.
Se le code della distribuzione sono più "pesanti" e il picco è più "appiattito" della distribuzione normale, allora γ2 < 0.
Mentre voi discutete sui termini, io ho già costruito alcuni EA redditizi utilizzando le idee di questo articolo. :-)
Tuttavia, i loro profitti sono molto piccoli, anche se sono abbastanza stabili (controllati sulla storia di 12 anni, i grafici crescono magnificamente). Le correlazioni rilevate dai metodi descritti nell'articolo sono piuttosto deboli ( i coefficienti di autocorrelazione delle serie sono di circa 0,01, in casi eccezionali si avvicinano a 0,1, a seconda dei derivati di prezzo correlati), e quando si fa trading il profitto è fortemente battuto dallo spread. Ho dovuto aggiungere un filtro per effettuare operazioni solo all'arrivo di segnali forti, altrimenti la curva di redditività sarebbe scesa quasi rettilinea.
Grazie all'autore in ogni caso. Le idee sono preziose. Ritengo che i critici non dovrebbero ficcare il naso negli abissi della matematica, ma considerare l'articolo come un'indicazione di un ampio campo per esperimenti pratici.
Mentre voi discutete sui termini, io ho già costruito alcuni EA redditizi utilizzando le idee di questo articolo. :-)
Tuttavia, i loro profitti sono molto piccoli, anche se sono abbastanza stabili (controllati sulla storia di 12 anni, i grafici crescono magnificamente). Le correlazioni rilevate dai metodi descritti nell'articolo sono piuttosto deboli (i coefficienti di autocorrelazione delle serie sono di circa 0,01, in casi eccezionali si avvicinano a 0,1, a seconda dei derivati di prezzo correlati), e quando si fa trading il profitto è fortemente battuto dallo spread. Ho dovuto aggiungere un filtro per effettuare operazioni solo all'arrivo di segnali forti, altrimenti la curva di redditività sarebbe scesa quasi rettilinea.
Grazie all'autore in ogni caso. Le idee sono preziose. Ritengo che i critici non debbano ficcare il naso negli abissi della matematizzazione, ma considerare l'articolo come un'indicazione di un ampio campo per esperimenti pratici.
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Il nuovo articolo Approccio econometrico all'analisi dei grafici è stato pubblicato:
Questo articolo descrive in particolare i metodi econometrici di analisi, l'analisi di autocorrelazione e l'analisi della varianza condizionale. Qual è il vantaggio dell'approccio qui descritto? L'uso dei modelli GARCH non lineari consente di rappresentare formalmente la serie analizzata dal punto di vista matematico e di creare una previsione per un numero specificato di passaggi.
È ovvio che l'oggettodell'analisi è una serie di prezzi (i suoi derivati), che è una serie temporale .
Gli econometristi studiano le serie temporali dal punto di frequenza ai metodi (analisi dello spettro, analisi wavelet) e ai metodi del dominio del tempo (analisi di correlazione incrociata, analisi di autocorrelazione). Al lettore è già stato fornito l'articolo "Building Spectrum Analysis" che descrive i metodi di frequenza. Ora suggerisco di dare un'occhiata ai metodi del dominio del tempo, all'analisi dell'autocorrelazione e all'analisi della varianza condizionale in particolare.
I modelli non lineari descrivono il comportamento delle serie temporali dei prezzi in modo migliore rispetto a quelli lineari. Ecco perché in questo articolo ci concentriamo sullo studio di modelli non lineari.
Le serie temporali dei prezzi hanno caratteristiche speciali che possono essere prese in considerazione solo da alcuni modelli econometrici. Prima di tutto, tali caratteristiche includono: "fat tail", clusterizzazione della volatilità ed effetto leva.
Autore: Denis Kirichenko