Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Oui
Malheureusement, je ne suis pas un mathématicien.Tout ce que tu dois savoir, c'est le cours d'algèbre de 8e année. Il n'est pas nécessaire d'être un mathématicien pour le faire.
La distance est marquée d -- voir comment elle est calculée.
Pourquoi c'est de la merde ? Pourquoi c'est de la merde ?
Parce que si vous reproduisez littéralement le code, vous obtenez un non-sens qui sera différent sur tous les graphiques.
Vous ne pouvez pas mesurer des angles dans un système de coordonnées qui change constamment. Votre angle de vue changera également.
En fait, vous devriez nous dire pourquoi vous en avez besoin, peut-être que tout le monde utilise déjà une autre solution pour votre problème.
pour comprendre ce dont nous parlons :
..................................................................
..................................................................
Vos images montrent tous les points d'intersection, mais en fait l'auteur ne dispose d'aucune donnée de coordonnées pour les points d'intersection avec la deuxième ligne. Les photos ne montrent pas clairement comment vous l'avez trouvé.
En fait, vous devriez dire pourquoi vous en avez besoin, peut-être que tout le monde utilise déjà une solution différente pour votre problème.
J'ai besoin de connaître la différence entre deux lignes parallèles...
La ligne rouge est la distance entre les lignes
jusqu'à présent, c'est de la théorie - http://www.cleverstudents.ru/line_and_plane/distance_between_parallel_lines.html mais comment le faire en pratique ?Dans vos images tous les points d'intersection sont connus partout, mais en fait l'auteur n'a pas les coordonnées des points de contact avec la deuxième ligne. Les photos ne montrent pas clairement comment vous l'avez trouvé.
Les images montrent l'ensemble du processus de résolution du problème, y compris la détermination des points d'intersection.
Oleg avtomat2018.03.31 04:30#37
Les images montrent l'ensemble du processus de résolution du problème, y compris la définition des points d'intersection.
Oleg avtomat2018.03.31 04:30#37
En regardant attentivement l'image (matlab apparemment ?)
En émettant une hypothèse, nous voyons deux fonctions où :
- "b" est le décalage de l'axe des y,
- "a" est le facteur de pente,
- "t" est la coordonnée de l'axe des x.
- "z(t)" est la nouvelle fonction qui décrit la perpendiculaire
n'est-ce pas ?
Je regarde plus loin et je n'arrive pas à comprendre, les expressions suivantes montrent quoi - où sont les flèches et l'inscription "solve" ?
Ensuite apparaît "r" (côté du triangle ?) - qu'est-ce que c'est et qu'implique la formule par les mots - degré ?
Ensuite, vous trouvez d, qui est une sorte de formule bien connue...
En regardant attentivement la figure (matlab apparemment ?)
Je pose une hypothèse, on voit deux fonctions, où :
- "b" est le décalage de l'axe des y,
- "a" est le facteur de pente,
- "t" est la coordonnée de l'axe des x.
- "z(t)" est la nouvelle fonction qui décrit la perpendiculaire
n'est-ce pas ?
Je regarde plus loin et je n'arrive pas à comprendre, les expressions suivantes montrent quoi - où sont les flèches et l'inscription "solve" ?
Ensuite apparaît "r" (côté du triangle ?) - qu'est-ce que c'est et qu'implique la formule par les mots - degré ?
Ensuite, vous trouvez déjà d, en quelque sorte par la formule que tout le monde connaît...
matcad
droite
"solve" = "solve" -- trouver le point d'intersection de la droite avec la perpendiculaire, c'est-à-dire trouver la valeur de t à laquelle y(t)=z(t)
substituer le t trouvé et déterminer r=y(t) à ce t particulier
Ainsi, nous obtenons les coordonnées de l'intersection (t;r) pour la première ligne
pour la deuxième ligne, effectuez les mêmes actions
comme résultat, nous avons deux points, dont la distance doit être déterminée
déterminer d par la formule
matcad
droite
"solve" = "solve" -- trouver le point d'intersection de la droite avec la perpendiculaire, c'est-à-dire trouver la valeur de t à laquelle y(t)=z(t)
Prends ton temps, ça veut dire résoudre, aha, mais ce n'est pas clair comment résoudre. Je le fais passer par un système d'équations ?
Prendre son temps, ça veut dire le résoudre, oui, mais ce n'est pas clair comment le résoudre. Je le fais passer par un système d'équations ?
Comme vous voulez.
vous pouvez le faire numériquement, avec une marge d'erreur acceptable - cela n'a pas d'importance.
Mais dans ce cas, c'est très simple à résoudre analytiquement.
je vous rappelle qu'un nombre infini de perpendiculaires peuvent être tracées à deux lignes parallèles données et que n'importe laquelle d'entre elles peut être utilisée pour déterminer la distance
en particulier est aussi une perpendiculaire aux lignes données :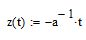
en assimilant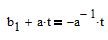
nous trouvons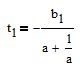
substituons cette valeur dans l'équation de la ligne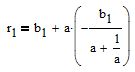
on obtient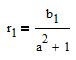
On trouve le premier point (t1;r1) et on détermine le second de la même manière.
Comme on peut le voir, il n'y a rien de compliqué. Il suffit de réfléchir un peu.