Je n'arrive pas à m'y retrouver dans le labyrinthe du code, mais j'aimerais le comparer.
Devis initial
Nous disposons des variantes de lissage suivantes :
Résultat du lissage
Équation de régression :
eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)
Estimation de l'équation de régression
| Variable | Coefficient | Stand.osh. | t-statistique | probabilité |
| EURUSDSM(-1) | 0.759607 | 0.049127 | 15.46225 | 0.0000 |
| REND | 0.000207 | 5.79E-05 | 3.577804 | 0.0005 |
| C | 0.314884 | 0.065276 | 4.823886 | 0.0000 |
R au carré = 0,788273
Erreur standard de la régression = 0,015172
Les chiffres obtenus permettent de constater que
tous les coefficients de régression sont significatifs (la probabilité qu'ils soient égaux à zéro est égale à zéro)
un R-carré assez élevé (mais pas très élevé), qui indique que la régression explique 78% de la variance
l'erreur standard est de 151 pips. C'est un chiffre énorme.
Peut-on se fier aux chiffres obtenus ?
Je ne le ferais pas, car selon Jarque-Bera, la probabilité que la série lissée ait une distribution normale est de 31 %.
Faisons une prévision :
L'erreur de prévision n'est pas loin de l'erreur de régression et dépasse 100 pips
Regardons le graphique de l'erreur de prévision :
Eh bien, c'est la fin complète : l'erreur est variable, ce qui signifie que le comportement futur de la prévision est inconnu !
Pour en trouver la raison, regardons la corrélation des coefficients de l'équation de régression :
Nous pouvons considérer que les coefficients c(1) et c(3) sont corrélés à près de 100 %.
Ma conclusion est que nous ne pouvons pas utiliser le lissage exponentiel pour la prédiction.
Pourquoi avons-nous des résultats différents ?
Il me semble évident que les paramètres optimaux que vous avez trouvés ne sont rien d'autre qu'un ajustement trivial. La régression elle-même est sans espoir, ses coefficients sont corrélés.
Il me semble évident que les paramètres optimaux que vous avez trouvés ne sont rien d'autre qu'un ajustement trivial. La régression elle-même est sans espoir, les coefficients étant corrélés.
Je vous remercie de l'intérêt que vous portez à l'article.
Veuillez préciser ce que vous voulez dire. Quels sont les résultats qui ne convergent pas et quels sont les paramètres optimaux ?
Veuillez préciser ce que vous entendez par là ?
Excusez-moi, vous dites que vous pouvez l'utiliser, mais j'en conclus que non.
Que faut-il utiliser et pourquoi ?
En conclusion, il convient de noter que les modèles de lissage exponentiel sont capables, dans certains cas, de produire des prévisions aussi précises que celles obtenues à l'aide de modèles plus complexes, ce qui confirme une fois de plus le fait que le modèle le plus complexe n'est pas toujours le meilleur.
Ma conclusion est que le lissage exponentiel ne devrait pas être utilisé pour les prévisions.
Sur quoi portent vos questions et pourquoi les posez-vous ?
Ma conclusion est que vous ne pouvez pas utiliser le lissage exponentiel pour les prévisions.
Sur quoi portent vos questions et à quoi servent-elles ?
J'aimerais bien essayer de répondre à quelque chose, mais je dois au moins connaître la question. Sinon, je ne ferai que deviner et fantasmer.
Je vais essayer de clarifier à nouveau.
Les modèles de lissage exponentiel ne peuvent pas être utilisés pour prévoir la paire eurusd, des citations ou jamais ?
P.S..
Vous avez dans votre texte : "Regression equation :eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)". Pourquoi une régression, alors que l'article traite des modèles de lissage exponentiel, et qu'il existe un modèle différent, à la place de c(3) il y a une variable aléatoire avec une certaine distribution et une certaine dispersion ?
Dans votre texte : "équation de régression :eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)". Pourquoi la régression, l'article traite des modèles de lissage exponentiel, et il y a un modèle différent, où au lieu de c(3) il y a une variable aléatoire avec une certaine distribution et variance ?
Cela ne marche pas, on parle d'un aveugle à un sourd. Remettons cela à plus tard.
Félicitations encore pour ce bon article.
Cela ne fonctionne pas, parler d'un aveugle à un sourd. Remettons cela à plus tard.
Je vous félicite à nouveau pour ce bon article.
Je suis en fait très curieux de connaître votre point de vue sur les prévisions utilisant le lissage exponentiel. Il y a beaucoup de choses que je ne sais pas et je suis toujours heureux d'essayer de découvrir quelque chose de nouveau à chaque occasion, c'est pourquoi je pose des questions.
Si cela ne vous dérange pas trop, expliquez-moi pourquoi, si la distribution de la séquence originale (ou de la séquence originale lissée) n'est pas normale, la prévision n'est pas fiable ? Ou vous ai-je mal compris ?
Merci pour vos félicitations.
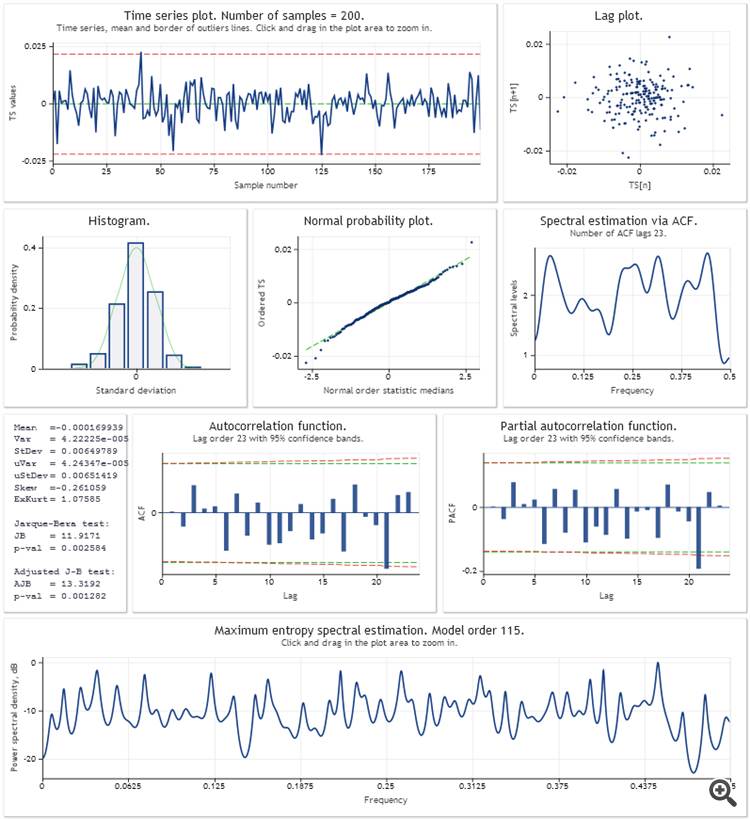
Voici une analyse de l'erreur de prédiction à un pas en avant pour le modèle de croissance linéaire additif avec amortissement. Les paramètres du modèle ont été optimisés en utilisant un échantillon des 200 dernières valeurs de USDJPY,M1. De la même manière que dans le script Optimisation_Test.mq5 de l'article.
https:// www.mql5.com/ru/articles/292
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Un nouvel article Prévision de Séries Chronologiques à l'Aide du Lissage Exponentiel a été publié :
L'article familiarise le lecteur avec les modèles de lissage exponentiel utilisés dans la prévision à court terme des séries chronologiques. De plus, il aborde les questions liées à l'optimisation et à l'estimation des résultats prévisionnels et fournit quelques exemples de scripts et d'indicateurs. Cet article sera utile pour une première prise de connaissance des principes de prévision à partir de modèles de lissage exponentiel.
Il convient de noter que le même coefficient alpha est utilisé dans les formules ci-dessus pour le premier lissage et le lissage répété. Ce modèle est appelé modèle additif à un paramètre de croissance linéaire.
Expliquons la différence entre le modèle simple et le modèle de croissance linéaire.
Admettons que pendant longtemps le processus à l'étude ait représenté un composant constant, c'est-à-dire qu'il apparaisse sur le graphique sous la forme d'une ligne droite horizontale mais qu'à un moment donné une tendance linéaire commence à émerger. Une prévision de ce processus réalisée à l'aide des modèles mentionnés ci-dessus est illustrée en figure 2.
Figure 2. Comparaison de modèles
Auteur : Victor