Discusión sobre el artículo "Características del Wizard MQL5 que debe conocer (Parte 02): Mapas de Kohonen"
Queda una duda, como podemos entender porque se toma el valor de IN_RADIUS modulo para normalizar los datos:
double _dimension=fabs(IN_RADIUS)*((Low(StartIndex()+w+Index)-Low(StartIndex()+w+Index+1))-(High(StartIndex()+w+Index)-High(StartIndex()+w+Index+1))))/fmax(m_symbol.Point(),fmax(High(StartIndex()+w+Index),High(StartIndex()+w+Index+1))-fmin(Low(StartIndex()+w+Index),Low(StartIndex()+w+Index+1))));
porque el radio del cluster es una constante y tiene un valor positivo.
¿Tal vez se trate de un error y deba tomarse todo el numerador como módulo?
He montado el Asesor Experto, pero dos parámetros Stop Loss y Take Profit no son los mismos que en la captura de pantalla en el artículo:
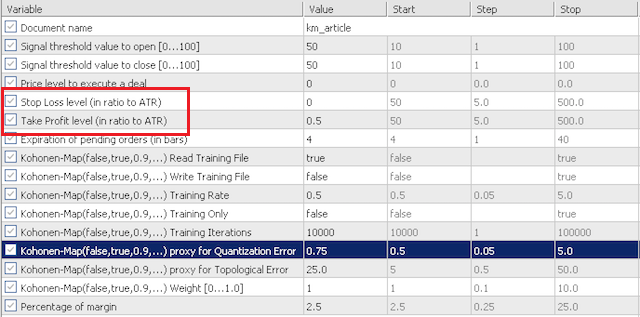
Como resultado, ni un solo comercio ...
¿Estoy haciendo algo mal?
¿Y cómo utilizar otro indicador en lugar de ATR, por ejemplo MACD?
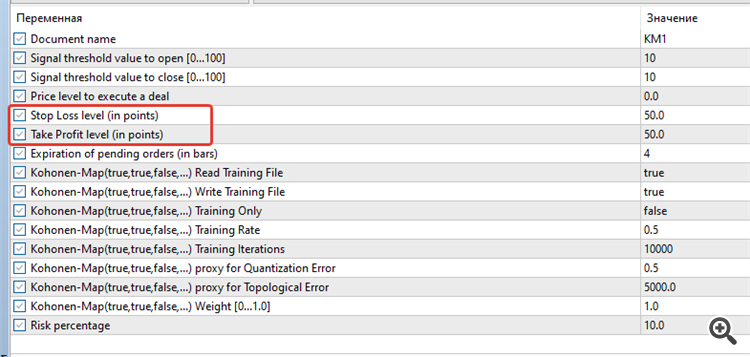
Construí el Asesor Experto, pero dos parámetros Stop Loss y Take Profit no son los mismos que en la captura de pantalla en el artículo:
Como resultado, ni un solo comercio ...
¿Estoy haciendo algo mal?
¿Y cómo utilizar otro indicador en lugar de ATR, por ejemplo MACD ?
Se puede hacer de esta manera:
bool CSignalMACD::InitMACD(CIndicators *indicators) { //--- añadir objeto a la colección if(!indicators.Add(GetPointer(m_MACD))) { printf(__FUNCTION__+": error adding object"); return(false); } //--- inicializar objeto if(!m_MACD.Create(m_symbol.Name(),m_period,m_period_fast,m_period_slow,m_period_signal,m_applied)) { printf(__FUNCTION__+": error initializing object"); return(false); } //--- ok return(true); }
también en protegido:
protected: CiMACD m_MACD; // objeto-oscilador //--- parámetros ajustados int m_period_fast; // el parámetro "periodo de EMA rápida" del oscilador int m_period_slow; // el parámetro "periodo de EMA lenta" del oscilador int m_period_signal; // el parámetro "periodo de promediación de la diferencia" del oscilador ENUM_APPLIED_PRICE m_applied; // el parámetro "serie de precios" del oscilador
y en público:
void PeriodFast(int value) { m_period_fast=value; } void PeriodSlow(int value) { m_period_slow=value; } void PeriodSignal(int value) { m_period_signal=value; } void Applied(ENUM_APPLIED_PRICE value) { m_applied=value;
y de nuevo en protected
protected: //--- método de inicialización del oscilador bool InitMACD(CIndicators *indicators); //--- métodos de obtención de datos double Main(int ind) { return(m_MACD.Main(ind)); } double Signal(int ind) { return(m_MACD.Signal(ind)); }
y finalmente:
bool CSignalKM::OpenLongParams(double &price,double &sl,double &tp,datetime &expiration) { CExpertSignal *general=(m_general!=-1) ? m_filters.At(m_general) : NULL; //--- if(general==NULL) { m_MACD.Refresh(-1); //--- si no se especifica explícitamente un precio base, toma el precio de mercado actual double base_price=(m_base_price==0.0) ? m_symbol.Ask() : m_base_price; //--- sobrecarga de precio que establece que el precio de entrada se base en el MACD price =base_price; double _range=m_MACD.Main(StartIndex())+((m_symbol.StopsLevel()+m_symbol.FreezeLevel())*m_symbol.Point()); //
¿Pero qué sentido tiene?
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Características del Wizard MQL5 que debe conocer (Parte 02): Mapas de Kohonen:
Gracias al Wizard, el tráder podrá ahorrar tiempo a la hora de poner en práctica sus ideas. Asimismo, podrá reducir la probabilidad de que surjan errores por duplicación de código. En lugar de perder el tiempo con el código, los tráders tendrán la posibilidad de poner en práctica su filosofía comercial.
Un concepto erróneo común sobre los mapas de Kohonen es que los datos funtoriales deben ser una imagen 2D como la que se muestra a continuación.
Esta interpretación tiene derecho a existir, pero cuando se aplica al trading, el functor puede (y, quizás, debería) tener una dimensión. Por lo tanto, en lugar de reducir nuestros datos multidimensionales a un mapa bidimensional, los trazaremos en una sola línea. Por definición, los mapas de Kohonen están diseñados para reducir la dimensionalidad. En el presente artículo, aprovecharemos esta función y la llevaremos al siguiente nivel. Los mapas de Kohonen se diferencian de las redes neuronales convencionales tanto en el número de capas como en el algoritmo subyacente.
Se trata de un conjunto de una sola capa de neuronas, generalmente realizado en forma de cuadrícula bidimensional lineal. Todas las neuronas de esta capa, a la que llamamos funtor, se conectan a los datos originales,pero no entre sí.. Esto significa que las neuronas no dependerán del peso de las demás directamente y se actualizarán solo cuando cambien los datos de origen. La capa de datos del funtor es un "mapa"que se autoorganizará en cada iteración de entrenamiento según los datos de entrada. Por consiguiente, después del entrenamiento, cada neurona tendrá un tamaño ajustado al peso en la capa del funtor, y esto permitirá el cálculo de la distancia euclidiana entre dos de estas neuronas.
Autor: Stephen Njuki