You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
Contact via private message, find out about the conditions.
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
Are the indicators paid or something? Published in the codebase, use it to your heart's content!
New article Universal Regression Model for Market Price Prediction is published:
Author: Юсуфходжа
good article.
very impressive
It is a pity, but there are mistakes at the very beginning of the article.
Firstly, the price increment at some time t will of course have some value and we denote it by D0. Let's assume.
Next... Now at t=0, I understand that there is no impact on the price and apparently there is no price increment from the external impact either. However, we again called the delta D0.
Then we put dt/tau into the formula, which is 1/C^2 anyway, i.e. we gave acceleration to the impact, which will move the geometric regression anyway. Why should we? After all, we have not yet defined - what this impact is such...
well, in general.
It is a pity, but there are mistakes at the very beginning of the article.
Firstly, the price increment at some time t will of course have some value and we denote it by D0. Let's assume.
Next... Now at t=0, I understand that there is no impact on the price and apparently there is no price increment from the external impact either. However, we again called the delta D0.
Then we put dt/tau into the formula, which is 1/C^2 anyway, i.e. we gave acceleration to the impact, which will move the geometric regression anyway. Why should we? After all, we have not yet defined - what this impact is such...
well, in general...
1. Do is not the price increment, but the initial potential of the force affecting the price at time t=0.
2. from the article: ".... assume that the market price, which is in equilibrium, can change only under the action of some external force D(t), the magnitude and value of which we will measure in the same dimension as the price.
Let us also assume that the change in the market price P(t) with the passage of time t from the beginning of the influence of this force, continuously increasing from zero value by some regularity unknown to us yet, tends to reach the value P(∞) = D0 in infinity. That is, by D0 we mean a finite increment or decrease of the market price, depending on the nature and sign of this influencing force.
Moreover, we assume that D(t=0) = D0. Let us further assume that during the infinitesimal period of time dt the influencing force will decrease by the value dD(t) in proportion to the remaining force D(t) by the moment of time t:
whence we obtain the exponential dependence of D(t) on time t in the form:
Where: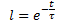
t - time from the beginning of the impact of destabilising force in time series units, sec. (min, hours, days, weeks, decades, months, years);
τ (tau) - the proportionality coefficient, numerically equal to the time constant of the process, sec.(min, hours, days, weeks, decades, months, years)."
Where did you find the dimensionality of 1/s^2 from? That ratio has no dimensionality. I didn't slip it in, I hypothesised that, the rate of change (decrease) of a force acting on a process is proportional to the force itself, which doesn't contradict logic, and then, this hypothesis was fully confirmed. As a coefficient of proportionality and introduced the ratio a (alpha) = 1/tau, which has the inverse of time, dimension. By a (alpha) I understand the impedance of the system, meaning the resistance of the system to the flow of the process, and tau is the image of time in Laplace transformations, as it turned out later, and allows to take the analysis of the process from the differential domain to the ordinary one. This means that any process has its own time, different from ours, and tau acts as a "translator" of times, if I may put it this way. In the bowels of the article I gave a way to estimate tau:
Now, if the values of the function f to the corresponding moments of time t are known, then from this equation the parameters n, τ and the coefficient β are determined as follows:
where:
The values of the function f to the corresponding moments of time t and time t are determined by the actual values of the market price P0, P1,..., Pk to the moments of time h0, h1,..., һk from the beginning of its destabilisation by numerical differentiation, referred to the middle of the interval:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); and so on;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; and so on.