Please consider which section is most appropriate — https://www.mql5.com/en/forum/172166/page6#comment_49114893
Well you are probably already using machine learning to improve a strategy with the strategy tester.
In general we dont know what the algorithm learns . If we take a neural network for instance and feed 100 bars as features with a buy/sell/sleep output at the end we dont know which patterns it is trading , what the similarity tolerance is if it is constructing an index (an indicator) inside the hidden layers etc.
[we also don't know if it sees some weird pattern that it has not encountered before and blow up the account]
So most times , unless you are tuning settings , you are searching for a new strategy .
For starters if you want to "improve" your strategy you can try one of the easiest to implement methods the "Random search"
you take a random step on both directions on all settings , measure if it is good or bad .
On each cycle you take 10 of those and you choose the best step to adjust your settings .
Then you repeat from that point .
You'll face the same issue a neural net deployment has though . The learning rate .
Imagine that picking the starting learning rate and managing how it fluctuates is the equivalent of scoring a 3 pointer from another stadium.
This is the worse aspect of ML . We think we'll buy a super pc with a 3 way SLI nvidia setup and the neural nets will magically work , where what happens is you just fail faster at tuning it.
[not to mention that if you want to test your own ML ideas the super pc is useless unless you know how to make your ideas run as fast as possible and in parallel , or until the people with that ability come up with the same ideas.]https://www.mql5.com/en/docs/matrix/matrix_machine_learning
You can try a simpler version first before jumping in matrices and vectors .
The main mechanism that is hard to grasp at first is the derivation .
And also the fact that all lectures and all examples and all tutorials that are detailed have one layer between the outputs and inputs.
The phrase you most often hear is the "partial derivative with respect to"
What that means is "we want to find what affects this variable"
For instance , in the "easy math" we understand y=3x , if i have the y (outout) and i want to find the x(weight) (which was randomly assigned) then i can do x=y/3 .
So we take the y result of a known case and divide it by 3 . Funny enough the derivative of y=3x with respect to x is 3 and the derivative of x=y/3 with respect to y (what we sent in as the known result) is 1/3.
In general :
When we move from left to right we multiply and sum and activate
When we move from right to left we subtract , derive and multiply. Subtraction happens once on the output layer.
The best exercise is to build the simplest neural net on your own using classes before jumping into matrix / vector stuff.
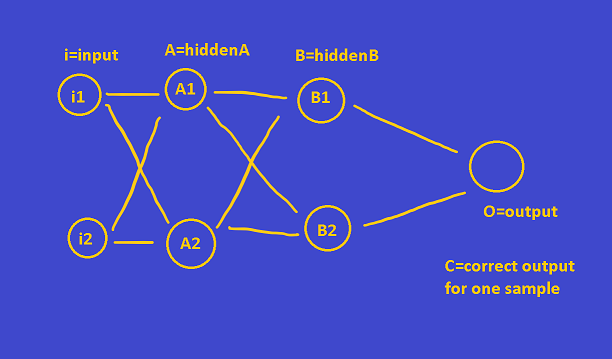
Lets assume this network for example
- For one sample , O has a value and the correct value is C :
- Subtract C from O (O means output its not a zero) , error=O-C
- That value though was produced by the activation function at O so multiply it with the derivative of that function , error*=deriv_O
- But then this value came in through the weights , so , each node connecting to O with weights has a responsibility for that error . How much responsibility ? weight much , error*=weight.
Now this is the first point tutors are fuzzy about because they use matrices in python .
Should you sum the error a node receives at each backpropagation ? YES . Why? because it may be connecting to multiple nodes on the next layer and some might be resulting in good outputs some in bad outputs so you need the net "responsibility" or the net pointed finger at this node . Guess what else this can do . At any time during training you know which node is responsible for most mistakes.
So to the example above . The error will split into 2 moving from the output layer and node O to B1 and B2 . the error that was error*=deriv_0 will become :
- additive to B1's error = error*=weight_B1_to_O
- additive to B2's error = error*=weight_B2_to_O
Then what happens , most tutorials and lectures stop here . You start the same process all over again for each node of the B layer but you dont subtract anything because you already have an error estimate for this node ! (calculated from the layers to its right)
So , how is the B1 value calculated ? The B1 activation . So , multiply the B1 error by the derivative of B1 . Then what is sending the values to B1 activation , the weights , send back the error (and split further) into the nodes of layer A . etc .
Now , how does it "learn" ?
In between sending the errors to the previous nodes we do a simple calculation to estimate what a more proper weight would be .
So now imagine this :
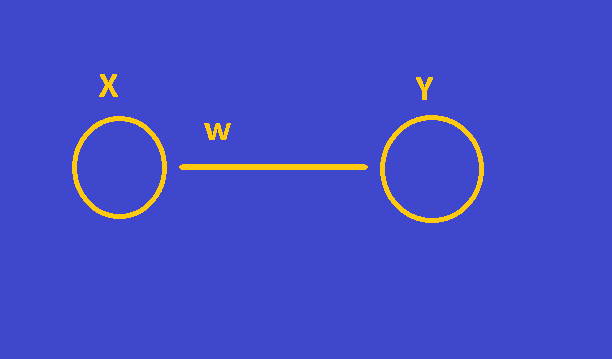
Imagine you are back propagating and you are at node Y . You have collected the error for node Y and you have multiplied the error (for node Y) by the derivative of its activation .
What do you have ? you are holding an adjustment value for the sum that came in the activation function of Y. or how "off" it was.
You need to "tune" w so that it results in error 0 .So the distance of the sum that comes into Y activation from it being correct (or error 0) is the error .
What is the w adjustment needed given we know X ? w_adj=X * errorY (errorY after multiplied with derivative Y) . And this w_adj will be multiplied by the learning rate and added to your weight for this connection.
That is it.
And you also see why learning rate is used .
If for instance you have a network and node A1 is responsible for the errors , but we dont know that , we cannot fully (or learning rate = 1.0) adjust all weights because we will correct node A1 but mess up all other nodes resulting in errors again . (or as they call it "overshoot")
That is it more or less .
Try and build a class based NN , you will understand many things .
Also keep in mind that machine learning is more math and biology than programming , unfortunately . So every idea under the sun has that "lingo"
So when you finish you class based network , you'll feel all the lessons you have watched were overcomplicating things (over to the power of 10).
And that's why python is dominating , it is the common language between coders and mathematicians.
Of course you are right. I completely forgot that I had to look into Matrix multiplication for weeks. *facepalm* If people are fresh out of college, they might get it quicker. But I found this very good explaination
And even booked a course on a renouned interactive app. Which did not yield the expected results, so I did not manage to put the knowledge into action because I haven't been able to extract what exactly the backprop really does... But this video is still the best I found on matrix multiplication. Which is basically how feedforward works.
Of course you are right. I completely forgot that I had to look into Matrix multiplication for weeks. *facepalm* If people are fresh out of college, they might get it quicker. But I found this very good explaination
And even booked a course on a renouned interactive app. Which did not yield the expected results, so I did not manage to put the knowledge into action because I haven't been able to extract what exactly the backprop really does... But this video is still the best I found on matrix multiplication. Which is basically how feedforward works.
It is telling you where the solution direction is .
But when you backpropagate it , i.e. when you send the "offshoot" (or the miss) you are getting the offshoot for all nodes . So you cant correct all nodes at once because you dont know which node is the "bad boy" , so you use a learning rate .If the node was not responsible , on the next stochastic step it's error will evaporate.
imagine for instance you have a drawing mechanism with angle and radius.
You draw a random angle and radius , then the system gives you the distance to your goal . What is wrong ? the angle or the radius ? Now imagine not 2 parameters (angle,radius) but 2 million . That's what backprop does . It facilitates the function approximation . i.e. mathematical coding.
PS . fix your editor metaquotes
It is telling you where the solution direction is .
But when you backpropagate it , i.e. when you send the "offshoot" (or the miss) you are getting the offshoot for all nodes . So you cant correct all nodes at once because you dont know which node is the "bad boy" , so you use a learning rate .If the node was not responsible , on the next stochastic step it's error will evaporate.
imagine for instance you have a drawing mechanism with angle and radius.
You draw a random angle and radius , then the system gives you the distance to your goal . What is wrong ? the angle or the radius ? Now imagine not 2 parameters (angle,radius) but 2 million . That's what backprop does . It facilitates the function approximation . i.e. mathematical coding.
PS . fix your editor metaquotes
I know I know. The abstract of what a backpropagation does is clear: It DOES the lerning. So far so good. My problem is the nitty-gritty and how the learning rate gets distributed along the weights between two layers IN DETAIL. If you could give me a course I would pay you on the hour. 🤓
The learning rate is a big headache.
It's something you have to figure out .
Why it's used : Because at first we don't know which layer/nodes are wrong since we started from a random state.
With backpropagation we essentially measure how wrong each node is , but , as you move to the right you can't be certain that a node is wrong because of the weights or the
activations it received (to sum).
Similarly with the first hidden layer nodes , you don't know if the error is due to all the weights or some of the weights .
That means if we use learning rate 1.0 we are changing the network by a lot .
We are correcting the weights that were wrong , but , we are messing up the weights that were right (because we assumed they were also wrong)
There is an optimizer that auto adjusts the learning rate , i'll find it and post it here .
AdaTune
https://github.com/awslabs/adatune
- awslabs
- github.com
Oh yes that was also my biggest headache that the biggest weights are changed the most but not always in the right direction I guess. The more you think about it the more counter intuitive it looks.
Yes , the truth is an explanation is difficult .
I mean the first natural thing that comes to mind is reversing the equation not deriving it.
But then you try that and see that theres a dimensionality increase that assists in approximating the "function"
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
I am trying to understand use causes of machine learning and neural networks as i am a novice in this field.
I want to know if there is a strategy with 20% accuracy can be improved by using machine learning or neural network up to 80%?
What are some good examples using MQL5 for very basic understanding of how these process works, as I am only looking to invest my time learning if it is beneficial for any research so just want to know the possibility and result from these. I have already read articles and watched videos on this topic but my purpose on forum post is to get some advice /feedback from experienced neural network / machine learning users to find out if by using it program can self learn profitable trading so has anyone achieved this using it?