[Archive!] Pure mathematics, physics, chemistry, etc.: brain-training problems not related to trade in any way - page 313
You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
P.S. Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1,2,4,8,16,32 - single answer
If any weight is less than 2^n, the total weight will be less than 63,
If more, there will be gaps in the sequence of weights that can be obtained with these kettlebells.
Interestingly, the problem becomes considerably more difficult and interesting if the weights can be placed on both cups at the same time. That's the one I'd like to torture. But I don't know the solution.
Although in any case it turns out that the minimum weight of the weights is 1. But this does not automatically mean that they go to the degree of 2.
Next (10th):
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
I'm not sure about the minimum kettlebell 1
maybe two kettlebells 2 and 3 would work too.
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
The computer has done the math :)
If the weights can be placed on both cups simultaneously, the problem has 2136 solutions (exactly 63 weights can be balanced).
Indeed, all the solutions contain a weight of 1.
Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.
Will you post the programme? Please, please!
Yep, tearfully ask for a program.
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.
I was wrong about 1.
There's nothing interesting in the programme, a simple overshoot.
#include <stdio.h>
#define COUNT 63
bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){
bool arr[COUNT];
for(int i=0;i<COUNT;i++) arr[i]=false;
// 1 - on one cup, 0 - weight is not involved -1 - on the second cup
for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if(ves > COUNT) return false;
if(ves>0) arr[ves-1]=true;
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) return false;
return true;
}
main(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if(isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d %d\n",i0,i1,i2,i3,i4,i5);
}
Следующая (10-й):
The proof is without much rigor, but correct.
Let us introduce the notation of vertex coordinates, as shown in the figure. For blue to be a square
x1-x2=y1-y4 ;
y1-y2=x1-x2;
as well as
x3-x4=y2-y3;
y4-y3=x2-x3.
From the first two equations, if we recall the graph equation, we get
x4-x2=A(sinx2-sinx4),
from the third and fourth
x3-x1=A(sinx1-sinx3).
Since no restrictions are imposed on the squares other than the minimum number of squares, we will consider only those cases where the squares are symmetric about the origin. But then x4=-x2, x3=-x1 and the same with sines. Our equations will take on the form:
sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A
Recall the graph of functions from x2 and x1 standing on the left-hand sides. To do this, look at the figure: the graph has decreasing extrema at both positive and negative x. Obviously, by gradually reducing the number A, we can obtain as many roots as we need, including 1978 and more.
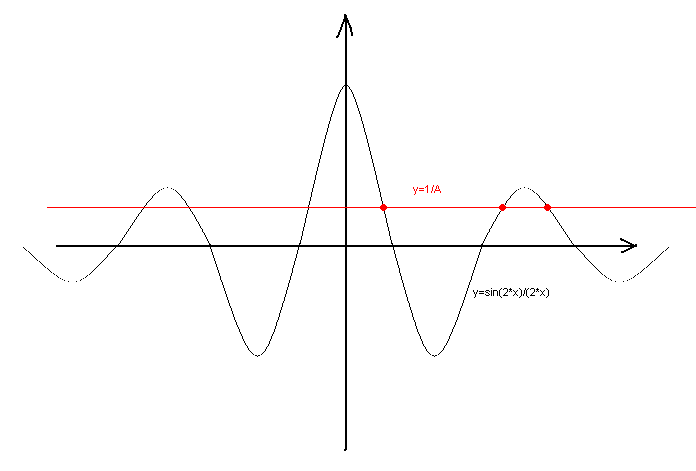
The obtained roots are different, and relate to each other in a purely irrational way. I don't need to prove in detail that the squares in this case are not pairwise equal.