Praktische Ratschläge, bitte.

[Gelöscht] 2020.06.06 17:18

Frage: Wie kann ich die Ergebnisse richtig auswerten?

Der Fehler der einzelnen Module wird in Prozent angegeben. 0% ist das ideale Ergebnis.

________________ PARAMETER ________________	Mod 1	Mod 2	Mod 3	Modus 4	Modus 5	(vi) Modus 6	(vi) Modus 7	(vi) Modus 8	(vi) Mod 9	(vi) Mod 10	(vi) Mod 11	(vi) Mod 12	(viii) mod 13	(vi) 14	Modus 15	Durchschnittlicher Fehler	Von den Versuchen
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

Ich möchte, dass der Fehler eines jeden Moduls minimal ist, aber ich möchte auch, dass die Streuung minimal ist.

Alexandr Andreev 2020.06.06 17:50 #1

Сергей Таболин:

Frage: Wie kann ich die Ergebnisse richtig auswerten?

Der Fehler der einzelnen Module wird in Prozent angegeben. 0% ist das ideale Ergebnis.

________________ PARAMETER ________________	Mod 1	Mod 2	Mod 3	Modus 4	Modus 5	(vi) Modus 6	(vi) Modus 7	(vi) Modus 8	(vi) Mod 9	(vi) Mod 10	(vi) Mod 11	(vi) Mod 12	(viii) mod 13	(vi) 14	Modus 15	Durchschnittlicher Fehler	Von den Versuchen
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

Ich möchte, dass der Fehler eines jeden Moduls minimal ist, aber ich möchte auch, dass die Streuung minimal ist.

Produkt der Logarithmen

ZS: Ich bin mir nicht ganz sicher, was erforderlich ist, aber der Logarithmus wird es ermöglichen, Fehler progressiv zu behandeln, er wird in Einzelfällen (einzelne Module) bessere Ergebnisse liefern. Und die Multiplikation ist ein Versuch, die Streuung zu verringern.

Hilfe bei der Codierung Wie Sie Ihre Produkte, FOREX - Trends, Prognosen

[Gelöscht] 2020.06.06 18:05 #2

Alexandr Andreev:

Produkt der Logarithmen

ZS: Ich verstehe nicht ganz, was genau verlangt wird, aber der Logarithmus wird es ermöglichen, Fehler progressiv zu behandeln, er wird in Einzelfällen (einzelne Module) bessere Ergebnisse liefern. Und die Multiplikation ist ein Versuch, die Ausbreitung zu verringern

Ich danke Ihnen. Und wie ist espraktisch?

Alexandr Andreev 2020.06.06 18:22 #3

Сергей Таболин:

Ich danke Ihnen. Und wie ist daspraktisch?

Wahrscheinlich nur das Produkt von

Option1 ) Übersetzen Sie jedes Modul in den Stil (1-x%) und multiplizieren Sie sie..... die Antwort wird ebenfalls von der Einheit subtrahiert.

x% ist der Zellenwert

Option2

Mit Logarithmen nehmen wir einfach den Wert einer Zelle und zählen den Logarithmus davon)))), je näher der Wert an der Null ist, um eine progressive Auswertung zu erhalten, d.h. mit einer Basiseinstellung ist 0,1 besser als 0,01 und auch 0,1 ist besser als 1. Es gibt nur einen Basisparameter für den Logarithmus, mit dem es sich lohnt, herumzuspielen.

Von der Theorie zur [WARNUNG GESCHLOSSEN!] Alle Fragen Maschinelles Lernen im Handel:

[Gelöscht] 2020.06.06 20:51 #4

Alexandr Andreev:

Vielleicht würde ein einfaches Produkt ausreichen.

Option1 ) Übersetzen Sie jedes Modul in den Stil (1-x%) und multiplizieren Sie sie..... Die Antwort wird ebenfalls von der Einheit abgezogen.

x% ist der Zellenwert

Option2

Mit Logarithmen nehmen wir einfach den Wert einer Zelle und zählen den Logarithmus davon)))), je näher der Wert an der Null ist, um eine progressive Auswertung zu erhalten, d.h. mit einer Basiseinstellung ist 0,1 besser als 0,01 und auch 0,1 ist besser als 1. Es gibt nur einen Basisparameter des Logarithmus, mit dem es sich lohnt, herumzuspielen.

Option 1

-3,43	-16,09	-14,82	-1,53	0,37	-16,72	-27,48	-4,70	-12,29	-4,70	-7,23	-5,33	0,37	-2,16	-5,96	10601305851,38
-4,06	-16,72	-11,66	-2,80	0,37	-18,62	-28,11	-3,43	-8,49	-4,06	-5,33	-5,33	-0,90	-0,90	-5,33	-6223799946,09
-3,43	-19,25	-15,46	-3,43	0,37	-16,72	-28,75	-5,33	-4,06	-7,23	-9,13	-4,06	0,37	-0,27	-3,43	1237520122,21

Was sagt mir das?

Option 2

-0,64640373	-1,23274206	-1,19920648	-0,40312052	0,200659451	-1,24846372	-1,45453998	-0,75587486	-1,12352498	-0,75587486	-0,91539984	-0,80140371	0,200659451	-0,49968708	-0,84260924
-0,70415052	-1,24846372	-1,10243371	-0,5797836	0,200659451	-1,292699	-1,46404221	-0,64640373	-0,97726621	-0,70415052	-0,80140371	-0,80140371	-0,2787536	-0,2787536	-0,80140371
-0,64640373	-1,30642503	-1,21642983	-0,64640373	0,200659451	-1,24846372	-1,47348697	-0,80140371	-0,70415052	-0,91539984	-1,00560945	-0,70415052	0,200659451	-0,10380372	-0,64640373

Dies ist der Logarithmus zur Basis 0,1

Was soll ich damit machen?

Ich habe andere Funktionen ausprobiert. Nur wie kann ich sie auch verstehen? ....

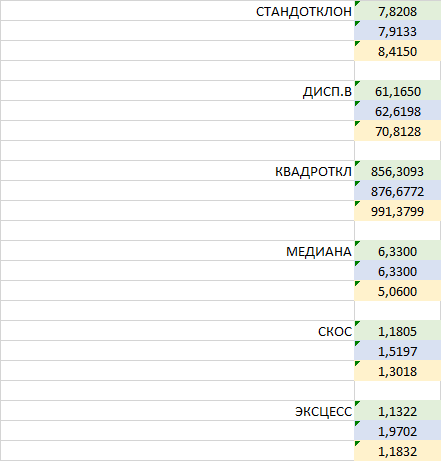
STANDOTCLONE	7,8208
	7,9133
	8,4150

DISP.B	61,1650
	62,6198
	70,8128

QUADROTKL	856,3093
	876,6772
	991,3799

MEDIANA	6,3300
	6,3300
	5,0600

SCOS	1,1805
	1,5197
	1,3018

EXZESS	1,1322
	1,9702
	1,1832

Practical advice, please. Circular Buffer Issue MQL5 PREDICT time period

Dmitry Fedoseev 2020.06.06 20:58 #5

Ermitteln Sie das Maximum in jeder Zeile und wählen Sie dann die Zeile mit dem kleinsten Maximum aus. Verzeihen Sie das Wortspiel))

[Gelöscht] 2020.06.06 21:12 #6

Dmitry Fedoseev:
Finde das Maximum in jeder Zeile und wähle dann die Zeile mit dem kleinsten Maximum. Verzeihen Sie das Wortspiel))

Maximalwert in Zeile 3, Minimalwert in Zeile 1. И? )))

Dmitry Fedoseev 2020.06.06 21:18 #7

Сергей Таболин:

Maximalwert in Zeile 3, Minimalwert in Zeile 1. И? )))

Wählen Sie die erste Zeile.

Alexandr Andreev 2020.06.06 23:15 #8

Сергей Таболин:

Option 1

-3,43	-16,09	-14,82	-1,53	0,37	-16,72	-27,48	-4,70	-12,29	-4,70	-7,23	-5,33	0,37	-2,16	-5,96	10601305851,38
-4,06	-16,72	-11,66	-2,80	0,37	-18,62	-28,11	-3,43	-8,49	-4,06	-5,33	-5,33	-0,90	-0,90	-5,33	-6223799946,09
-3,43	-19,25	-15,46	-3,43	0,37	-16,72	-28,75	-5,33	-4,06	-7,23	-9,13	-4,06	0,37	-0,27	-3,43	1237520122,21

Was sagt mir das?

Option 2

-0,64640373	-1,23274206	-1,19920648	-0,40312052	0,200659451	-1,24846372	-1,45453998	-0,75587486	-1,12352498	-0,75587486	-0,91539984	-0,80140371	0,200659451	-0,49968708	-0,84260924
-0,70415052	-1,24846372	-1,10243371	-0,5797836	0,200659451	-1,292699	-1,46404221	-0,64640373	-0,97726621	-0,70415052	-0,80140371	-0,80140371	-0,2787536	-0,2787536	-0,80140371
-0,64640373	-1,30642503	-1,21642983	-0,64640373	0,200659451	-1,24846372	-1,47348697	-0,80140371	-0,70415052	-0,91539984	-1,00560945	-0,70415052	0,200659451	-0,10380372	-0,64640373

Dies ist der Logarithmus zur Basis 0,1

Was soll ich damit machen?

Ich habe andere Funktionen ausprobiert. Aber wie kann ich sie auch verstehen?

"Der Fehler jedes Moduls wird in Prozent angegeben. 0% ist das ideale Ergebnis" Die Zahl 1 bedeutet 100% - x% oder 1-X*0,01

Alexandr Andreev 2020.06.06 23:19 #9

@Sergey Tabolin @Sergey Tabolin

															GESAMT
0,9557	0,8291	0,8418	0,9747	0,9937	0,8228	0,7152	0,943	0,8671	0,943	0,9177	0,9367	0,9937	0,9684	0,9304	0,77439
0,9494	0,8228	0,8734	0,962	0,9937	0,8038	0,7089	0,9557	0,9051	0,9494	0,9367	0,9367	0,981	0,981	0,9367	0,758606
0,9557	0,7975	0,8354	0,9557	0,9937	0,8228	0,7025	0,9367	0,9494	0,9177	0,8987	0,9494	0,9937	0,9873	0,9557	0,771806

die zweite Zeile ist die beste, und die erste und die dritte sind sehr ähnlich

die von der Einheit abgezogene Gesamtsumme, d.h. je näher die Gesamtsumme an 0 liegt, desto besser sind die Ergebnisse..... mit anderen Worten, die bisherigen Ergebnisse sind nicht sehr gut, denn 0,75 ist Ihre 75, obwohl es davon abhängt, womit man sie vergleicht..... das schlechteste Ergebnis wäre 1 (100%) das beste Ergebnis 0

Sie müssen verstehen, dass ein Ergebnis von 90 zehnmal besser ist als ein Ergebnis von 99.... eine Punktzahl von 99 ist zehnmal besser als eine Punktzahl von 99,9... 100 ist in der Tat nur möglich, wenn alle Module eine Fehlerpunktzahl von 100 haben... d.h. ein Wert von 0,1 ist zehnmal schlechter als ein Wert von 0,01. Gleichzeitig ist ein Wert von 10 zehnmal schlechter als ein Wert von 1.

mit dem Logarithmus über think..... sollte die Antwort ausschließlich positive Werte sein... normalerweise ein Logarithmus von 1,1... im Bereich von 1 bis 2, nicht 0 bis 1.... wenn sie die Zahl erhöhen wollen und ab 2, wenn sie sie schrittweise verringern wollen

Die quadratische Abweichungsmethode kommt definitiv nicht in Frage. Das gilt auch für alle anderen, die Abweichungen zählen. Denn idealerweise würde man die quadratische Abweichung von einer linearen Regression verwenden, um die Varianz zu verstehen. Aber dann erhalten wir eine Schätzung dieser Abweichungen ohne einen Durchschnitt der Zahlen selbst.....

Practical advice, please. [Archiv!] Reine Mathematik, Physik, Portfolio: PriceChannelExpert und andere

Roman 2020.06.07 03:48 #10

Сергей Таболин:

Frage: Wie kann ich die Ergebnisse richtig auswerten?

Der Fehler der einzelnen Module wird in Prozent angegeben. 0% ist das ideale Ergebnis.

________________ PARAMETER ________________	Mod 1	Mod 2	Mod 3	Modus 4	Modus 5	(vi) Modus 6	(vi) Modus 7	(vi) Modus 8	(vi) Mod 9	(vi) Mod 10	(vi) Mod 11	(vi) Mod 12	(viii) mod 13	(vi) 14	Modus 15	Durchschnittlicher Fehler	Von den Versuchen
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

Ich möchte, dass der Fehler der einzelnen Module minimal ist, aber ich möchte auch, dass die Streuung minimal ist.

Es ist wahrscheinlich besser, die Summe der Quadrate für die Modulfehler zu ermitteln und die Wurzel zu extrahieren.
Auf diese Weise erhalten wir eine Schätzung des gesamten Modulfehlers.
Je näher dieser Wert bei Null liegt, desto besser.
Es geht also folgendermaßen.

//+------------------------------------------------------------------+
//|                                                EstimateError.mq5 |
//|                        Copyright 2020, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2020, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"


double ModN[15][3] = {{4.43, 5.06, 4.43},
                      {17.09, 17.72, 20.25},
                      {15.82, 12.66, 16.46},
                      {2.53, 3.80, 4.43},
                      {0.63, 0.63, 0.63},
                      {17.72, 19.62, 17.72},
                      {28.48, 29.11, 29.75},
                      {5.70, 4.43, 6.33},
                      {13.29, 9.49, 5.06},
                      {5.70, 5.06, 8.23},
                      {8.23, 6.33, 10.13},
                      {6.33, 6.33, 5.06},
                      {0.63, 6.33, 0.63},
                      {3.16, 1.90, 1.27},
                      {6.96, 6.33, 4.43}};

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
{
   double ModX[];
   ArrayResize(ModX, 3);
   ZeroMemory(ModX);   
   
   int    num = 1;
   double est = 0.0;
   
   for(int i=0; i<15; i++)
   {
      for(int j=0; j<3; j++)
      {
         ModX[j] = ModN[i][j];         
      }
         
      est = EstimateError(ModX);  
      
      PrintFormat("Mod"+(string)num+" EstimateError: %.3f", est); 
      num++;
   }         
}// End OnStart

//+------------------------------------------------------------------+
double EstimateError(double & arr[])
{
   int size = ArraySize(arr);
   if(size == 0 || size < 3) 
      return(0.0);
   
   //double avg       = ArrayMean(arr); 
   double max       = ArrayMax(arr);   
   double min       = ArrayMin(arr); 
   double sum_sqr_e = 0.0;
   double est_e     = 0.0;      
   
   
   for(int i=0; i<size; i++)   
      sum_sqr_e += MathPow(arr[i] - (max-min)/* или avg*/, 2.0) / (size - 2.0);
      
   est_e = MathSqrt(sum_sqr_e);   

   return(est_e);
}

//+-------------------------------------------------------------------
//Возвращает максимальное значение элементов массива
double ArrayMax(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);          
   
   double max = arrIn[0];
   for(uint i=1; i<size; i++)
      if(arrIn[i] > max) 
         max = arrIn[i];

   return(max);
}

//--------------------------------------------------------------------
//Возвращает минимальное значение элементов массива
double ArrayMin(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);   
   
   double min = arrIn[0];  
   for(uint i=1; i<size; i++)
      if(arrIn[i] < min) 
         min = arrIn[i];

   return(min);
}

//--------------------------------------------------------------------
//Возвращает средне арефметическое значение элементов массива
double ArrayMean(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);         

   double sum = 0.0;       
   for(uint i=0; i<size; i++) 
      sum += arrIn[i];     
   
   return(sum/size);
}

//--------------------------------------------------------------------

2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod1 EstimateError: 6.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod2 EstimateError: 26.422
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod3 EstimateError: 19.577
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod4 EstimateError: 3.226
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod5 EstimateError: 1.091
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod6 EstimateError: 28.540
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod7 EstimateError: 48.234
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod8 EstimateError: 6.361
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod9 EstimateError: 6.102
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod10 EstimateError: 5.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod11 EstimateError: 8.130
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod12 EstimateError: 8.098
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod13 EstimateError: 7.198
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod14 EstimateError: 1.413
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod15 EstimateError: 6.138

Die Schätzung zeigt, dass Mod5 den geringsten Fehler aufweist.

Handelswahrscheinlichkeit Maschinelles Lernen im Handel: Absolute Kurse

1 2 3 4 5 6 7

Neuer Kommentar