Diskussion zum Artikel "Tiefe neuronale Netzwerke (Teil V). Bayes'sche Optimierung von DNN-Hyperparametern"
Ich habe mit BayesianOptimisation experimentiert.
Sie hatten den größten Satz von 9 optimierbaren Parametern. Und Sie sagten, dass die Berechnung sehr lange dauert.
Ich habe versucht, einen Satz von 20 Parametern mit 10 ersten Zufallsmengen zu optimieren. Ich habe 1,5 Stunden gebraucht, um die Kombinationen in BayesianOptimisation zu berechnen, ohne die Berechnungszeit für den NS selbst zu berücksichtigen (ich habe den NS durch eine einfache mathematische Formel für das Experiment ersetzt).
Und wenn Sie 50 oder 100 Parameter optimieren wollen, dauert es wahrscheinlich 24 Stunden, um 1 Satz zu berechnen. Ich denke, es wäre schneller, Dutzende von Zufallskombinationen zu erzeugen und sie in NS zu berechnen und dann die besten nach Genauigkeit auszuwählen.
In der Paketdiskussion wird über dieses Problem gesprochen. Vor einem Jahr schrieb der Autor, dass er, wenn er ein schnelleres Paket für die Berechnungen findet, es verwenden wird, aber im Moment - so wie es ist. Es gibt ein paar Links zu anderen Paketen mit Bayes'scher Optimierung, aber es ist nicht klar, wie man sie für ein ähnliches Problem anwenden kann, in den Beispielen werden andere Probleme gelöst.
bigGp - findet den SN2011fe-Datensatz für das Beispiel nicht (offenbar wurde er aus dem Internet heruntergeladen, und die Seite ist nicht verfügbar). Ich konnte das Beispiel nicht ausprobieren. Und laut Beschreibung sind einige zusätzliche Matrizen erforderlich.
laGP - einige verwirrende Formeln in der Fitnessfunktion, und macht Hunderte von Aufrufen, und Hunderte von NS-Berechnungen sind in Bezug auf die Zeit inakzeptabel.
kofnGA - kann nur X beste aus N suchen. Zum Beispiel 10 von 100. D.h. er optimiert nicht eine Menge von allen 100.
Genetische Algorithmen sind auch nicht geeignet, weil sie ebenfalls Hunderte von Aufrufen der Fitnessfunktion (NS-Berechnungen) erzeugen.
Im Allgemeinen gibt es kein Analogon, und die Bayes'sche Optimierung selbst ist zu lang.
Ich habe mit BayesianOptimisation experimentiert.
Sie hatten den größten Satz von 9 optimierbaren Parametern. Und Sie sagten, dass die Berechnung sehr lange dauert
Ich habe versucht, einen Satz von 20 Parametern mit 10 ersten Zufallsmengen zu optimieren. Ich habe 1,5 Stunden gebraucht, um die Kombinationen selbst in BayesianOptimisation zu berechnen, ohne die Zeit für die Berechnung der NS selbst zu berücksichtigen (ich habe die NS durch eine einfache mathematische Formel für das Experiment ersetzt).
Und wenn Sie 50 oder 100 Parameter optimieren wollen, dauert es wahrscheinlich 24 Stunden, um 1 Satz zu berechnen. Ich denke, es wäre schneller, Dutzende von Zufallskombinationen zu erzeugen und sie in NS zu berechnen und dann die besten nach Genauigkeit auszuwählen.
In der Paketdiskussion wird über dieses Problem gesprochen. Vor einem Jahr schrieb der Autor, dass er, wenn er ein schnelleres Paket für die Berechnungen findet, es verwenden wird, aber im Moment - so wie es ist. Es wurden ein paar Links zu anderen Paketen mit Bayes'scher Optimierung angegeben, aber es ist nicht klar, wie man sie für ein ähnliches Problem anwenden kann, in den Beispielen werden andere Probleme gelöst.
bigGp - findet den SN2011fe-Datensatz für das Beispiel nicht (anscheinend wurde er aus dem Internet heruntergeladen, und die Seite ist nicht verfügbar). Ich konnte das Beispiel nicht ausprobieren. Und laut Beschreibung sind einige zusätzliche Matrizen erforderlich.
laGP - einige verwirrende Formeln in der Fitnessfunktion, und macht Hunderte von Aufrufen, und Hunderte von NS-Berechnungen sind in Bezug auf die Zeit inakzeptabel.
kofnGA - kann nur X beste aus N suchen. Zum Beispiel 10 von 100. D.h. er optimiert nicht eine Menge von allen 100.
Genetische Algorithmen sind ebenfalls nicht geeignet, da sie ebenfalls Hunderte von Aufrufen der Fitnessfunktion (NS-Berechnungen) erzeugen.
Im Allgemeinen gibt es kein Analogon, und die Bayes'sche Optimierung selbst ist zu lang.
Es gibt ein solches Problem. Es hängt mit der Tatsache zusammen, dass das Paket in reinem R geschrieben ist. Aber die Vorteile der Verwendung überwiegen für mich persönlich die Zeitkosten. Es gibt ein Paket hyperopt (Python)/ Ich hatte noch nicht die Gelegenheit, es auszuprobieren, und es ist alt.
Aber ich denke, jemand wird das Paket noch in C++ umschreiben. Natürlich kann man es auch selbst machen, indem man einen Teil der Berechnungen auf die GPU überträgt, aber das wird sehr viel Zeit in Anspruch nehmen. Nur wenn ich wirklich verzweifelt bin.
Im Moment werde ich das benutzen, was ich habe.
Viel Glück!
Ich habe auch mit Beispielen aus dem GPfit-Paket selbst experimentiert.
Hier ist ein Beispiel für die Optimierung eines Parameters, der eine Kurve mit 2 Scheitelpunkten beschreibt (das GPfit-Paket f-ya hat mehr Scheitelpunkte, ich habe 2 gelassen):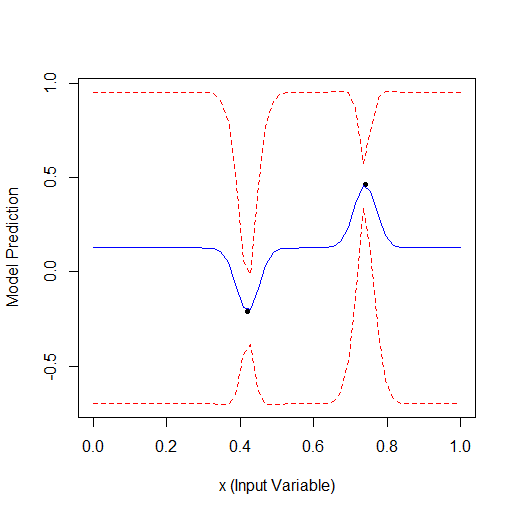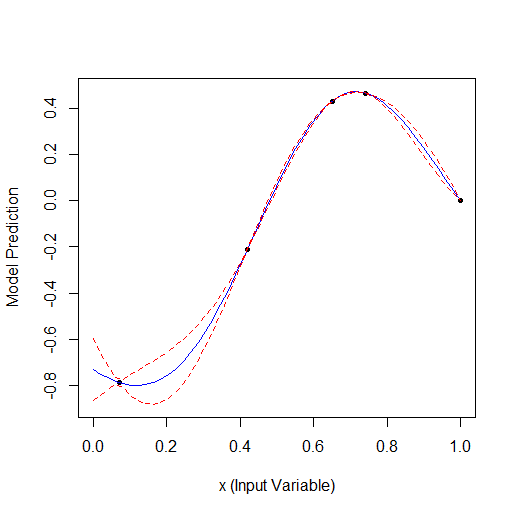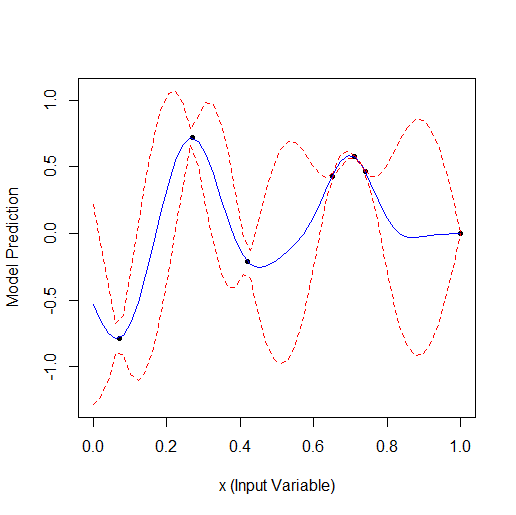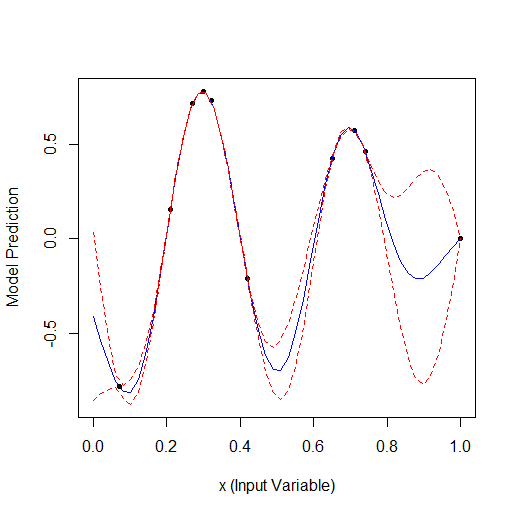
Nehmen Sie 2 zufällige Punkte und optimieren Sie dann. Sie können sehen, dass zuerst der kleine Scheitelpunkt und dann der größere Scheitelpunkt gefunden wird. Insgesamt 9 Berechnungen - 2 zufällige und + 7 bei der Optimierung.
Ein weiteres Beispiel in 2D - Optimierung von 2 Parametern. Das ursprüngliche f-y sieht wie folgt aus: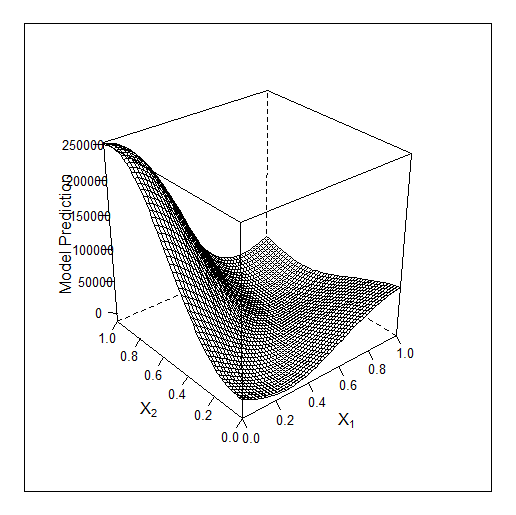
Optimierung auf 19 Punkte:

Insgesamt 2 zufällige Punkte + 17 vom Optimierer gefundene Punkte.
Beim Vergleich dieser beiden Beispiele können wir sehen, dass sich die Anzahl der Iterationen, die erforderlich sind, um das Maximum zu finden, verdoppelt, wenn 1 Parameter hinzugefügt wird. Für 1 Parameter wurde das Maximum für 9 berechnete Punkte gefunden, für 2 Parameter für 19.
D.h. wenn Sie 10 Parameter optimieren, benötigen Sie 9 * 2^10 = 9000 Berechnungen.
Obwohl der Algorithmus bei 14 Punkten fast das Maximum gefunden hat, ist dies etwa die 1,5-fache Anzahl von Berechnungen. 9 * 1,5:10 = 518 Berechnungen. Auch das ist viel, für eine akzeptable Rechenzeit.
Die in dem Artikel erzielten Ergebnisse für 20 - 30 Punkte sind möglicherweise weit vom tatsächlichen Maximum entfernt.
Ich denke, dass genetische Algorithmen selbst bei diesen einfachen Beispielen viel mehr Punkte zur Berechnung benötigen. Es gibt also wahrscheinlich keine bessere Option.
Ich habe auch mit Beispielen aus dem GPfit-Paket selbst experimentiert.
Hier ist ein Beispiel für die Optimierung eines Parameters, der eine Kurve mit 2 Scheitelpunkten beschreibt (das GPfit f-ya hat mehr Scheitelpunkte, ich habe 2 belassen):
Nehmen Sie 2 zufällige Punkte und optimieren Sie dann. Sie können sehen, dass zuerst der kleine Scheitelpunkt und dann der größere Scheitelpunkt gefunden wird. Insgesamt 9 Berechnungen - 2 zufällige und + 7 bei der Optimierung.
Ein weiteres Beispiel in 2D - Optimierung von 2 Parametern. Das ursprüngliche f-ya sieht wie folgt aus:
Optimieren Sie bis zu 19 Punkte:
Insgesamt 2 zufällige Punkte + 17 vom Optimierer gefundene Punkte.
Vergleicht man diese beiden Beispiele, so sieht man, dass sich die Anzahl der Iterationen, die benötigt werden, um das Maximum zu finden, verdoppelt, wenn 1 Parameter hinzugefügt wird. Für 1 Parameter wurde das Maximum für 9 berechnete Punkte gefunden, für 2 Parameter für 19.
D.h. wenn Sie 10 Parameter optimieren, benötigen Sie 9 * 2^10 = 9000 Berechnungen.
Obwohl der Algorithmus bei 14 Punkten fast das Maximum gefunden hat, ist dies etwa die 1,5-fache Anzahl von Berechnungen. 9 * 1,5:10 = 518 Berechnungen. Auch das ist viel, für eine akzeptable Rechenzeit.
1. Die in dem Artikel erzielten Ergebnisse für 20 - 30 Punkte können weit vom tatsächlichen Maximum entfernt sein.
Ich denke, dass genetische Algorithmen selbst bei diesen einfachen Beispielen viel mehr Punkte berechnen müssen. Es gibt also wohl doch keine bessere Option.
Bravo!
Das ist klar.
Es gibt eine Reihe von Vorträgen auf YouTube, die erklären, wie die Bayes'sche Optimierung funktioniert. Wenn Sie sie noch nicht gesehen haben, empfehle ich Ihnen, sie anzusehen. Es ist sehr informativ.
Wie haben Sie die Animation eingefügt?
Ich versuche, wo immer möglich, Bayes'sche Methoden zu verwenden. Die Ergebnisse sind sehr gut.
1. Ich mache eine sequentielle Optimierung. Erste - Initialisierung von 10 zufälligen Punkten, Berechnung von 10-20 Punkten, nächste - Initialisierung der 10 besten Ergebnisse der vorherigen Optimierung, Berechnung von 10-20 Punkten. In der Regel verbessern sich die Ergebnisse nach der zweiten Iteration nicht mehr nennenswert.
Viel Glück
Eine Reihe von Vorträgen, die erklären, wie die Bayes'sche Optimierung funktioniert, sind auf YouTube zu finden. Wenn Sie sie noch nicht gesehen haben, empfehle ich Ihnen, sie anzusehen. Sie sind sehr informativ.
Ich habe mir den Code und das Ergebnis in Form von Bildern angesehen (und es Ihnen gezeigt). Das Wichtigste ist der Gaußsche Prozess von GPfit. Und die Optimierung ist das Üblichste - verwenden Sie einfach den Optimierer aus der Standard-R-Lieferung und suchen Sie das Maximum auf der Kurve/Form, die GPfit um 2, 3 usw. Punkte erhöht hat. Was dabei herausgekommen ist, können Sie in den animierten Bildern oben sehen. Der Optimierer versucht nur, die 100 besten Zufallspunkte herauszufinden.
Vielleicht werde ich mir in Zukunft Vorlesungen ansehen, wenn ich Zeit habe, aber im Moment werde ich GPfit nur als Blackbox verwenden.
Wie haben Sie die Animation eingefügt?
Ich habe das Ergebnis einfach Schritt für Schritt mit GPfit::plot.GP(GP, surf_check = TRUE) dargestellt, in Photoshop eingefügt und dort als animiertes GIF gespeichert.
Nachfolgend - Initialisierung der 10 besten Ergebnisse aus der vorherigen Optimierung, Berechnungen von 10-20 Punkten.
Meinen Experimenten zufolge ist es besser, alle bekannten Punkte für künftige Berechnungen beizubehalten, denn wenn die unteren Punkte entfernt werden, könnte GPfit denken, dass es interessante Punkte gibt, und wird sie berechnen wollen, d.h. es wird wiederholte Durchläufe der NS-Berechnung geben. Und mit diesen unteren Punkten wird GPfit wissen, dass es in diesen unteren Regionen nichts zu suchen gibt.
Wenn sich die Ergebnisse jedoch nicht wesentlich verbessern, bedeutet dies, dass es ein umfangreiches Plateau mit kleinen Schwankungen gibt.
Wie installiert und startet man ?
).

- 2016.04.26
- Vladimir Perervenko
- www.mql5.com
Vorwärtstests der Modelle mit optimalen Parametern
Lassen Sie uns prüfen, wie lange die optimalen Parameter des DNN Ergebnisse mit akzeptabler Qualität für die Tests der "zukünftigen" Kurswerte liefern werden. Der Test wird in der nach den vorangegangenen Optimierungen und Tests verbleibenden Umgebung wie folgt durchgeführt.
Verwenden Sie ein gleitendes Fenster von 1350 Balken, train = 1000, test = 350 (für die Validierung - die ersten 250 Stichproben, für den Test - die letzten 100 Stichproben) mit Schritt 100, um die Daten nach den ersten (4000 + 100) Balken, die für das Pretraining verwendet wurden, durchzugehen. Machen Sie 10 Schritte "vorwärts". Bei jedem Schritt werden zwei Modelle trainiert und getestet:
- erstens - unter Verwendung des vortrainierten DNN, d.h. bei jedem Schritt wird eine Feinabstimmung für einen neuen Bereich durchgeführt;
- zweitens - zusätzliches Trainieren des DNN.opt, das nach der Optimierung in der Feinabstimmungsphase erhalten wurde, für einen neuen Bereich.
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
Der erste Teil des Vorwärtstests wird mit dem vortrainierten DNN und den optimalen Hyperparametern durchgeführt, die aus der Trainingsvariante SRBM + upperLayer + BP gewonnen wurden.
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
Zweiter Teil des Vorwärtstests unter Verwendung der während der Optimierung erhaltenen Dnn.opt:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
Vergleichen Sie die Testergebnisse und stellen Sie sie in einer Tabelle zusammen:
env$Score3_dnn env$Score3_dnnOpt
| iter | Ergebnis3_dnn | Ergebnis3_dnnOpt |
|---|---|---|
| Genauigkeit Präzision Rückruf F1 | Genauigkeit Präzision Rückruf F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 | -1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 | -1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 | -1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 | -1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 | -1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 | -1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 | -1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 | -1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 | -1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
Die Tabelle zeigt, dass die ersten beiden Schritte zu guten Ergebnissen führen. Die Qualität ist bei beiden Varianten in den ersten beiden Schritten gleich, danach sinkt sie. Daher kann davon ausgegangen werden, dass das DNN nach der Optimierung und dem Testen die Qualität der Klassifizierung auf dem Niveau des Testsatzes bei mindestens 200-250 folgenden Takten halten wird.
Es gibt noch viele andere Kombinationen für das zusätzliche Training von Modellen auf Vorwärtstests, die im vorigenArtikel erwähnt wurden, und zahlreiche einstellbare Hyperparameter.
Hallo, wie lautet die Frage?
Hallo Vladimir,
ich verstehe nicht ganz, warum Ihr NS auf Trainingsdaten trainiert wird und seine Auswertung auf Testdaten erfolgt (wenn ich mich nicht irre, verwenden Sie es als Validierung).
Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3)
Würden Sie in diesem Fall nicht eine Anpassung an das Testdiagramm erhalten, d. h. Sie würden das Modell auswählen, das auf dem Testdiagramm am besten funktioniert?
Wir sollten auch bedenken, dass die Testkurve ziemlich klein ist und es möglich ist, eine der zeitlichen Regelmäßigkeiten anzupassen, was sehr schnell aufhören kann zu funktionieren.
Vielleicht ist es besser, auf der Trainingskurve zu schätzen, oder auf der Summe der Kurven, oder wie in Darch (mit vorgelegten Validierungsdaten) auf Err = (ErrLeran * 0,37 + ErrValid * 0,63) - diese Koeffizienten sind Standardwerte, aber sie können geändert werden.
Es gibt viele Optionen, und es ist nicht klar, welche davon die beste ist. Ihre Argumente für den Testplot sind interessant.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Tiefe neuronale Netzwerke (Teil V). Bayes'sche Optimierung von DNN-Hyperparametern :
Der Artikel beschäftigt sich mit der Möglichkeit, die Bayes'sche Optimierung auf Hyperparameter von tiefen neuronalen Netzen anzuwenden, die durch verschiedene Trainingsvarianten gewonnen werden. Die Klassifikationsqualität eines DNN mit den optimalen Hyperparametern in verschiedenen Trainingsvarianten wird verglichen. Die Tiefe der Effektivität der optimalen DNN-Hyperparameter wurde in Vorwärtstests überprüft. Die möglichen Richtungen zur Verbesserung der Klassifizierungsqualität wurden festgelegt.
Das Ergebnis ist gut. Zeichnen wir eine Grafik des Trainingsablaufes:
plot(env$Res1$Dnn.opt, type = "class")Abb. 2. Trainingsablauf von DNN mit der Variante SRBM + RP
Wie aus der Abbildung ersichtlich, ist der Fehler auf dem Validierungssatz geringer als der Fehler auf dem Trainingssatz. Das bedeutet, dass das Modell nicht überdimensioniert ist und eine gute Verallgemeinerungsfähigkeit besitzt. Die rote senkrechte Linie zeigt die Ergebnisse des Modells an, das als das beste gilt und nach dem Training als Ergebnis zurückgegeben wird.
Für die anderen drei Trainingsvarianten werden nur die Ergebnisse von Berechnungen und Verlaufsgrafik ohne weitere Angaben zur Verfügung gestellt. Alles wird ähnlich berechnet.
Autor: Vladimir Perervenko