你好,Ndawana
首先感谢你撰写这篇文章并简化人工智能的神话:)我正试图在我的代码中使用由此生成的信号,但需要做一些修改。
能否解释一下您在代码中使用矢量而不是简单数组的原因?
你好,Anil,首先我想说的是,如果我们使用数组而不是矢量,不会有任何问题,所以我们可以使用简单数组来代替。
,我对矢量的偏好来自于只有矢量才能使用的特殊函数,除了这些特殊函数外,矢量还允许我们同时对所有元素进行计算。下面是一个简单的例子。
,我对矢量的偏好来自于只有矢量才能使用的特殊函数,除了这些特殊函数外,矢量还允许我们同时对所有元素进行计算。下面是一个简单的例子。
//+------------------------------------------------------------------+ //|Anil.mq5 | | //|Gamuchirai Zororo Ndawana | | //|https://www.mql5.com/en/gamuchiraindawa| |. //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| 脚本程序启动功能| //+------------------------------------------------------------------+ void OnStart() { //--- 我在数组方面遇到的问题是 double anil_array[3]; ArrayFill(anil_array,0,3,0); ArrayPrint(anil_array); //--- 我们必须遍历所有元素以进行计算 for(int i = 0; i < 3; i++) { anil_array[i] += 1; } ArrayPrint(anil_array); //--- 对向量进行同样的操作 vector anil_vector = vector::Zeros(3); /Simillar 到一个充满零的数组 Print(anil_vector); //-- 向量允许我们同时对所有元素进行计算 anil_vector = anil_vector + 1; Print(anil_vector); } //+------------------------------------------------------------------+
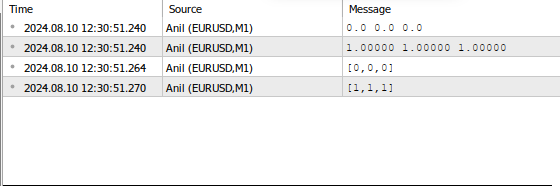 .
.
因此,试想一下,如果将来我们想到了一种可能有用的计算方法,那么由于我们使用的是矢量,修改代码库就会容易得多。
新文章 重塑经典策略(第二部分):布林带突破已发布:
本文探讨了一种将线性判别分析(LDA)与布林带相结合的交易策略,利用对市场区域的分类预测来生成战略性入场信号。
“人工智能”(AI)这个词可能是历史上最具误导性的命名惯例之一。读完本文后,你可能会同意AI是一个误称。作为作者,我对“智能”这个词有疑问。人工智能模型并非以人类意义上的智能存在。相反,它们是优化算法的智能应用。
人工智能模型的主要目标是在一个系统内最小化误差或最大化回报。然而,这些模型得出的解决方案并不总是实用的。例如,一个旨在最小化交易账户损失的人工智能系统可能会得出结论:不进行任何交易是最好的解决方案,因为这样可以保证没有损失。尽管从数学方面来看满足了问题本身,但这种解决方案对交易来说是不切实际的。
作为智能的人工智能实践者,我们必须用精心设计的约束条件来引导我们的模型。在本文中,我们将使用布林带来指导我们的人工智能模型。我们将识别出价格可能处于的四个区域。请注意,在任何给定时间价格只能处于以下这四个区域中的一个。
我们将训练一个模型,用以理解价格在这四个区域之间的转换,并预测价格将移动到的下一个区域。每当价格从一个区域转移到另一个区域时,就会生成交易信号。例如,如果我们的模型预测价格将从区域2移动到区域1,我们将此解释为向上移动,并发起买入订单。我们的模型和EA将完全用原生MQL5实现。
布林带可以在多种交易策略中使用,从趋势跟踪到识别转折点或反转点。从技术上讲,该指标由一条指数移动平均线(EMA)组成,通常用于平滑证券的收盘价。它由两条附加带包围:一条位于EMA的上方,另一条位于下方,每条通常设置为两个标准差。
作者:Gamuchirai Zororo Ndawana