你好!
你必须先建立一个参考框架。而这与价格和时间有关。
那么这都是几何学的问题。
你看,每个时间段都会有一个不同的相对论系统。Alexander Ivanov:
你好!
你好!
你必须先建立一个参考框架。而这与价格和时间有关。
那么这都是几何学的问题。
你看,每个时间段都会有一个不同的相对论系统。而这样的坐标系是如何构建的,你是如何想象的?
阿列克谢-维亚兹米 金。
你必须测量X轴上某一点的距离--这就是你的时间,我猜...
还是你必须用偏移量来实际测量?那么根据毕达哥拉斯定理--你知道两边和一个角......。
而且这也取决于距离是多少--以像素为单位?然后,你必须将所有东西转换为适当的坐标系,作为开始。如果你从逻辑上思考,红线应该与两条(黑色)线垂直--这将测量距离。我不关心这个值将被测量,最重要的是,当你改变刻度时,这个值不会改变。
我甚至试图这样做:取线交叉的值,并计算它之间的条数......。这种方法不适合用于改变规模!。
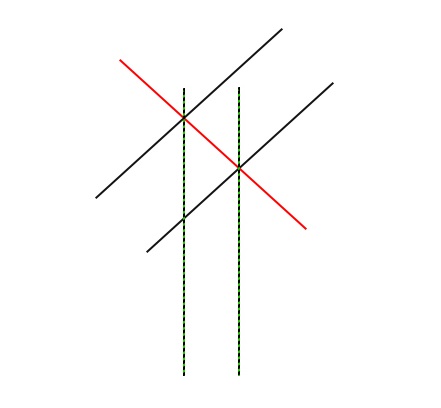
伊霍尔-赫拉斯科。
为了使刻度不受影响,有必要使用一个固定的图表刻度。否则,它将始终受到影响。
为什么?比例是多少呢?
你最初甚至有什么?你如何划定界限?必须有一个功能,或者说什么?
这是最基本的,华生...
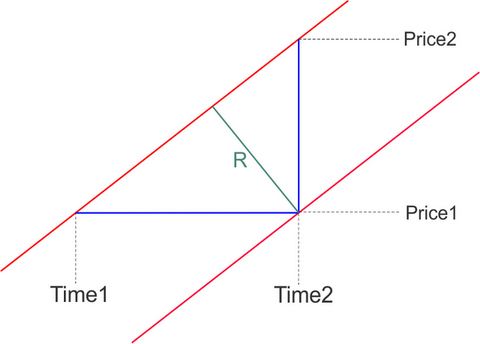
如果你想把二维系统Price X Time 投向平面Price X Price,你应该引入一个新的特性,更符合逻辑的是,它被称为价格变化的速度V。
而以每秒为单位来衡量是很方便的。
而V=你的线的角度的正切,在一个系统中与此成正比。
- 垂直方向的1个像素=1个_点
- 水平1个像素=1秒(1分钟条在你的屏幕上是60个像素的宽度)
那么两条平行线的距离可以用两种方法计算。
double V=(Price2-Price1)/(Time2-Time1); ulong DeltaTime = TimeLine2-TimeLine1; // double DeltaPrice = PriceLine2- PriceLine1; double R=DeltaTime*V/sqrt(1+V*V) ; // double R=V/(DeltaPrice*sqrt(1+V*V)) ; // где // точки (Price1,Time1) и (Price2,Time2) это две любые точки лежащие на одной из параллельных линий, Time измеряется в секундах // TimeLine1 и TimeLine2 - время первой и второй линии при фиксированной цене (пересечение с горизонтальной линией) // PriceLine1 и PriceLine2- цена первой и второй линии при фиксированном времени (пересечение с вертикальной линией) // DeltaPrice - расстояние между линиями в пунктах по вертикали // DeltaTime - расстояние между линиями в секундах по горизонтали // R - искомое кратчайшее расстояние между двумя параллельными линиями, скорость измерения цены которых равна V пунктов в секунду
很明显,这个垂直线在一个比例与上述系统不同的系统中不会看起来像一个垂直线。
Nikolai Semko:
这是最基本的,华生...
为了把二维的 "价格X时间"系统引入 "价格X价格"平面,有必要引入一个新的特性,更符合逻辑的是,它被称为价格变化的速度V。
而以每秒为单位来衡量是很方便的。
而V=你的线的角度的正切,在一个系统中与此成正比。
- 垂直方向的1个像素=1个_点
- 水平1个像素=1秒(1分钟条在你的屏幕上是60个像素的宽度)
那么两条平行线的距离可以用两种方法计算。
很明显,这个垂直线在一个比例不同于上述系统的系统中不会作为垂直线出现
我们可以简化这一点,因为有一种情况是Time1=TimeLine1,Time2=TimeLine2。
然后。
double V=(Price2-Price1)/(Time2-Time1); double R=(Price2-Price1)/sqrt(1+V*V) ;
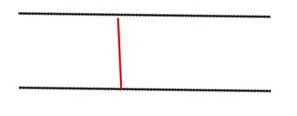
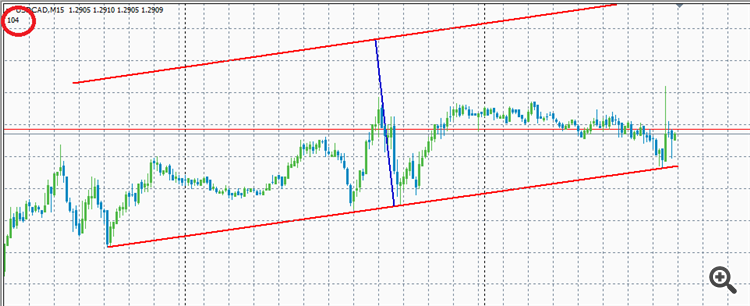
你能告诉我如何计算两条平行线之间的距离,包括图形的比例(使比例不受影响)?
下面是一个例子。
红线是两条平行线之间的距离 - 你如何计算?