Если оба процесса независимые, то оба они просто шум. Если ты складываешь или вычитаешь два шума, то получаешь просто третий шум. Т.е. результирующий процесс будет
y(i) = y(i-1) + e(i), где e(i) = b(i)+s(i) или e(i) = b(i)-s(i); + или - это не имеет значения.
Случайное блуждание чистой воды. Мелкие модификации, типа типа обрезания паникёров, серьёзно ничего не изменят. Только если твои процессы будут не независимые, то могут начаться чудеса.
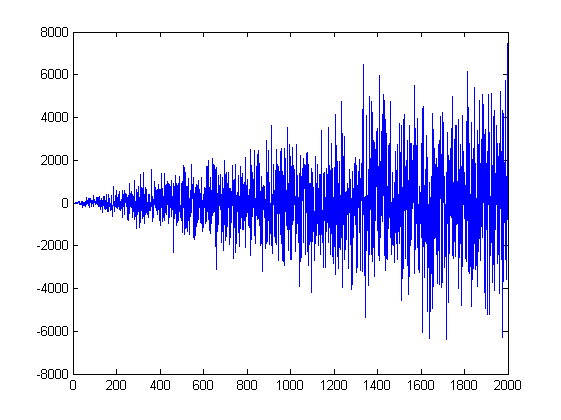
Не очень понял. Типа y(i) = y(i-1) + e(i) * i, где e(i) = b(i)+s(i)? Не удваивается, но возрастает. Удваивание слишком быстро вырастет. Даже простое умножение на i даёт вот такой рост приращений
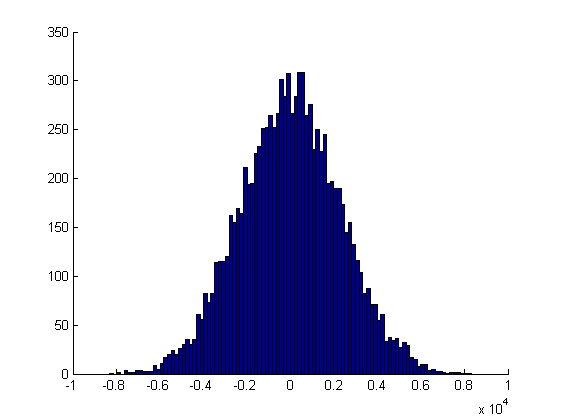
Однако, результирующий процесс y(i) остаётся нормальным, чего мы и ожидаем от случайного блуждания.
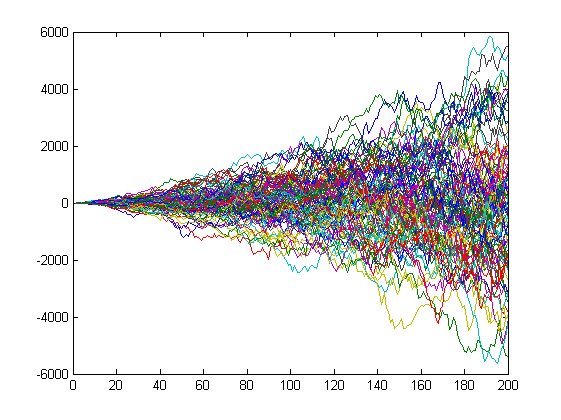
Хотя оно так может и не кажется на первый взгляд, но это только из-за изменения масштаба
avatara>>: На форуме часто в пылу дискуссии утверждается, что блуждание цены абсолютно случайно. Пускай не всегда. Но случайность и не... сложно якобы отличить. Теоремы арксинуса и двойного логарифма периодически обсуждаются или цитируются напрямую, либо только выводы. Мутно как то... У меня вопрос к теоретикам и практикам. Изучал ли кто "блуждание после соударения"? Постановка задачи следующая - есть два условных героя "БАЙ" и "СЕЛ". Пускай генерится некое приращение для каждого из них. В зависимости от героя назовём их "наступательным приращением" и "оборонительной силой". ...
avatara>>: супер! О удваивании следующее "прак...ое" наблюдение. Если на предыдущем шаге герой получил желаемое приращение (т.е |y(i)-y(i-1)|>= сила героя на i-том шаге, то его сгенерированную силу ( в том числе с минусом - сомнения) на i+1 шаге следует удвоить.
речь о моделировании случайных блужданий, что делается как правило стационарными распределниями - нормальным или дискретным. Можно наверное изголиться и смоделировать нестационарным. Сумма или разность нестационарных распределений будет так же нестационарна как правило, хотя есть исключения, которые лежат в основе коинтеграциии например
Если параметры распределений Б и С различны, то формулы для вычисления МО и дисперсии будут сложнее, но все равно будет такое же распредление
这是在C和B具有稳定分布的情况下。在这种情况下,是的,稳定分布的总和等于一个稳定分布。否则,不,具有不同分布的C和B的总和或差额将有一个地狱般的分布。
Если оба процесса независимые, то оба они просто шум. Если ты складываешь или вычитаешь два шума, то получаешь просто третий шум. Т.е. результирующий процесс будет
y(i) = y(i-1) + e(i), где e(i) = b(i)+s(i) или e(i) = b(i)-s(i); + или - это не имеет значения.
Случайное блуждание чистой воды. Мелкие модификации, типа типа обрезания паникёров, серьёзно ничего не изменят. Только если твои процессы будут не независимые, то могут начаться чудеса.
谢谢你的答复。
我能否再介绍一下对算法的修正?
如果英雄有了 "增量"--他的权力和疑虑会增加一倍。
那么这个随机的赞美学过程会是怎样的呢?
知道你所做的模型是类似的--你能看一下喇叭口/管道吗?这是在C和B具有稳定分布的情况下。在这种情况下,是的,稳定分布的总和等于一个稳定分布。否则,不,具有不同分布的C和B的总和或差额将有一个地狱般的分布。
我们正在讨论对随机漫步进行建模,这通常是用静止分布--正态或离散分布--来完成的。我们也许可以绕过它,把它作为非平稳的模型。非平稳分布的总和或差值通常也会是非平稳的,尽管有一些例外情况是协整的基础,例如:
Спасибо за ответ.
можно ввести еще одну поправку к алгоритму?
Если герой получил свое "приращение" - его силы и сомнения удваиваются.
Как тогда этот случайно праксиологический процесс будет смотреться?
Зная, что вы похожее моделировали - можно колокол/трубу глянуть?我不太明白。比如y(i) = y(i-1) + e(i) * i,其中e(i) = b(i)+s(i)?
不是翻倍,而是增加。倍增的速度会增长得太快。即使是简单地乘以i,也能得到这种增量的增长
然而,所产生的过程y(i)仍然是正常的,这就是我们对随机漫步的期望。
虽然乍看起来不是这样,但这只是由于规模的变化而造成的
Не очень понял. Типа y(i) = y(i-1) + e(i) * i, где e(i) = b(i)+s(i)?
Не удваивается, но возрастает. Удваивание слишком быстро вырастет. Даже простое умножение на i даёт вот такой рост приращений
Однако, результирующий процесс y(i) остаётся нормальным, чего мы и ожидаем от случайного блуждания.
Хотя оно так может и не кажется на первый взгляд, но это только из-за изменения масштаба
关于翻倍是以下 "实际 "的观察。
如果在上一步中,英雄得到了预期的增量(即|y(i)-y(i-1)|>=英雄在第i步中的力量,那么他在第i+1步中产生的力量(包括减去-疑)应该是双倍的。
这里的正弦波应该会放大,但我不确定。符号变异会妨碍我们;)
---
无礼的请求--将实施长度增加到500。 火灾
На форуме часто в пылу дискуссии утверждается, что блуждание цены абсолютно случайно.
Пускай не всегда. Но случайность и не... сложно якобы отличить.
Теоремы арксинуса и двойного логарифма периодически обсуждаются или цитируются напрямую, либо только выводы.
Мутно как то...
У меня вопрос к теоретикам и практикам.
Изучал ли кто "блуждание после соударения"?
Постановка задачи следующая - есть два условных героя "БАЙ" и "СЕЛ".
Пускай генерится некое приращение для каждого из них.
В зависимости от героя назовём их "наступательным приращением" и "оборонительной силой".
...
这里应该有一个脚注:如果增量是进攻性的,按照惯例,它必须优先于流动性的防御性增量。
要么在生成后的RPM中加入一个常数,要么设置一个移位的RPM范围。
那么我们将有一个进攻和一个防守,否则我们怎么知道谁在防守?
关于翻倍是以下 "实际 "的观察。
如果在上一步中,英雄得到了预期的增量(即|y(i)-y(i-1)|>=英雄在第i步中的力量,那么他在第i+1步中产生的力量(包括减去-双倍)应该是双倍的。
这里的正弦波应该会放大,但我不确定。符号变异会妨碍我们;)
你是否希望通过这样一个咖啡色的猜测来确定(或者说,来适应)市场分布?
супер!
О удваивании следующее "прак...ое" наблюдение.
Если на предыдущем шаге герой получил желаемое приращение (т.е |y(i)-y(i-1)|>= сила героя на i-том шаге, то его сгенерированную силу ( в том числе с минусом - сомнения) на i+1 шаге следует удвоить.
没有任何意义。这样的操作会改变增量的分布,它会长出大的尾巴,即使B和C是正态分布,但它不会改变所产生的过程的性质--它仍然是一个随机行走,并且是正态分布。只要第三时刻为零,即是对称的,随机行走就不关心增量的分布。
речь о моделировании случайных блужданий, что делается как правило стационарными распределниями - нормальным или дискретным. Можно наверное изголиться и смоделировать нестационарным. Сумма или разность нестационарных распределений будет так же нестационарна как правило, хотя есть исключения, которые лежат в основе коинтеграциии например
不要混淆温暖和柔软,即静止性与分布。他们没有任何关系。随机漫步有一个正态分布,但它不是静止的。均匀分布 是静止的,但两个均匀分布的总和不会是一个均匀分布。这是一个只属于稳定分布 的属性(在任何线性操作下保留分布的类型/形状)。
不要混淆温暖和柔软,即静止性与分布。他们没有任何关系。随机漫步有一个正态分布,但它不是静止的。均匀分布 是静止的,但两个均匀分布的总和不会是一个均匀分布。这是一个只属于稳定分布 的属性(在任何线性操作下保留分布的类型/形状)。
怎么会没有关系呢?正态分布是静止的,由NR分布的SB增量 是静止的,我原来说的是增量。
关于SB本身(作为增量的累积总和):不会有你在上一篇文章中描述的 "重尾"。因为在时间t 的SB本身也是正态分布,但其方差比一个增量(从原点出发的时间t)大t倍。是的,SB分布的方差随着时间的增加而增加。例如,超过3个希格玛的重尾,但对于SB来说,如果你计算某一特定时间的方差(你可以用分析方法来计算),它将与正常情况一样。
我同意SB过程本身不是静止的,它是一个具有单位根I(1)的非降级过程,即第一个差值(增量)是静止分布https://www.mql5.com/go?link=http://window.edu.ru/catalog/pdf2txt/141/28141/11363?p_page=55,但非静止分布不一定有重尾,在这种情况下将没有重尾。
你认为惠普是非稳态的吗?或者说,你不能对每个连续分布说它是否是静止的吗?:)