为什么正态分布不是正态? - 页 4 1234567891011...47 新评论 [删除] 2009.12.01 19:25 #31 太可怕了,人们这样乱说话,我不属于这里的失败者。 Петр 2009.12.01 19:31 #32 AlexEro >> : 恐怖。人们这样乱扔东西,我不属于这里。 我正在阅读,试图弄清楚他们要达成什么共识。 如果这是另一只羊第一次尝试给章鱼戴上一对流苏,那是一回事。如果是实用的东西,我就会参加。 Mykola Demko 2009.12.01 19:40 #33 Mathemat >> : 所以,中子来了,把所有东西都放在它的位置上。顺便说一下,Marketeer也在谈论峰度和不对称性。 相应的高斯曲线可以随心所欲地绘制,但这里最简单的是简单地计算样本方差并绘制参数为0和sigma的高斯曲线。这时你可以看到真正的直方图和这样的高斯曲线之间的区别。 顺便说一下,这个高斯近似值应该明显低于曲线中心(零点)的真实柱状图。 Urain,你把样品的s.c.o乘以多少? 另一方面,强厚尾分布的c.s.o.估计值取决于样本量,所以这里不是那么简单。 我根本没有碰过有效值,我只是拿了现成的图表,并将其按比例放大,以适应直方图的垂直方向。 直方图是Clos差异的分布(它有ME和RMS),这些ME和RMS被用来用上面的公式构建红线,但由于直方图的底部失去了线,而且构建比例y直方图的绝对x值很小,我们不得不将每条y线乘以一个乘数进行比较。 Yurixx 2009.12.01 19:47 #34 Urain писал(а)>> 对于参考函数,方差和MO取自一些报价(也是在那里计算的),并设置为相同的值,但唯一的操作是与基准的绝对值,这里我们必须把每项的系数加到顶点上,以结合起来。 据我所知,引用函数是一个HP函数。 如果是这样,你做的一切都对,除了一件事:你不能做任何域名。你想合并顶点的愿望与图形的实际位置没有关系。此外,域化违反了HP函数的规范化。你觉得概率>1的情况如何? 如果你去掉主宰,再做一次图片,这些地块在宽度上会或多或少地匹配。然而,直方图在中心和边缘会比较高,这表明有两个主要问题:更多的回报,同时,尾巴也很重。 如果你不介意的话,做一张这样的照片。 PS 我从以前的帖子中了解到你的问题。没有必要违反惠普的规范化。最好是为直方图找到合适的比例。它是从同样的配给中发现的。你必须把直方图中所有条形图的高度加起来,然后用这个值除以每个条形图。其结果是直方图也被归一化为1。 Mykola Demko 2009.12.01 19:48 #35 Svinozavr >> : 但我正在阅读--试图弄清楚他们会同意什么。 如果这又是第一次尝试给章鱼穿上一对褶皱,那是一回事。如果是实用的东西,我就会加入。 试图找出一系列报价的第一个差值中不在正态分布中的内容? Петр 2009.12.01 19:51 #36 Urain >> : 我试图找出,在报价序列的第一个差值中,有什么是正态分布中不存在的? 而这样做的目的是什么,目标是什么?确定 "异常 "的区域?同样,为什么? (到目前为止只有"?????")) Mykola Demko 2009.12.01 19:53 #37 Svinozavr >> : 而这样做的目的是什么,目标是什么?识别 "异常 "的区域?再一次--为什么? (到目前为止,一个"?????")) 比方说,要探究异常的规律表现在什么地方。 Mykola Demko 2009.12.01 19:58 #38 Yurixx >> : 我的理解是,参考函数是一个HP函数。 如果是这样,你做的一切都对,除了一件事:你不能做任何域名。你想合并顶点的愿望与图形的真实位置没有关系。此外,域化违反了HP函数的规范化。你觉得概率>1的情况如何? 如果你去掉主宰,再做一次图片,这些地块在宽度上会或多或少地匹配。然而,直方图在中心和边缘会比较高,这表明有两个主要问题:更多的回报,同时,尾巴也很重。 如果你不介意的话,做一张这样的照片。 PS 我从以前的帖子中了解到你的问题。没有必要违反惠普的规范化。最好是为直方图找到合适的比例。它是从同样的配给中发现的。你必须把直方图中所有条形图的高度加起来,然后用这个值除以每个条形图。其结果是,你的直方图也被归一了。 嗯,这不是什么大问题。你仍然需要把它规范化。 根本不存在配给问题。只有两者都调整为乘数=1.0/点;否则电感不会看到这么小的值。 Vladimir Gomonov 2009.12.01 20:14 #39 Neutron >> :.左下角是概率分布密度,右边是--同样的对数尺度。 如果分布是正态的,我们在这里会有一个抛物线,但它不是,因为有 "胖 "尾巴。原则上,我们应该在这里拟合一个最小二乘法的高斯,然后一切都会归位。我将不得不抛出一个最佳配合的公式... 谢尔盖,那么双对数呢? 我已经想了很久了......。 出于谦虚,我永远不能测试它 :) Neutron 2009.12.01 20:27 #40 MetaDriver >> : 谢尔盖,那么双对数呢? 我已经考虑了一段时间了... 我太谦虚了,不敢去看 :) 事实证明是这样。 可以看出,在零点附近,分布接近正态,然后以直线的形式进入渐近,在双对数尺度上,这表明 "尾巴 "分布的指数性质。换句话说,关于他们的 "沉重"。 1234567891011...47 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
恐怖。人们这样乱扔东西,我不属于这里。
我正在阅读,试图弄清楚他们要达成什么共识。
如果这是另一只羊第一次尝试给章鱼戴上一对流苏,那是一回事。如果是实用的东西,我就会参加。
所以,中子来了,把所有东西都放在它的位置上。顺便说一下,Marketeer也在谈论峰度和不对称性。
相应的高斯曲线可以随心所欲地绘制,但这里最简单的是简单地计算样本方差并绘制参数为0和sigma的高斯曲线。这时你可以看到真正的直方图和这样的高斯曲线之间的区别。
顺便说一下,这个高斯近似值应该明显低于曲线中心(零点)的真实柱状图。
Urain,你把样品的s.c.o乘以多少?
另一方面,强厚尾分布的c.s.o.估计值取决于样本量,所以这里不是那么简单。
我根本没有碰过有效值,我只是拿了现成的图表,并将其按比例放大,以适应直方图的垂直方向。
直方图是Clos差异的分布(它有ME和RMS),这些ME和RMS被用来用上面的公式构建红线,但由于直方图的底部失去了线,而且构建比例y直方图的绝对x值很小,我们不得不将每条y线乘以一个乘数进行比较。
对于参考函数,方差和MO取自一些报价(也是在那里计算的),并设置为相同的值,但唯一的操作是与基准的绝对值,这里我们必须把每项的系数加到顶点上,以结合起来。
据我所知,引用函数是一个HP函数。
如果是这样,你做的一切都对,除了一件事:你不能做任何域名。你想合并顶点的愿望与图形的实际位置没有关系。此外,域化违反了HP函数的规范化。你觉得概率>1的情况如何?
如果你去掉主宰,再做一次图片,这些地块在宽度上会或多或少地匹配。然而,直方图在中心和边缘会比较高,这表明有两个主要问题:更多的回报,同时,尾巴也很重。
如果你不介意的话,做一张这样的照片。
PS
我从以前的帖子中了解到你的问题。没有必要违反惠普的规范化。最好是为直方图找到合适的比例。它是从同样的配给中发现的。你必须把直方图中所有条形图的高度加起来,然后用这个值除以每个条形图。其结果是直方图也被归一化为1。
但我正在阅读--试图弄清楚他们会同意什么。
如果这又是第一次尝试给章鱼穿上一对褶皱,那是一回事。如果是实用的东西,我就会加入。
试图找出一系列报价的第一个差值中不在正态分布中的内容?
我试图找出,在报价序列的第一个差值中,有什么是正态分布中不存在的?
而这样做的目的是什么,目标是什么?确定 "异常 "的区域?同样,为什么?
(到目前为止只有"?????"))
而这样做的目的是什么,目标是什么?识别 "异常 "的区域?再一次--为什么?
(到目前为止,一个"?????"))
比方说,要探究异常的规律表现在什么地方。
我的理解是,参考函数是一个HP函数。
如果是这样,你做的一切都对,除了一件事:你不能做任何域名。你想合并顶点的愿望与图形的真实位置没有关系。此外,域化违反了HP函数的规范化。你觉得概率>1的情况如何?
如果你去掉主宰,再做一次图片,这些地块在宽度上会或多或少地匹配。然而,直方图在中心和边缘会比较高,这表明有两个主要问题:更多的回报,同时,尾巴也很重。
如果你不介意的话,做一张这样的照片。
PS
我从以前的帖子中了解到你的问题。没有必要违反惠普的规范化。最好是为直方图找到合适的比例。它是从同样的配给中发现的。你必须把直方图中所有条形图的高度加起来,然后用这个值除以每个条形图。其结果是,你的直方图也被归一了。
嗯,这不是什么大问题。你仍然需要把它规范化。
根本不存在配给问题。只有两者都调整为乘数=1.0/点;否则电感不会看到这么小的值。
.左下角是概率分布密度,右边是--同样的对数尺度。
如果分布是正态的,我们在这里会有一个抛物线,但它不是,因为有 "胖 "尾巴。原则上,我们应该在这里拟合一个最小二乘法的高斯,然后一切都会归位。我将不得不抛出一个最佳配合的公式...
谢尔盖,那么双对数呢? 我已经想了很久了......。
出于谦虚,我永远不能测试它 :)
谢尔盖,那么双对数呢? 我已经考虑了一段时间了...
我太谦虚了,不敢去看 :)
事实证明是这样。
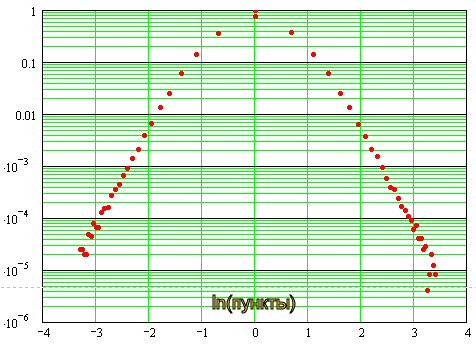
可以看出,在零点附近,分布接近正态,然后以直线的形式进入渐近,在双对数尺度上,这表明 "尾巴 "分布的指数性质。换句话说,关于他们的 "沉重"。