一般来说,悖论的话题是非常有趣的,并逐渐引向禅宗,教你虚心思考。
我已经被1-2+3-4+5系列洗脑了...=> 1/4
在不为人知的Terwer和Matstat中,存在着大量的悖论:-)
...
在这里,不受宠的特维尔和玛特斯塔塔有一座悖论之山 :-)
为什么概率论和Matstatistics 在这里突然变得不受欢迎?似乎他们在这里很好。但是用基于概率论和数学问题的废话。
悖论是什么?
爱因斯坦和GTR/STO,这总体上是很酷的。
"有一只巨大的蟾蜍以0.97C的速度向你飞来,你能猜出这是一只蟾蜍吗?"
为什么概率论和Matstatistics在这里突然不受重视了?他们在这里似乎很好。但基于概率论和数学统计学的胡说八道也有问题。
悖论是什么?
在MT4中,是否可以按照被测试时间的降序自动测试EA? 例如从2015.01.01到2015.12.31,下一步从2015.01.02到2015.12.31,以此类推。
我通过使用优化器来解决这个问题。
//+------------------------------------------------------------------+ // Внешние переменные input bool CheckEvery_Day=false; input bool TestEachYearSeparately=false; input int DayOfYear_=1; input int Year_=2009; // Эксперт функция тик void OnTick(void) { if(CheckEvery_Day) { if(TestEachYearSeparately) if(Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_) || Year()>Year_) return; //тестировать каждый год отдельно else if(Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_)) return; //тестировать весь период } // Ваш код } //+------------------------------------------------------------------+
选择一个时间段。
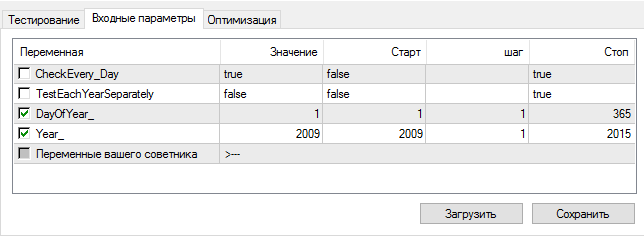
开启优化器。
我们得到的结果是,你可以看到专家顾问每次从新的一天开始是如何通过测试的。
为什么概率论和Matstatistics在这里突然不受重视了?他们在这里似乎很好。但基于概率论和数学统计学的胡说八道也有问题。
还有什么悖论?
这是你第一次听说电视和MC的悖论吗?
在这里,请看一下。有很多好的例子。
Sekai G / 概率论和数理统计中的悖论
类别:数学 2010年3月11日标题: 概率论和数理统计中的悖论
作者: Sekei G.
摘要: 匈牙利数学家的一本书,其中收集了概率论、数理统计和随机过程理论中的一些意想不到的结论和陈述。 这本书写得很生动,很吸引人,其中介绍的材料可用于大学概率论讲座中的说明,也可用于学校数学界工作的一些章节。
适用于各种资格的数学家,适用于所有概率论和数理统计的学生
pdf格式下载 (11,4 MB ):Sekey G. / 概率论和 数理统计中的悖论
vixri.com.
这是你第一次听说电视和MS的悖论吗?
看看吧。有很多好的例子。
Secei G / 概率论和数理统计中的悖论
类别:数学 2010年3月11日标题: 概率论和数理统计中的悖论。
作者: Sekei G.
摘要:匈牙利数学家的这本书,包含了概率论、数理统计和随机过程理论的意外发现和陈述。 它的写作方式生动有趣,其中的材料可用于大学概率论讲座的说明,而有些章节可用于学校数学圈的工作。
适用于各种资格的数学家,适用于所有概率论和数理统计的学生
pdf格式下载 (11,4 MB ):Sekey G. / 概率论和 数理统计中的悖论
vixri.com.
然后自己的东西是能用自己的话来写,还是只能在链接上,和截图上写?
我只是跑去看了一本书。这些悖论大多源于作者的无知,源于对问题的不正确表述。你必须打开你的眼睛和头脑,没有任何悖论。


全能的悖论。
这个悖论通常被表述为一个问题:"一个神能创造出他自己都搬不动的石头吗?"(我想是的,创造和提升的无限循环)或
"上帝能否创造一个内角总和不是180度的三角形?"(我想是的,黎曼几何)。
如果有人问哥伦布:"有可能在24小时内从欧洲到达美洲吗?"我想以当时的可能性,他肯定会说不可能,但现在任何孩子都会说有可能。 接下来的问题是:"这种可能性在哥伦布的时代已经存在,还是在我们的时代才出现?"从理论上讲,这种可能性一直存在,但在实践中,它只是在今天才得以实现。 是否可以由此得出结论:凡是不违背数学的东西都是可能的,无论我们是否能在物理上实现它?无论我们是否意识到,可能性都存在。