致作者(不知为何没有昵称)。
同样的问题可以用其他方法解决。可以对冗余变量和缺失变量进行测试。我可以这样做,然后与你的结果进行比较。但我需要你们所有的 .csv 格式文件。
我认为源文件在 masterdata.zip 压缩包中。
在选定变量后,我们必须将它们建立某种关系,其中价格是因变量(函数),其他指标是自变量。下面是示意方程:
价格 price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1表示前一个值。这很自然,因为该指标是从价格中分析得出的。考虑到价格是一个增量,因此我们将取指标的增量。由于懒惰,我没有取所有指标。让我们用最小二乘法来估计这个方程:
我们得到了方程系数的估计值。最后一列非常有趣:它表示相应系数等于零的概率。所有系数的这一概率都远高于至少 10%,也就是说,我们可以认为无法拒绝相应系数等于零的假设。因此,R 方的值非常离谱。
我的结论是,处理指标分类是无用的--它们是无用的,因为它们与价格增量毫无关系。
还是我错了?
......还是我错了?
我想你是对的 :-)
faa1947, 我有一个问题要问你。 我想澄清几件事...我是这样根据您的方程式计算数据的:
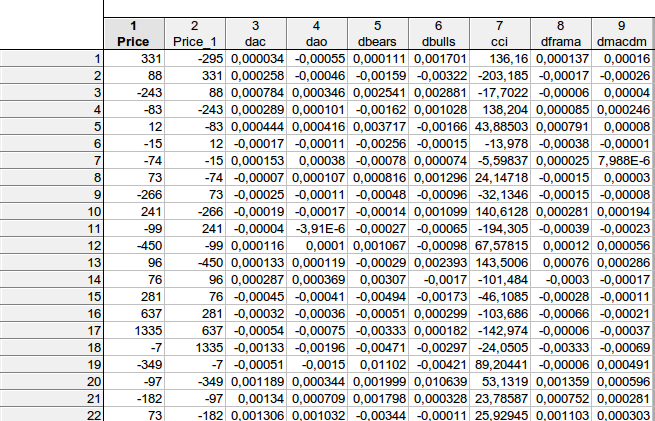
表格中的数据是否与您的示意方程相符price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
结果如下
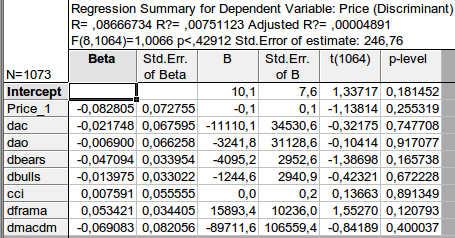
一旦我们选择了变量,就必须将它们建立某种关系,其中价格是因变量(函数),其他指标是自变量。下面是示意方程:
价格 price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1表示前一个值。这很自然,因为该指标是从价格中分析得出的。考虑到价格是一个增量,因此我们将取指标的增量。由于懒惰,我没有取所有指标。让我们用最小二乘法来估计这个方程:
我们得到了方程系数的估计值。最后一列非常有趣:它表示相应系数等于零的概率。所有系数的这一概率都远高于至少 10%,也就是说,我们可以认为无法拒绝相应系数等于零的假设。因此,R 方的值非常离谱。
我的结论是,处理指标分类是无用的--它们是无用的,因为它们与价格增量毫无关系。
还是我错了?
请提供您使用的统计方法的名称。是构建线性回归方程,输入是指标,输出是未来价格?是否正确?这不适用于外汇,因为它不是线性确定系统。判别分析的任务不同,它根据系统的外部描述建立模式识别模型。
如果对指标进行分类以分析价格增量毫无用处,那么技术分析就毫无意义了。幸运的是,价格的行为并不混乱,它对以前的事件有记忆。
看来你是对的 :-)
faa1947, 我有一个问题要问你。 我想澄清几件事...我是这样根据您的公式计算数据的:
表格中的数据是否与您的示意方程相符price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
结果如下:
原始数据如下:
方程如下
估计方程:
=========================
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
代入系数:
=========================
price = -0.0228102658125*price(-1) + 12005.8974278*dac(-1) + 4033.10946937*dao(-1) + 3176.11232129*dbears(-1) - 6021.36196728*dbulls(-1) - 0.102710105369*cci(-1) - 11487.4273249*dframa(-1) + 62535.3387412*DMACDM(-1)
我不明白您的计算方法。我的原则是使用滞后值(前值)。这样就可以进行预测。如果滞后-1 对应于第一个观测值,那么因变量就对应于一个新的、预测的、未观察到的观测值。
什么是 p 级?对我来说,就是相应系数为零的概率。
请提供所用统计方法的名称。是输入是指标,输出是未来价格的线性回归方程吗?是否正确?
回归是用最小二乘法估算的。它可以用来进行预测。
这对外汇无效,因为它不是线性确定系统。
如果是线性的,那也是在一个特定的例子中。它不是确定性的,因为即使是系数也被视为随机变量。所有系数都不是计算出来的,而是估计出来的。第二栏显示的是系数估算的标准误差。 请注意,这个误差非常大。
如果用于分析价格增量的指标分类毫无用处,那么技术分析将毫无意义。
正是如此,而且我敢向您保证,不止我一个人这么认为。技术分析不是一门科学,而是一种占星术。最初,300 年前,它是一种可视化 Kotir 的系统。从那时起,它已经有了巨大的发展。其他一切都属于奇迹领域的皮诺切斯。我对你的文章很满意,因为它有一些规律性的、可重复的思考。
如果分析价格增量的指标分类毫无用处
在这里,我们分析了指标的一个特例。总是有必要证明某个指标或其使用与报价有关。TA 从不考虑这个问题。
幸运的是,价格的行为并不混乱,它对以前的事件有记忆。
所有计量经济学都建立在报价具有确定性成分(自相关性、记忆)和噪声的假设之上。
判别分析的任务不同,它根据系统的外部描述建立模式识别模型。
任务是明确的。但问题是,得到的结果是否可信。问题不在于分类(这是问题的一部分,也需要解决),而在于对预测结果的信任。这正是问题所在。
我不明白你的计算方法。我的原则是使用滞后值(前值)。这样就可以进行预测。如果滞后-1 对应于第一个观测值,那么因变量就对应于一个新的、预测的、未观察到的观测值。
什么是 p 级?对我来说,就是相应系数为零的概率。
faa1947,我给出了带有滞后期的表格(前几行--我无法拟合整个表格)。然后,我将因变量Price 向前移动了一步。
结果发现,在第一行的示例中
331 =C(1)*(-295) + C(2)* 0.000034+ C(3)* (-0.00055) + C(4)* 0.000111 + C(5)* 0.001701+ C(6)*136.16+ C(7)* 0.000137+ C(8)*0.00016, 条件是
price = C(1)*price(-1) + C(2)*dac(-1) + C(3)*dao(-1) + C(4)*dbears(-1) + C(5)*dbulls(-1) + C(6)*cci(-1) + C(7)*dframa(-1) + C(8)*dmacdm(-1)
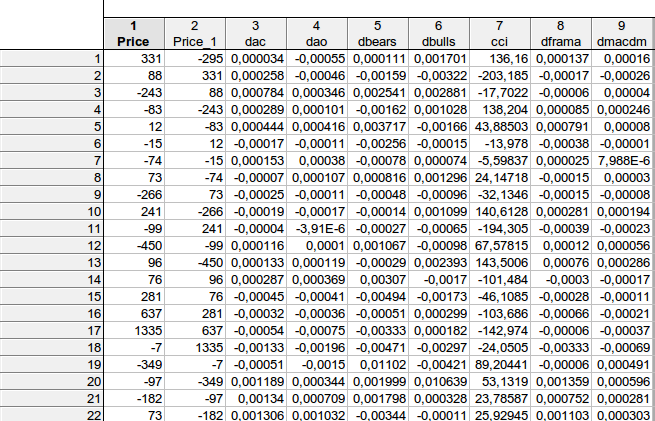
总的来说,我大致得到了类似的结果 - 无法拒绝 所考虑的系数等于零的零假设...
新文章 利用判别分析开发交易系统已发布:
开发交易系统时,通常都会出现选择最佳指标与信号组合的问题。而判别分析就是找到此类组合的方法之一。本文会给出一个用于市场数据采集的 EA 开发示例,并详细阐明如何利用判别分析在 Statistica 软件中构建外汇市场预后模型。
作者:ArtemGaleev