Здравствуйте уважаемые профессионалы!
Может кто подскажет, как ухватить разброс?
В таблице разные волны, как захватить их по отдельности. допустим это пять волн
Здравствуйте уважаемые профессионалы!
Может кто подскажет, как ухватить разброс?
В таблице разные волны, как захватить их по отдельности. допустим это пять волн
смотришь слева-направо и ближайшие по расстоянию (dX^2+dY^2) отметки соедининяются линией. Если известно что "волны" предпочитают "вниз" - соотв.корректировка критерия
смотришь слева-направо и ближайшие по расстоянию (dX^2+dY^2) отметки соедининяются линией. Если известно что "волны" предпочитают "вниз" - соотв.корректировка критерия
Хмм
Я перебираю по диагонали
for(int pu=2; pu< nb.m_pmax; pu++) { for(int p = pu, b = nb.m_rt-1; p >= pu-p-1 && b >= nb.m_rt-nb.m_pmax; p--, b--) Svjazka0_2(p,b,pu,tf); // проверяем значение, если >0, то фиксируем } for(int pu=nb.m_rt-2, o=nb.m_pmax/2; pu >nb.m_rt-nb.m_pmax; pu--, o++) { for(int p = nb.m_pmax-1, b =pu; p >= o; p--, b--) Svjazka0_2(p,b,pu,tf); // проверяем значение, если >0, то фиксируем }
Если можно как то поподробней, что подразумевает :
Вы предлагаете использовать элемент,
dX = x2 - x1, dY = y2 - y1
dX^2+dY^2
Здравствуйте уважаемые профессионалы!
Может кто подскажет, как ухватить разброс?
В таблице разные волны, как захватить их по отдельности. допустим это пять волн
Хмм
Я перебираю по диагонали
Если можно как то поподробней, что подразумевает :
Вы предлагаете использовать элемент,
dX = x2 - x1, dY = y2 - y1
dX^2+dY^2
представь плоскость по которой были прочерчены некоторые почти-паралельные, непересекающиеся плавные кривые, потом что-то там стряслось, связи потерялись и что-то затёрлось. Надо восстановить связность.
самый простой алгоритм: от точки обрыва смотришь - которая из неразмеченных точек ближе, та видимо и продолжение линии. Переходишь к ней и так далее.
полученный результат тоже возможно потребует обработки (особенно если изначально линии проходили близко)
представь плоскость по которой были прочерчены некоторые почти-паралельные, непересекающиеся плавные кривые, потом что-то там стряслось, связи потерялись и что-то затёрлось. Надо восстановить связность.
самый простой алгоритм: от точки обрыва смотришь - которая из неразмеченных точек ближе, та видимо и продолжение линии. Переходишь к ней и так далее.
полученный результат тоже возможно потребует обработки (особенно если изначально линии проходили близко)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
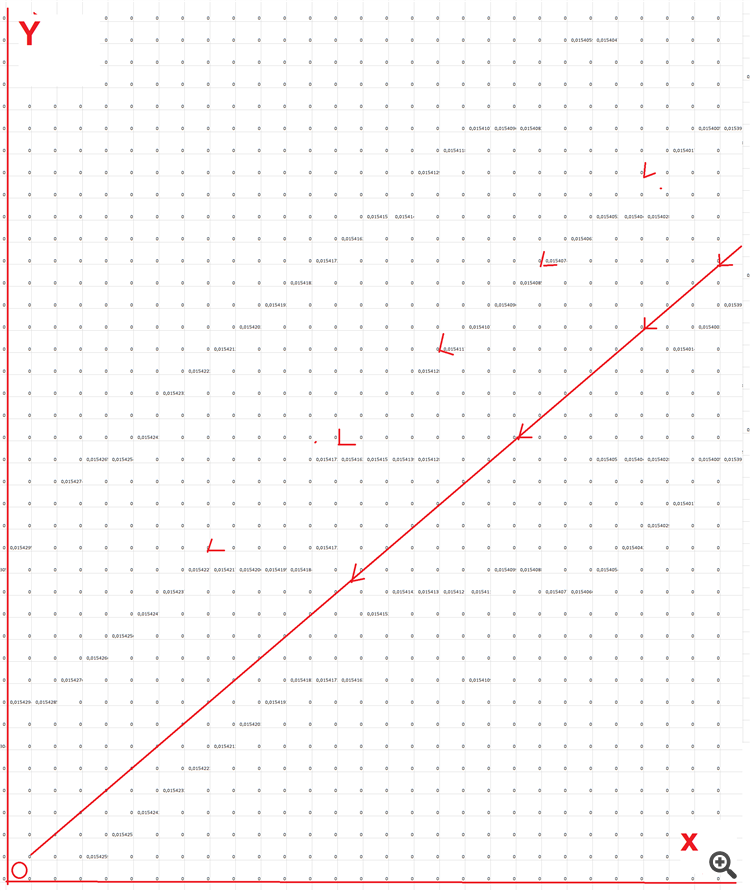
Здравствуйте уважаемые профессионалы!
Может кто подскажет, как ухватить разброс?
В таблице разные волны, как захватить их по отдельности. допустим это пять волн