Решение системы M линейных уравнений с N неизвестными
Подставив ваши значения получаем ответ: Заданная система уравнений имеет множество решений.
Что-то туплю, вроде как решений нет. вот система (знак системы не ставлю).
x8-x7=x4-x1
x9-x8=x5-x2
x10-x9=x6-x3
x7=x1+x2+x3
x8=x2+x3+x4
x9=x3+x4+x5
x10=x4+x5+x6
x7=8
x8=4
x9=3
x10=-3
найти x1,x2,x3,x4,x5,x6
первое плюс четвертое уравнение дают пятое
аналогично (2)+(5) ->(6) и (3) + (6)->(7)
то есть 5, 6 и 7 уравнения новых данных не дают. Для остальных решений бесконечно много
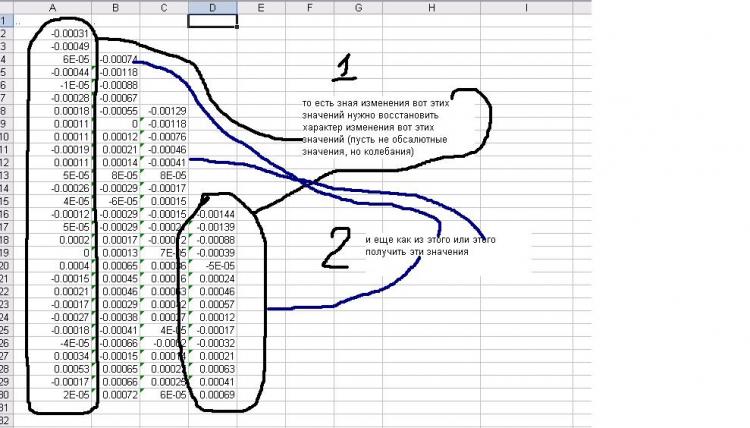
хреново)))))спасибо за ответ. я это к чему все затеял- нужно было восстановить ряд по суммарным значениям этого ряда. щас файл прикреплю.
Чтобы система уравнений имела одно решение, нужно, чтобы количество уравнений было равно или больше количества неизвестных, и уравнения были бы, при этом, разные.
да в курсе я про число уравнений и количество неизвестных (условие). увязать то как первый столбик с последним, может корень золотой твой тут поможет?
а вы знаете какой у меня родной язык? я нет, но догадываюсь, хотя и тут могу ошибаться.
следуя вашей системе деления на имеющих право и нет, можно также с легкостью выдать, что сварщик не имеет права размножаться, потому что не знает законов обольщения.
Чтобы система уравнений имела одно решение, нужно, чтобы количество уравнений было равно или больше количества неизвестных, и уравнения были бы, при этом, разные.
Не разные, а линейно независимые.
Напомню общеизвестные из любого курса матричной алгебры факты.
Система линейных уравнений, в которой ни одно из уравнений не является линейной комбинацией остальных:
- имеет ровно 1 решение, если число неизвестных равно числу уравнений;
- имеет бесконечное число решений, если число неизвестных больше числа уравнений ( недоопределённая система );
- не имеет ни одного решения, если число неизвестных меньше числа уравнений ( переопределённая система ).
Во втором и третьем случае, однако, существует (не)единственное приближённое решение в смысле минимума некоторой нормы. :)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Что-то туплю, вроде как решений нет. вот система (знак системы не ставлю).
x8-x7=x4-x1
x9-x8=x5-x2
x10-x9=x6-x3
x7=x1+x2+x3
x8=x2+x3+x4
x9=x3+x4+x5
x10=x4+x5+x6
x7=8
x8=4
x9=3
x10=-3
найти x1,x2,x3,x4,x5,x6