Não vejo um atraso no muving. Isso significa que o autor não entende o que ele definiu, ou há um erro no algoritmo e no indicador de refiles.
Não há nenhum atraso, pois não é um muwink em geral. O problema de minimizar a função para uma determinada série é resolvido. Claro que quando a série está em movimento, se o comprimento da série for pequeno, ela redesenhará quando novas informações aparecerem, especialmente se houver espigões. Descrição do filtro em http://en.wikipedia.org/wiki/Hodrick-Prescott_filter
Em princípio, esta função está em MATLAB, se não me engano, ela pode ser transformada em uma DLL usando o compilador Matlab. Assim, crie um indicador que aborde este Dll.
Eu acho que o mundo é mais simples do que com uma dll.
Aqui está a função que precisamos minimizar para construir este filtro digital:
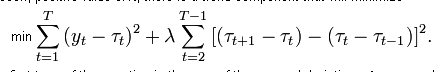
Podemos ver que nesta formulação o filtro só pode trabalhar com dados históricos, pois para calcular o valor da linha de tendência no momento atual precisamos conhecer não só os valores anteriores desta tendência, mas também um passo à frente t[i+1]. Tal filtro, na história, mostrará a coincidência exata da curva suave com o kotir (isto é o que o autor citou no primeiro post como uma demonstração), enquanto que na borda direita do kotir haverá um inacreditável sobre-estiramento.
Eis o que mais eu desenterrei na web:
Não consegui encontrar nenhuma receita pronta para a construção deste filtro. Na verdade, vamos tomar e construir um funcional para a margem direita da BP por nós mesmos (equação superior).
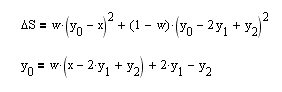
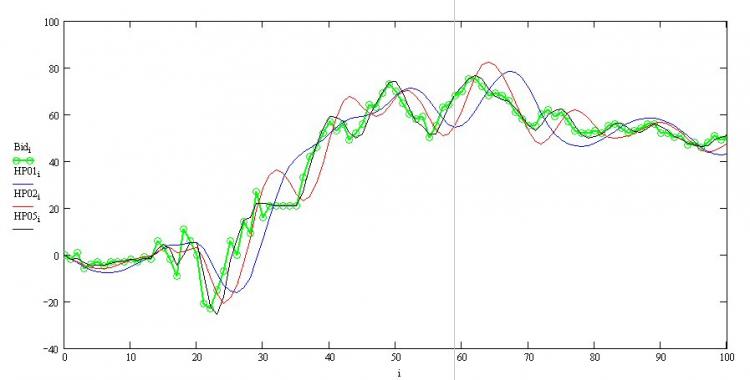
Vamos pegar uma derivada dela pelo parâmetro y[0] - valor atual e igualá-la a zero, e imediatamente obter uma expressão recorrente para o filtro HP necessário (equação inferior). Vamos ver como as propriedades de suavização do filtro dependem do parâmetro de suavização w:
Aqui, a linha verde é mais grossa, a linha preta é w=0,5, etc. Você pode ver que tudo funciona corretamente - há um inevitável atraso de fase que é maior quanto mais forte for o antialiasing e a borda direita não for redesenhada. Agora podemos codificá-lo também em MQL.
//+------------------------------------------------------------------+
//| Moving Average HP.mq4 |
//| Code by Neutron |
//+------------------------------------------------------------------+
#property indicator_chart_window
#property indicator_color1 Blue
#property indicator_width1 3
extern double w=0.1;
int Start,i,m;
double MA[5000],Y[5000];
int start()
{
Start=5000;
MA[Start]=Open[Start];
MA[Start-1]=Open[Start-1];
for (i=Start-2;i>=0;i--) MA[i]=w*(Open[i]-2.*MA[i+1]+MA[i+2])+2.*MA[i+1]-MA[i+2];
}
int init()
{
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,MA);
return(0);
}
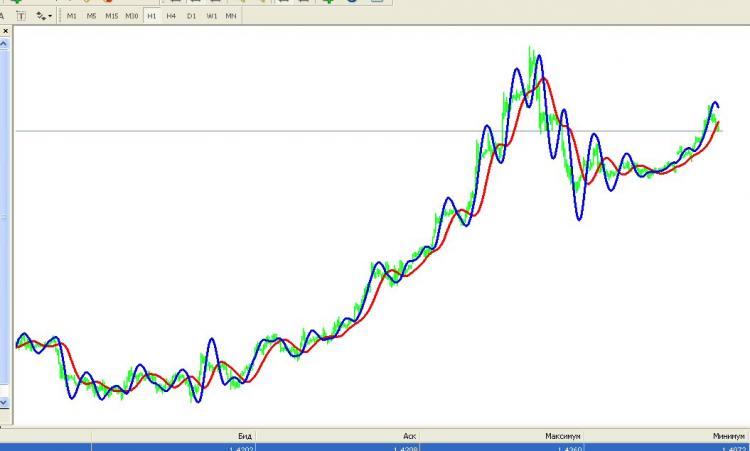
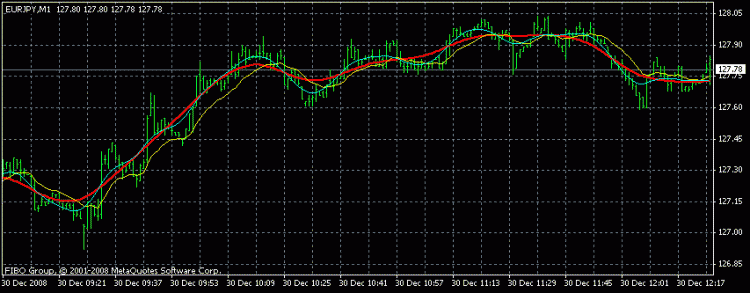
Eis o resultado:
Azul é HP, verde é cotier, vermelho é um filtro Watterout de 2ª ordem (para comparação).
De fato, este filtro tenta capturar as tendências lineares honestamente. Veja a funcionalidade no topo do posto - mostra que além de minimizar o desvio do kotir (primeira soma), há uma exigência de minimizar a segunda derivada (segunda soma)! E afinal, a segunda derivada da linha é zero, e a exigência de minimizá-la é igual à exigência de maximizar a aspiração à linha de tendência para um vetor de entrada de dados arbitrário. Eu gostei da abordagem.
P.S. É interessante, se na expressão para que o funcional exija a minimização da primeira derivada (a equação superior) ao invés da segunda, obtemos uma fórmula de recorrência muving para a EMA média exponencial (a equação inferior):
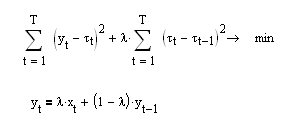
Acontece que a média exponencial é a mais lisa de todas as unidades possíveis!
Acontece que a média exponencial é a mais suave de todas as mutilações possíveis.
Sim, há um artigo sobre o assunto.
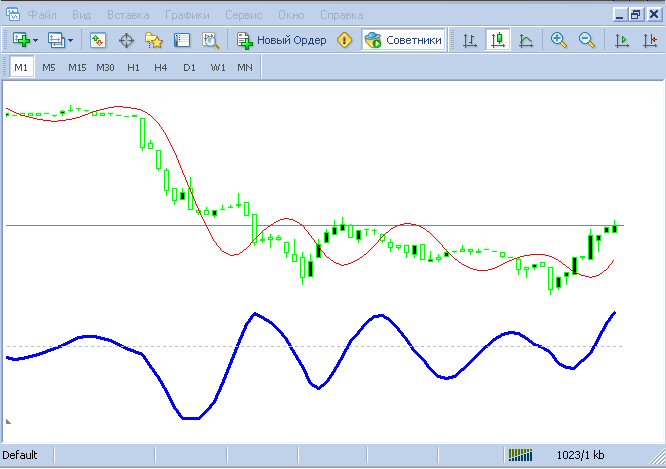
Ainda não fiz sobre o artigo, mas desenvolvendo a mesma idéia de suavidade de ema você pode obter uma boa lisura:
Azul - EMA15 com um atraso de 5.
Vermelho - MA mais suave com o mesmo atraso.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso

Olá, caros programadores!
Quem se encarregará de resolver, penso eu, uma simples tarefa de escrever um indicador? Preciso escrever um indicador que filtre a série com o filtro Hodrick-Prescott. A função está disponível no MATLAB, se não estou enganado, ela pode ser transformada em uma DLL usando o compilador MATLAB. Por conseguinte, precisamos criar um indicador, que se dirija a este Dll. Na entrada, devemos alimentar os seguintes parâmetros - comprimento de série, parâmetro de suavização. A saída é um componente de tendência (a ser desenhado no gráfico) e um componente cíclico (oscilador).
Não posso fazer isso sozinho; não conheço o MATLAB Compiler e o MQL4.
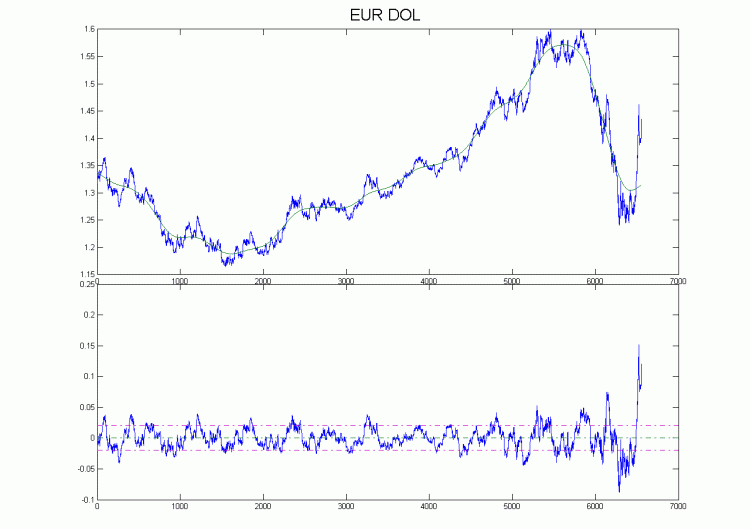
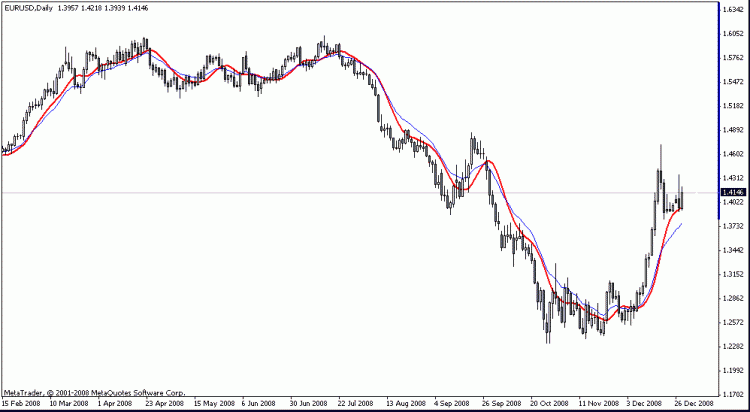
Tenho uma decomposição para o Eurodollar H4 na tabela. Como visto quase ao longo da história, a peculiaridade do movimento de preços era que, depois de quebrar a tendência, o preço se movia para uma distância igual à diferença entre o extremo anterior e a tendência, em suma, a amplitude era quase a mesma. A exceção são os dados mais recentes, mas são extremos lá. Basicamente, tal indicador deve ser redesenhado se o número de pontos de dados for pequeno; no entanto, se eles forem aumentados, digamos, até 2000, não surgirão problemas com o redesenho.