Discussão do artigo "Combinatória e teoria da probabilidade para negociação (Parte II): fractal universal"
Se for possível, peço ao autor deste artigo que considere os seguintes argumentos:
Até agora, vejo que o princípio da proporção áurea pode ser usado para construir cadeias fractal-probabilísticas formando um grupo completo de eventos, mas sinceramente não vejo o que essa abordagem pode proporcionar. Parece que a proporção áurea também está conectada à série fibo, mas, novamente, não vejo como ela pode ser aplicada e para que, se você tiver ideias que possa escrever aqui, acho que será uma vantagem. E assim, em geral, esses processos já se formaram em minha cabeça, em geral isso é tudo o que é necessário para derivar fórmulas mais complexas. Até o momento, os fractais obtidos cumprem sua tarefa. Lá, tudo vai do complexo ao simples e assim por diante. Posso pensar na aplicação da proporção áurea, mas não consigo ver como isso será útil. Série fibo também, todo mundo diz fibo-fibo ... Ololo, eles ouvem uma palavra inteligente e a repetem como um papagaio. Eu sempre parto do fato de que um princípio matemático corresponde a um problema específico e sempre encontro uma solução para qualquer problema depois de algum tempo. A ferramenta da solução é selecionada no processo, o próprio cérebro a encontra e, se possível, encontra semelhanças com algo que está no ouvido. Em outras palavras, primeiro determinamos o que precisamos encontrar e depois procuramos maneiras de resolver o problema. Eu estaria mais interessado em ouvir problemas específicos, e você pode criar um artigo separado com essas soluções, seria interessante e divertido, eu acho. Dentro da estrutura desses problemas, podemos aplicar a proporção áurea e qualquer outra coisa, desde que o resultado seja realmente necessário e traga um benefício concreto para alguém. Portanto, você pode escrever sugestões.
Se for possível, peço ao autor deste artigo que considere os seguintes argumentos:
Esse é apenas um mito banal de supostos fibo e ZS em todos os lugares....
O engraçado é que, se você pegar qualquer pote e torcê-lo bem, poderá encontrar nele tanto o fibo quanto a proporção áurea, o pi, o e e muitas outras coisas....
É apenas um mito banal de supostamente fibo e ZS em toda parte e em qualquer lugar...
O engraçado é que, se você pegar qualquer pote e girá-lo bem, poderá encontrar nele o fibo, a proporção áurea, o número de pi, o número de e e muitas outras coisas....
Os fibos (eles também são a proporção áurea, o que muitas pessoas não percebem) são procurados, ou seja, vistos, com extrema facilidade. Porque elas são exponenciais. Que, por sua vez, são somas... Em geral, você pode contar coisas elementares da escola há muito tempo (!!!), mas isso é inútil.
Você também pode fazer isso dessa forma:
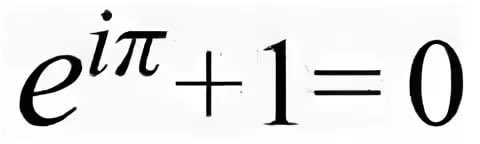
lindo, misterioso... a conexão de FIBO com Fourier... as constantes mundiais em um copo... e outras coisas.
É apenas um mito banal de supostamente fibo e ZS em toda parte e em qualquer lugar...
O engraçado é que, se você pegar qualquer pote e torcê-lo bem, poderá encontrar nele o fibo, a proporção áurea, o número de pi, o número de e e muitas outras coisas....
você também pode encontrar a cabeça e os ombros no pote se o colocar em sua cabeça).
É apenas um mito banal de que Fibo e ZS estão em toda parte e em todos os lugares....
O engraçado é que, se você pegar qualquer pote e torcê-lo bem, poderá encontrar nele o fibo, a proporção áurea, o pi, o e e muitas outras coisas....
Eu não poderia concordar mais)) É realmente verdade. Os traders gostam muito de procurar um significado oculto onde não há nenhum). Estou tentando transmitir a mesma coisa cuidadosamente às pessoas, mas não sei como fazer isso sem dizer a verdade, e a verdade é cruel). Cheguei à conclusão de que há um problema e há um conjunto de soluções possíveis, e qualquer outra coisa além disso é perda de tempo. Para obter uma solução, você deve primeiro definir claramente o problema e ter pelo menos uma ideia superficial das possíveis maneiras de solucioná-lo. Se não houver tais maneiras, então começa o que foi dito acima, Fibonacci, as fórmulas de Euler e outras coisas muito bonitas, mas tão inúteis que você involuntariamente começa a ler nas entrelinhas. Cada ferramenta tem sua própria tarefa. Com relação a isso, proponho ir direto aos detalhes (tarefas específicas).
Até o momento, vejo que o princípio da proporção áurea pode ser usado para construir cadeias de probabilidade fractal que formam um grupo completo de eventos, mas sinceramente não vejo o que essa abordagem pode fazer. Parece que a proporção áurea também está conectada à série fibo, mas, novamente, não vejo como ela pode ser aplicada e, se você tiver ideias que possa escrever aqui, acho que será uma vantagem. E assim, em geral, esses processos já se formaram em minha cabeça, em geral isso é tudo o que é necessário para derivar fórmulas mais complexas. Até o momento, os fractais obtidos cumprem sua tarefa. Lá, tudo vai do complexo ao simples e assim por diante. Posso pensar na aplicação da proporção áurea, mas não consigo ver como isso será útil. Série fibo também, todo mundo diz fibo-fibo ... Ololo, eles ouvem uma palavra inteligente e a repetem como um papagaio. Eu sempre parto do fato de que um princípio matemático corresponde a um problema específico e sempre encontro uma solução para qualquer problema depois de algum tempo. A ferramenta da solução é selecionada no processo, o próprio cérebro a encontra e, se possível, encontra semelhanças com algo que está no ouvido. Em outras palavras, primeiro determinamos o que precisamos encontrar e depois procuramos maneiras de resolver o problema. Eu estaria mais interessado em ouvir problemas específicos, e você pode criar um artigo separado com essas soluções, seria interessante e divertido, eu acho. Dentro da estrutura desses problemas, podemos aplicar a proporção áurea e qualquer outra coisa, desde que o resultado seja realmente necessário e traga um benefício concreto para alguém. Portanto, você pode escrever sugestões.
1. Talvez todo mundo já tenha ouvido falar desse "ololo", mas eu não escrevi sobre fibo, porque não aconselho "puxar" os níveis de fibo, embora, se forem calculados corretamente, possam ser usados, mas em combinação com as ondas de Elliott.
É claro que isso não é tudo, você sabe o quanto esse trabalho é demorado e meticuloso, mas comecei este tópico por um motivo. Tentarei fazer tudo o que depender de mim e, em geral, essas questões, para ser honesto, deveriam ser tratadas por toda uma equipe de matemáticos e programadores, se não por todo um instituto. O que uma pessoa pode fazer contra isso? Mesmo que você tenha um supercérebro, há tantos dados para processar que você pode enlouquecer. Estou tentando definir as tarefas que são proporcionais ao meu tempo e às minhas capacidades, sim, posso fazer mais, mas isso não depende de mim agora. O tempo é o recurso mais valioso. Se houvesse pessoas interessadas em análises complexas e dedicação total, eu ficaria feliz em fazer isso. No entanto, o ramo continuará e eu cobrirei o material que puder, sempre tentando contar algo novo, na medida do possível.
O mito sobre a universalidade da proporção áurea na natureza cresceu tanto que as pessoas nem se preocupam com verificações reais, sucumbindo aos encantos da beleza da própria ideia da proporção entre o todo e suas partes, mas na verdade não é assim:
- as conchas de moluscos-nautilus (que geralmente são ilustradas em artigos sobre a magia do WD), ao contrário da opinião popular, não correspondem ao WD.
- As proporções de um corpo humano do famoso desenho "Homem Vitruviano" de Leonardo Da Vinci não são observadas em relação a pessoas reais.
- O Partenon, as pirâmides e outros objetos correspondem de forma muito imprecisa à RS (desenhada por amantes do misticismo).
- Pesquisas psicológicas objetivas com a finalidade de revelar se o QE é a base da percepção da beleza fracassaram com sucesso.
- Por fim, os testes quantitativos de quebra/rejeição de níveis na negociação também não mostram que o QE é algo particularmente importante.
A única razão pela qual os mercados podem, às vezes (palavra-chave OUTRA VEZ), recuar/quebrar os níveis de fibo é devido à crença coletiva de um grande número de operadores técnicos nos níveis de fibo (uma profecia autorrealizável) se eles colocarem coletivamente seus stops/limites lá, mas mesmo isso provavelmente não funcionará porque os participantes profissionais, os grandes operadores institucionais, negociarão em outra base, e o rompimento/reversão do nível Fibo pode ser apenas aleatório, mas para quem acredita no QE certamente será uma confirmação de sua fé.
Keith Devlin, professor de matemática da Universidade de Stanford, explica isso de forma simples: "..... A maioria das pessoas não entende de matemática e não consegue nem mesmo entender como uma fórmula como a proporção áurea se aplica a um sistema complexo, portanto, elas também não podem se testar. As pessoas acham que veem a proporção áurea em toda parte, na natureza e em seus objetos favoritos, mas não conseguem comprovar isso. Elas são vítimas de seu desejo natural de encontrar significado nos vários objetos do universo, mas, devido à falta de conhecimento matemático, não conseguem perceber que os padrões que detectam são ilusórios."
As pessoas se programam (zumbis) para encontrar uma explicação simples e se esforçam para manter essa crença, essa é a essência do pensamento religioso, inclusive no comércio...
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Combinatória e teoria da probabilidade para negociação (Parte II): fractal universal foi publicado:
Neste artigo, continuaremos a estudar fractais e prestaremos muita atenção a resumir todo o material. Tentarei apresentar todos os projetos da maneira mais compacta e compreensível para serem aplicados ao trading.
Começaremos pegando as regras de construção que estabeleci no artigo anterior e complementando-as para compreender plenamente como é construído um fractal. Adicionalmente, convém mencionar que notei um pequeno erro, nas minhas fórmulas, que não permitia conseguir a assimetria das bordas tanto para cima quanto para baixo. Porém, deduzi as fórmulas de forma correta e elas funcionam para qualquer fractal. E, na verdade, consegui obter uma função para a implementação de qualquer fractal. Todos os fractais possíveis são um caso especial de um fractal geral. Se tomarmos os três tipos de fractais que defini acima, verifica-se que as condições do fractal geral para a implementação destes três casos especiais assumirão a forma:
Esses três tipos de fractais podem ser representados como um esquema:
Idealmente, "S" deve tender para o infinito. Não descrevi as variáveis a seguir no artigo anterior, mas vou fazer isso aqui para obter uma visão ampla de como usar a fórmula geral para obter casos especiais. Um fractal é uma função que opera com base no princípio de reação em cadeia, como acontece com uma bomba atômica. Se definirmos uma reação em cadeia com muita profundidade, o computador poderá não ser capaz de lidar com os cálculos, no melhor dos casos, ele simplesmente ficará processando tais cálculos por um longo tempo, quer em questão de minutos, horas ou até dias.
Autor: Evgeniy Ilin