Yury Kirillov / 프로필

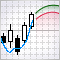
이번 글에서는 이전 글에서 만든 인디케이터를 한층 업그레이드해 보고, 부트스트랩과 분위수를 이용한 예측 신뢰 구간 측정 방법에 대해서도 간단하게 알아보겠습니다. 예측 인디케이터 개발과 예측 정확도 측정에 사용될 스크립트 작성이 목표입니다.

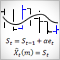
이 문서를 통해 시계열의 단기 예측에 사용되는 지수 평활 모형을 독자분들이 익숙해지실 수 있도록 설명해드릴 것입니다. 또한 예측 결과의 최적화 및 추정과 관련된 주제를 다루고, 스크립트와 인디케이터를 예시삼아 몇 가지 제공해드릴 것입니다. 이 문서는 지수 평활 모형에 기초한 예측 원칙을 처음 숙지하는 데 유용할 것입니다.

이 문서를 통해 다양한 시계열의 특성에 대한 빠른 예비 추정치를 제공하기 위해 고안된 클래스를 소개해드릴 것입니다. 이 경우 통계적 모수와 자기 상관 함수가 추정되고 시계열의 스펙트럼 추정이 수행되며 히스토그램이 작성됩니다.

대부분의 수학적 모델과 방법은 서로 다른 가정을 기반으로 하기 때문에 시퀀스의 통계적 모수 추정은 매우 중요합니다. 예를 들어 분포 법칙의 정규성이나 분산 값 또는 기타 모수가 있습니다. 따라서 시계열 분석 및 예측 시 주요 통계 모수를 빠르고 명확하게 추정할 수 있는 간단하고 편리한 도구가 필요합니다. 이 문서는 랜덤 시퀀스의 가장 간단한 통계적 모수와 시각적 분석의 여러 메소드에 대해 설명할 것입니다. MQL5에서는 이러한 방법의 구현과 Gnuplot 애플리케이션을 사용한 계산 결과의 시각화 메소드를 제공합니다.

오늘날에는 웹 브라우저가 설치되어 있지 않은 컴퓨터를 찾기가 어렵습니다. 오랫동안 브라우저는 진화하고 개선되어 왔습니다. 이 문서에서는 브라우저에 표시하기 위해 MetaTrader 5 클라이언트 터미널에서 얻은 정보를 기반으로 차트와 다이어그램을 만드는 간단하고 안전한 방법에 대해 설명합니다.

이 글은 독자들이 MQL5 언어의 그래픽 객체를 사용하는 가능한 변형에 대해 알게 하기 위한 것입니다. 그래픽 개체를 사용하여 간단한 스펙트럼 분석기를 관리하는 패널을 구현하는 표시기를 분석합니다. 이 기사는 MQL5의 기본 사항에 대해 잘 알고 있는 독자를 대상으로 합니다.

이 글은 표시기 다시 그리기, 다중 시간대 표시기, 일본 캔들스틱 시세 표시에 대한 저자의 의견을 간략히 설명합니다. 이 문서에는 프로그래밍 관련 내용이 없으며 일반 문서입니다.

이 자료에서는 MetaTrader 클라이언트 터미널에서 사용할 수 있는 견적 표현의 몇 가지 특성을 분석하려고 합니다. 기사는 일반적이고 프로그래밍과는 무관합니다.

이 문서는 MQL4 언어 함수에 대한 간략한 가이드로, 프로그램을 MQL4에서 MQL5로 이전하는데에 도움을 드릴 것입니다. MQL4 함수마다 (거래 함수 제외) 설명과 대응하는 MQL5쪽의 구현이 적혀있어 이전하는데에 드는 시간을 눈에 띄게 줄여줄 것입니다.. 편의를 위해 MQL4 함수들은 MQL4 레퍼런스처럼 그룹별로 나뉘어있습니다.