푸리에 감정가 ..
수신 범위에 대한 주기적인 신호가 있다고 가정합니다.
결과 - 배열의 시작 - 주기적인 시퀀스의 연속입니다.. 그래서?
그럼 사진을 볼까요?
아래쪽 표시기에는 곡선(빨간색)이 있습니다. 녹색은 매개변수를 사용하여 변환 프로세스 중에 얻은 선입니다.
변환 창 크기 2^6=64 포인트, 사용 빈도 수 45.
저것들. 우리는 결과 곡선의 유사성을 얻습니다 .. 원본에 겹쳐집니다 ..
그림에서 알 수 있듯이 처음부터 끝까지 대체하십시오 - 이것은 실제 결과가 아닙니다 -
따라서 문제는 녹색 선으로 표시된 곡선의 움직임을 계속하는 방법입니다.
그렇다면 질문을 다른 방식으로 할 수도 있습니다.
곡선이 작은 영역에서 계속 움직일 수 있도록 그림에 표시된 함수를 어떤 식으로 근사화할 수 있습니까?
그럼 사진을 볼까요?
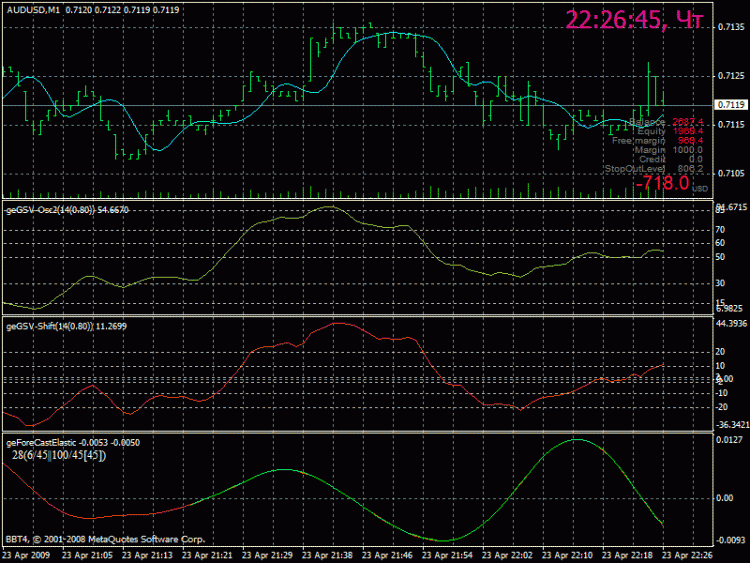
아래쪽 표시기에는 곡선(빨간색)이 있습니다. 녹색은 매개변수를 사용하여 변환 프로세스 중에 얻은 선입니다.
변환 창 크기 2^6=64 포인트, 사용 빈도 수 45.
저것들. 우리는 결과 곡선의 유사성을 얻습니다 .. 원본에 겹쳐집니다 ..
그림에서 알 수 있듯이 처음부터 끝까지 대체하십시오 - 이것은 실제 결과가 아닙니다 -
따라서 문제는 녹색 선으로 표시된 곡선의 움직임을 계속하는 방법입니다.
1. 근사를 위해 취한 64개의 점이 주기적 함수라고 결정한 이유는 무엇입니까?
2. 고조파의 수는 채취한 샘플의 절반을 초과할 수 없습니다. 근사값이 기간의 64분할이면 최대 고조파는 31번째가 됩니다.
3. 근사를 위해 비주기적 함수를 사용했기 때문에 비현실적인 결과가 나왔고, 따라서 기간의 연속이 일치하지 않습니다. 당신은 이미 PF가 주기적인 기능에만 효과적이며 다른 모든 것은 탬버린과 함께 춤을 추고 있다는 사실을 이미 알고 있습니다.
두 개의 동일한 기간을 취해야 합니다: 0 - 2*PI, 2*PI - 4*PI. 둘 다에 대해 PF를 구동하고 고조파의 진폭과 위상이 일치하는지 비교합니다. 그렇지 않은 경우 기능은 비주기적이며 기준 기간은 증가하거나 감소해야 합니다(감소 또는 증가 - 이는 개별 고조파에 대한 위상 변이를 이미 보고 있음).
, 다른 모든 것은 탬버린과 함께 춤을 추고 있습니다.
두 개의 동일한 기간을 취해야 합니다: 0 - 2*PI, 2*PI - 4*PI. 둘 다에 대해 PF를 구동하고 고조파의 진폭과 위상이 일치하는지 비교합니다. 그렇지 않은 경우 기능은 비주기적이며 기준 기간은 증가하거나 감소해야 합니다(감소 또는 증가 - 이는 개별 고조파에 대한 위상 변이를 이미 보고 있음).
원칙적으로 이것은 "탬버린과 함께 춤을 추는" 것이기도 하며, 더 "속임수를 당한" 것뿐입니다. 결과는 이야기의 "더 아름다운"그림이 될 것입니다. 그 이상은 아닙니다.
주기적은 모든 x에 대해 다음 평등이 true f (x) \u003d f (x + T)인 T가 있는 함수입니다. 그러면 T는 함수 f(x)의 주기입니다.
간단히 말해서, 거래자는 제안된 알고리즘에 따라 T 를 선택할 때(연속된 두 기간의 공배수로), 동일한 샘플 크기의 세 번째 기간이 선택한 값에 해당한다는 보장이 없습니다(세 번째 기간은 정확히 외삽이 이루어지는 기간). T를 선택하는 알고리즘에 대한 보장은 없습니다.
그런데 함수가 주기적이라면 이 푸리에가 포기한 이유는 무엇입니까? 아무도 생각하지 않았나요? 마침표를 찾고 값을 대체합니다. 그게 다에요.). 아 물론 생리를 하고 탬버린으로 춤을 추지 않았다면....
행운을 빕니다.
여보세요..
푸리에 변환에 대해 질문이 있습니다.
푸리에 변환 및 역변환 고역 통과 필터링 후,
변환 범위 외부에서 결과 함수의 계산을 계속해야 합니다(가능한 경우 예에서).