작성자에게(어떤 이유로 닉네임이 없음).
같은 문제를 다른 방법으로 해결할 수 있습니다. 중복 및 누락된 변수에 대한 테스트가 있습니다. 그렇게 해서 여러분의 결과와 비교해 볼 수 있습니다. 하지만 .csv 형식의 모든 파일이 필요합니다.
소스는 마스터데이터.zip 아카이브에 있는 것 같습니다.
변수를 선택한 후에는 가격이 종속 변수(함수)가 되고 다른 지표가 독립 변수가 되는 관계를 만들어야 합니다. 다음은 개략적인 방정식입니다:
가격 가격(-1) DAC(-1) Dao(-1) DBARS(-1) DBULLS(-1) CCI(-1) DFAMA(-1) DMACDM(-1)
-1은 이전 값을 의미합니다. 이는 지표가 가격에서 분석적으로 파생되었기 때문에 자연스러운 현상입니다. 가격이 증분이라는 점을 고려하여 지표의 증분을 취하겠습니다. 게으름 때문에 모든 지표를 취하지는 않습니다. 최소제곱법으로 이 방정식을 추정해 봅시다:
방정식 계수의 추정치를 얻었습니다. 마지막 열은 매우 흥미롭습니다. 해당 계수가 0과 같을 확률을 의미합니다. 모든 계수에 대한 이 확률은 최소 10%보다 훨씬 높습니다. 즉, 해당 계수가 0이라는 가설을 거부할 수 없다는 것을 고려할 수 있습니다. 따라서 R- 제곱은 우스꽝스러운 값을 갖습니다.
나는 지표의 분류를 다루는 것이 쓸모가 없다고 결론을 내립니다. 가격 상승과 관련이 없기 때문에 쓸모가 없습니다.
아니면 제가 틀렸나요?
...아니면 제가 틀렸나요?
맞는 것 같아요 :-)
faa1947님, 질문이 있습니다. 몇 가지를 명확히하고 싶었습니다... 제가 질문자님의 방정식에서 데이터를 계산한 방법은 다음과 같습니다:
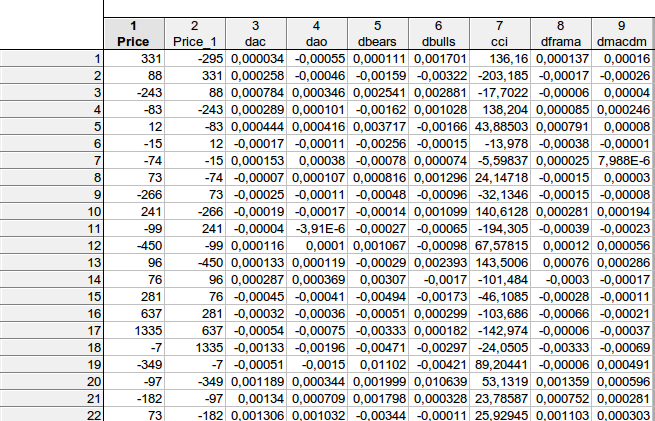
표의 데이터가 가격 가격(-1) DAC(-1) 다오(-1) 디비어스(-1) 디불스(-1) CCI(-1) 디프라마(-1) 디맥디엠(-1) 과 일치하나요?
그리고 다음과 같은 결과를 얻었습니다:
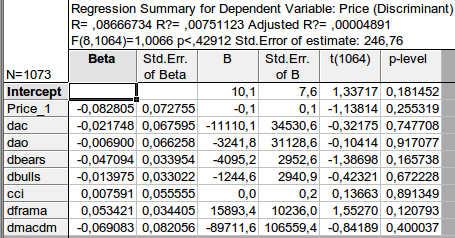
변수를 선택한 후에는 가격을 종속 변수(함수)로 하고 다른 지표를 독립 변수로 하는 관계를 만들어야 합니다. 다음은 개략적인 방정식입니다:
가격 가격(-1) DAC(-1) Dao(-1) DBARS(-1) DBULLS(-1) CCI(-1) DFAMA(-1) DMACDM(-1)
-1은 이전 값을 의미합니다. 이는 지표가 가격에서 분석적으로 파생되었기 때문에 자연스러운 현상입니다. 가격이 증분이라는 점을 고려하여 지표의 증분을 취하겠습니다. 게으름 때문에 모든 지표를 취하지는 않습니다. 이 방정식을 최소제곱법으로 추정해 보겠습니다:
방정식 계수의 추정치를 얻었습니다. 마지막 열은 매우 흥미롭습니다. 해당 계수가 0과 같을 확률을 의미합니다. 모든 계수에 대한 이 확률은 최소 10%보다 훨씬 높습니다. 즉, 해당 계수가 0이라는 가설을 거부할 수 없다는 것을 고려할 수 있습니다. 따라서 R- 제곱은 우스꽝스러운 값을 갖습니다.
나는 지표의 분류를 다루는 것이 쓸모가 없다고 결론을 내립니다. 가격 상승과 관련이 없기 때문에 쓸모가 없습니다.
아니면 제가 틀렸나요?
사용한 통계 방법의 이름을 알려주세요. 입력은 지표이고 출력은 미래 가격인 선형 회귀 방정식을 구성했다고 들었는데 맞나요? 맞나요? 외환은 선형 결정론적 시스템이 아니므로 이 방법은 작동하지 않습니다. 판별 분석은 시스템에 대한 외부 설명을 기반으로 패턴 인식을 위한 모델을 구축하는 다른 작업을 수행합니다.
가격 상승을 분석하기 위해 지표를 분류하는 것이 쓸모없다면 기술적 분석은 의미가 없을 것입니다. 다행히도 가격은 혼란스럽게 움직이지 않고 이전 이벤트에 대한 기억을 가지고 있습니다.
맞는 말씀인 것 같습니다 :-)
faa1947님, 질문이 있습니다. 몇 가지를 명확히 하고 싶어서요... 제가 질문자님의 방정식에서 데이터를 계산한 방법은 다음과 같습니다:
표의 데이터가 가격 가격(-1) DAC(-1) 다오(-1) 디비어스(-1) 디불스(-1) CCI(-1) 디프라마(-1) 디맥디엠(-1) 과 일치하나요?
그리고 다음과 같은 결과를 얻었습니다:
원시 데이터는 다음과 같습니다:
방정식은 다음과 같습니다:
추정 방정식
=========================
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
대체된 계수:
=========================
가격 = -0.0228102658125*가격(-1) + 12005.8974278* DAC(-1) + 4033.10946937*DAO(-1) + 3176.11232129*DBARS(-1) - 6021.36196728*DBULLS(-1) - 0.102710105369*CI(-1) - 11487.4273249*DFRAMA(-1) + 62535.3387412*DMACDM(-1)
계산이 이해가 되지 않습니다. 저는 지연 값(이전 값)을 사용하는 원칙을 가지고 있습니다. 이를 통해 예측을 할 수 있습니다. 지연 -1이 첫 번째 관측에 해당하면 종속 변수는 예측된 새로운 미관측 관측에 해당합니다.
P-레벨이란 무엇인가요? 저에게는 해당 계수가 0일 확률입니다.
사용한 통계 방법의 이름을 알려주세요. 입력은 지표이고 출력은 미래 가격인 선형 회귀 방정식인가요? 맞나요?
회귀식은 최소제곱법을 사용하여 추정했습니다. 예측을 하는 데 사용할 수 있습니다.
외환은 선형 결정론적 시스템이 아니므로 이 방법은 작동하지 않습니다.
선형이라면 특정 예시입니다. 계수조차도 무작위 변수로 취급되기 때문에 결정론적이지 않습니다. 모든 계수는 계산된 것이 아니라 추정치입니다. 두 번째 열은 계수 추정의 표준 오차를 보여줍니다. 매우 크다는 점에 유의하시기 바랍니다.
가격 상승을 분석하기 위한 지표 분류가 쓸모없다면 기술적 분석은 무의미할 것입니다.
바로 그렇고, 저만 그렇게 생각하는 것은 아니라고 감히 말씀드릴 수 있습니다. 기술적 분석은 과학이 아니라 점성술의 일종입니다. 원래 300년 전에는 코티르를 시각화하는 시스템이었죠. 그 이후로 엄청나게 발전했습니다. 다른 모든 것은 기적의 분야의 피노키오를위한 것입니다. 규칙적이고 반복 가능한 생각을 담고 있는 글이라 만족스러웠습니다.
가격 상승을 분석하기 위한 지표의 분류가 쓸모없는 경우
여기서 우리는 지표의 특별한 경우를 분석했습니다. 특정 지표나 그 사용이 시세와 관련이 있다는 것을 증명하는 것은 항상 필요합니다. TA는 이 문제를 고려하지 않습니다.
다행히도 가격은 혼란스럽게 움직이지 않고 이전 이벤트에 대한 기억을 가지고 있습니다.
모든 계량경제학은 시세에 결정적 요소(자기 상관관계, 메모리)와 잡음이 있다는 가정을 기반으로 합니다.
판별 분석은 시스템의 외부 설명을 기반으로 패턴 인식을 위한 모델을 구축하는 다른 작업을 수행합니다.
작업은 명확합니다. 그러나 얻은 결과를 신뢰할 수 있는지 여부가 문제입니다. 문제는 분류(이 또한 해결해야 할 문제의 일부임)가 아니라 결과 예측에 대한 신뢰입니다. 이것이 바로 문제입니다.
계산이 이해가 되지 않습니다. 제 원칙은 지연 값(이전 값)을 사용하는 것입니다. 이를 통해 예측을 할 수 있습니다. 지연 -1이 첫 번째 관측에 해당하면 종속 변수는 예측된 새로운 미관측 관측에 해당합니다.
P-레벨이란 무엇인가요? 저에게는 해당 계수가 0일 확률입니다.
faa1947, 나는 지연이있는 테이블을 제공했습니다 (처음 몇 행에 대해 - 전체 테이블을 맞출 수 없음). 그러나 먼저 지표 차이를 계산하여 총 행 수는 1074가 아닌 1073입니다. 그런 다음 종속 변수 Price를 한 단계 앞으로 이동했습니다.
첫 번째 줄의 예에서 다음과 같이 나타났습니다:
331 = C(1)*(-295) + C(2)* 0.000034 + C(3)* (-0.00055) + C(4)* 0.000111 + C(5)* 0.001701 + C(6)*136.16 + C(7)* 0.000137 + C(8)*0.00016, 즉 다음과 같이 계산됩니다.
가격 = C(1)*가격(-1) + C(2)* DAC(-1) + C(3)*DAO(-1) + C(4)*DBARS(-1) + C(5)*DBULLS(-1) + C(6)*CI(-1) + C(7)*DFAMA(-1) + C(8)*DMACDM(-1)
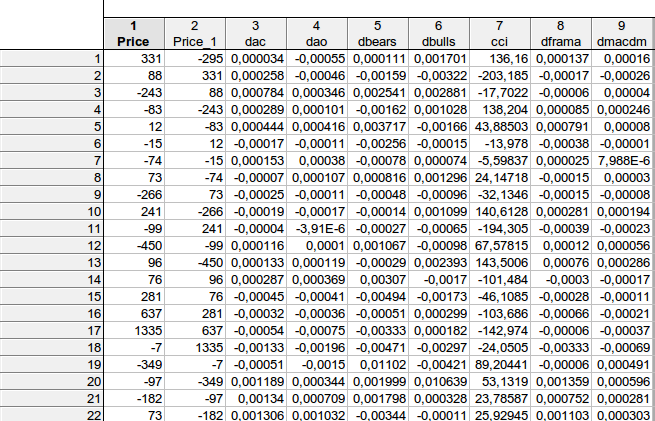
일반적으로 나는 대략 비슷한 결과를 얻었습니다. 고려 된 계수가 0과 같다는 귀무 가설을 거부 할 방법이 없습니다 ...
새로운 기고글 판별 분석을 이용한 매매 시스템 구축 가 게재되었습니다:
자동 매매 시스템을 만들다 보면 어떤 인디케이터와 어떤 신호가 가장 잘 맞을지 선택하기 어려울 때가 있습니다. 판별 분석은 인디케이터와 신호 간의 조합을 찾는 데에 도움이 되는 방법 중 하나인데요. 이 글은 시장 데이터 수집용 엑스퍼트 어드바이저 개발과 스타티스티카(Statistica)를 이용한 외환 시장(FOREX)용 예측 모델에 대한 판별 분석 적용법을 다룹니다.
관련 예제는 MasterData.CSV에 포함되어 있습니다. 2011년 8월 1일부터 2011년 10월 1일까지 EURUSD H1에 대한 데이터가 수집되었습니다.
다음의 설명을 따라 스타티스티카에서 파일을 여세요.
작성자: ArtemGaleev