記事"メリルパターン"についてのディスカッション

新しいコメント
 

新しい記事 メリルパターン はパブリッシュされました:

本稿では、メリルパターンのモデルを見て、それらの現在の関連性を評価します。これを行うために、パターンをテストし、終値、高値、安値、オシレータなどのさまざまなデータタイプにモデルを適用するツールを開発します。

メリルパターンをどのように、またどのデータに適用するのかを明確にするために、それらが実際に何であるかを理解する必要があります。主な2つのカテゴリは、文字MとWに似たパターンです。これらはMパターンとWパターンと呼ばれます。各カテゴリには16個のパターンが含まれています。

図1は16個のMパターンを表します。ご覧のように、違いはパターンを構成する5つの点の相互配置にあります。  

作者: Alexander Fedosov

 
写真のM2とM4のパターンは同じだが、これはタイプミスか？
 

興味深い資料、ありがとう！

私はパターン認識の実装が好きではなかった：

//+------------------------------------------------------------------+
//|| パターン認識|
//+------------------------------------------------------------------+
PATTERN_TYPE CProgram::GetPatternType(double A,double B,double C,double D,double E)

おそらくこの記事にとっては最適解なのだろう。


この問題に対するもっとエレガントな（普遍的な）解決策を見つけたいのですが、データ（配列）を格納するための行列のようなものでしょうか？- 誰かそのようなパターン 検索の実装に出会ったことはないだろうか？

 
Sergey Pavlov:
写真のM2とM4のパターンが同じですが、タイプミスでしょうか？

修正します。

 
Igor Makanu:

興味深い内容だ！

パターン認識の実装が気に入らなかった：

おそらくこの記事にとっては最適解なのだろう。


この問題に対するもっとエレガントな（普遍的な）解決策を見つけたいのだが、データ（配列）を格納するための行列のようなものだろうか？- パターン・サーチのそのような実装に出会った人はいるだろうか？

もちろん、すべてを構造体や配列に入れることもできる。しかし、今のところ、ポリラインの点の形でゼロから理解する方が簡単だ。

 
Igor Makanu:

...

この問題に対するもっとエレガントな（普遍的な）解決策を見つけたいのですが、データ（配列）を格納するための行列のようなものはないでしょうか？- 誰かそのようなパターン・サーチの実装に出会ったことがありますか？

私は普遍的にやったことがある。でも、見つけられそうにない。どこから探し始めたらいいのかさえわからない。

1本の線があり、2つの点がある。3つ目の点は、1つ目の点と2つ目の点の間か、1つ目の点の上（1つ目の線が上向きだとする）の2つの位置のどちらかを占めることができる。今3つの点があり、4番目の点は3つの位置のうちの1つ、または2つの位置のうちの一番下を占めることができる。まず配列に2つの点があり、インデックス1に立ち、3番目の点の位置のすべての変種を配列の最後に加える。インデックス2に移動し、別の点のすべての変種を配列の末尾に追加する....など。配列のサイズが 指定されたサイズに達すると同時に、パターン自体が数字で設定される。構造体の配列が必要で、構造体の中に点番号を持つ配列が必要である。

***

配列には点の座標ではなく、最初から頂点の番号が入る。例えば、M16はこのようにエンコードされる：{1, 3, 2, 5, 4}.さらに頂点を追加すると、次のようになります。

{1, 3, 2, 5, 4}

{1, 3, 2, 5, 6, 4}

{1, 3, 2, 5, 4, 6}


***

これをチェックする方法はこうだ。例えば、{1, 3, 2, 5, 4} というパターンを探すとします。 これは頂点1が3より下にあり、5が2より上で4より下にあることを意味します。

 
Dmitry Fedoseev:

それは普遍的なものだった。でも、それを見つけられるとは思えないし、何から探せばいいのかもわからない。

1本の線があり、それは2つの点である。3つ目の点は、1つ目の点と2つ目の点の間、または1つ目の点の上（1つ目の線が上向きだと仮定する）の2つの位置のいずれかを占めることができる。さて、3つの点があり、4つ目の点は3つの位置のうちの1つ、または2つの位置のうちの一番下を占めることができる...。まず配列に2つの点があり、インデックス1に立ち、3番目の点の位置のすべての変種を配列の最後に加える。インデックス2に移動し、別の点のすべての変種を配列の末尾に追加する....など。配列のサイズが指定されたサイズに達すると同時に、パターン自体が数字で設定される。構造体の配列が必要で、その中に点番号を持つ配列がある。

***

配列には点の座標ではなく、最初から頂点の番号が入る。例えば、M16はこのようにエンコードされる：{1, 3, 2, 5, 4}.さらに頂点を追加すると、以下のようになります。

{1, 3, 2, 5, 4}

{1, 3, 2, 5, 6, 4}

{1, 3, 2, 5, 4, 6}


***

それをチェックする方法はこうだ。例えば、{1, 3, 2, 5, 4} というパターンを探すとしよう。これは、頂点1が3より下にあり、5が2より上で4より下にある、といった意味だ。

ああ、僕が見つけたいのはそういうコーディングだ。

重み付けされたグラフの隣接行列の ようで、重みはどの頂点が現在の頂点より上か下かを意味する。

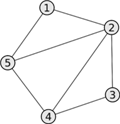
Матрица смежности графа — Викиконспекты
Матрица смежности графа — Викиконспекты
  • neerc.ifmo.ru
Матрицей смежности (англ. Adjacency matrix) невзвешенного графа называется матрица , в которой — количество рёбер, соединяющих вершины и , причём при каждую петлю учитываем дважды, если граф не является ориентированным, и один раз, если граф ориентирован. Матрицей смежности (англ. Adjacency matrix) взвешенного графа называется матрица , в...
 

問題提起とそのソフトウェア的解決策、そしてグラフィカル・インターフェースの実装の両面で、素晴らしい仕事ぶりだ。

可能であれば、市場参入 点を見つけるための数値自体の有効性に関する研究結果も加えてほしい。

おそらく、この課題は膨大であるため、別のトピックと別の出版物にすることができるだろう。

 
Aleksandr Masterskikh:

問題提起とそのソフトウェア・ソリューション、そしてGUIの実装の両面で、素晴らしい仕事だ。

可能であれば、市場のエントリー・ ポイントを見つけるための数値そのものの有効性に関する調査結果も加えてほしい。

おそらく、この課題は膨大であるため、別のトピックとし、別の出版物とすることができるだろう。

アレクサンダー、私の記事を気に入ってくれてありがとう。調査については、この記事のアプリケーションは準備ができている。現在のカスタマイズ・オプションは、すでに検索に関する多くのオプションを提示している。

次の記事では、アプリケーションの可能性を広げてみようと思います。

 
Alexander Fedosov:

もちろん、すべてを構造体や配列にすることもできる。しかし、こうしてポリラインの点という形でゼロから理解する方が簡単だ。

普遍性に加えて、記事のコードが明快で読みやすいものであるべきなのは明らかだが、私は組み合わせ問題や頭をくねらせるのが好きなので、MEで検索してこの関数を最初の条件でグループ化した：

//+------------------------------------------------------------------+
//|| パターン認識|
//+------------------------------------------------------------------+
PATTERN_TYPE GetPatternType(double A,double B,double C,double D,double E)
  {
   if(A>B && C>A && B>E && E>D) return(W6);
   if(A>B && C>E && E>A && B>D) return(W11);
   if(A>B && E>C && C>A && B>D)return(W12);
   if(A>B && C>E && E>D && D>A)return(W15);
   if(A>B && E>C && C>D && D>A) return(W16);

// A>C
   if(A>C && B>D && D>A && C>E) return(M3);
   if(A>C && B>D && D>E && E>A) return(M8);
   if(A>C && D>B && B>E && E>A) return(M10);
   if(A>C && C>B && B>E && E>D) return(W1);
   if(A>C && C>E && E>B && B>D) return(W2);
   if(A>C && C>E && E>D && D>B) return(W4);
   if(A>C && E>A && C>B && B>D) return(W8);
   if(A>C && E>A &&  C>D && D>B)return(W10);
// C>A else ? 
   if(C>A && B>D && D>C && A>E) return(M7);
   if(C>A && D>B && B>C && A>E) return(M9);
   if(C>A && B>D && D>E && E>C) return(M13);
   if(C>A && D>B && B>E && E>C) return(M15);
   if(C>A && D>E && E>B && B>C) return(M16);
   if(C>A && A>E && E>B && B>D) return(W7);
   if(C>A && A>E && E>D && D>B) return(W9);
   if(C>A && E>C && A>D && D>B) return(W14);
   
   
   if(B>A && A>D && D>C && C>E) return(M1);
   if(B>A && A>D && D>E && E>C) return(M2);
   if(B>A && D>B && A>C && C>E) return(M5);
   if(B>A && D>B && A>E && E>C) return(M6);
   if(B>A && D>E && E>B && A>C) return(M11);
   

   if(B>D && D>A && A>E && E>C) return(M4);
   if(B>D && D>C && C>E && E>A) return(M12);
   if(B>D && A>E && E>C && C>B) return(W3);
   if(D>B && B>C && C>E && E>A) return(M14);
   if(D>B && A>E && E>C && C>D) return(W5);
   if(D>B && C>E && E>A && A>D) return(W13);
   
   
   return(-1);
  }

コンパクトで普遍的な解がまだあるはずなのだが......。しかし、私はまだそれを見ていない

 
Igor Makanu:

普遍性に加えて、記事のコードも視覚的で読みやすいものであるべきなのは明らかだが、私は組み合わせ論に関する問題や、頭をくねらせるのが好きなので、この関数をMEで検索して最初の条件でグループ化した：

まだコンパクトで普遍的な解があるはずなのだが......。しかし、私はまだそれを見ていない

そこでドミトリーが提案してくれたのが、上記の良い解決策だ。この方法で再生することができます：

GetPatternTypeメソッドの引数にパターンの次元を渡す。GetPatternTypeメソッドの引数でパターン次元を渡すと、それだけでこの数値からすべての可能な組み合わせを作成し、このデータに基づいて構造体または配列から指定されたものを検索します。

12
新しいコメント