Discussione sull’articolo "Combinatoria e teoria della probabilità per il trading (Parte II): Frattale universale"
Se è possibile, chiedo all'autore di questo articolo di considerare i seguenti argomenti:
Finora ho visto che il principio del rapporto aureo può essere usato per costruire catene frattali-probabilistiche che formano un gruppo completo di eventi, ma onestamente non vedo cosa possa dare un tale approccio. Sembra che il rapporto aureo sia anche collegato alla serie di fibo, ma anche in questo caso non vedo come possa essere applicato e per cosa, se avete idee da scrivere qui, penso che sarà un vantaggio. E quindi in generale questi processi si sono già formati nella mia testa, in generale è tutto ciò che serve per ricavare formule più complesse. Finora i frattali ottenuti svolgono il loro compito. Tutto passa dal complesso al semplice e così via. Posso pensare all'applicazione del rapporto aureo, ma non vedo come possa essere utile. Anche le serie di fibo, tutti dicono fibo-fibo... Ololo, sentono una parola intelligente e la ripetono come un pappagallo. Io procedo sempre dal fatto che un principio matematico corrisponde a un problema particolare, e trovo sempre una soluzione a qualsiasi problema dopo qualche tempo. Lo strumento della soluzione viene selezionato nel processo, il cervello stesso lo trova e, se possibile, trova delle somiglianze con qualcosa che è all'orecchio. In altre parole, prima determiniamo ciò che dobbiamo trovare e poi cerchiamo i modi per risolvere il problema. Sarei più interessato a sentire problemi specifici, e si può fare un articolo separato con tali soluzioni, sarebbe interessante e divertente, credo. Nell'ambito di questi problemi possiamo applicare il rapporto aureo e qualsiasi altra cosa, purché il risultato sia davvero necessario e dia un beneficio concreto a qualcuno. Quindi potete scrivere suggerimenti.
Se è possibile, chiedo all'autore di questo articolo di considerare i seguenti argomenti:
Questo è solo un mito trito e ritrito di presunti fibo e ZS ovunque....
La cosa divertente è che se si prende una pentola qualsiasi e la si rigira bene, vi si possono trovare sia fibo che il rapporto aureo e pi greco e molte altre cose....
È solo un mito trito e ritrito quello del fibo e dello ZS ovunque e dappertutto...
La cosa divertente è che se si prende una pentola qualsiasi e la si fa girare bene, vi si può trovare il fibo e il rapporto aureo e il numero di pi greco e il numero di e e molte altre cose....
La fiba (che è anche il rapporto aureo, cosa di cui molti non si rendono conto) si cerca, cioè si vede, con estrema facilità. Perché sono esponenziali. Che a loro volta sono somme... In generale, si può parlare a lungo di cose elementari della scuola (!!!), ma è inutile.
Si può anche fare così:
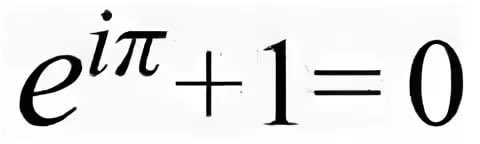
bello, misterioso... la connessione di FIBO con Fourier... le costanti del mondo in un bicchiere... e altre cose.
È solo un mito trito e ritrito quello del fibo e dello ZS ovunque e dappertutto...
La cosa divertente è che se si prende una pentola qualsiasi e la si fa girare bene, vi si può trovare il fibo e il rapporto aureo e il numero di pi greco e il numero di e e molte altre cose....
Se lo mettete in testa, potete anche trovarci la testa e le spalle).
È solo un mito trito e ritrito che Fibo e ZS siano ovunque e ovunque....
La cosa divertente è che se si prende una pentola qualsiasi e la si rigira bene ci si può trovare dentro fibo e rapporto aureo e pi greco e e molte altre cose....
Non potrei essere più d'accordo )) è proprio vero. Ai trader piace molto cercare un significato nascosto dove non ce n'è affatto). Sto cercando di trasmettere con attenzione la stessa cosa alle persone, ma non so come farlo senza dire la verità, e la verità è crudele ). Sono arrivato al punto che c'è un problema e c'è un insieme di possibili soluzioni, e tutto ciò che non è così è una perdita di tempo. Per arrivare a una soluzione, bisogna prima impostare chiaramente il problema e avere almeno un'idea superficiale delle possibili vie di soluzione, se non ci sono tali vie, allora inizia quello che c'era sopra, Fibonacci, le formule di Eulero e altre stupidaggini molto belle ma talmente inutili che si comincia involontariamente a leggere tra le righe. Ogni strumento ha il suo compito. A questo proposito, propongo di entrare nello specifico (compiti specifici).
Finora ho visto che il principio del rapporto aureo può essere usato per costruire catene di probabilità frattali che formano un gruppo completo di eventi, ma onestamente non vedo cosa possa fare questo approccio. Sembra che il rapporto aureo sia anche collegato alle serie di fibo, ma anche in questo caso non vedo come possa essere applicato e per cosa, se avete idee da scrivere qui, penso che sarà un vantaggio. In generale questi processi si sono già formati nella mia testa, in generale è tutto ciò che serve per ricavare formule più complesse. Finora i frattali ottenuti svolgono il loro compito. Tutto passa dal complesso al semplice e così via. Posso pensare all'applicazione del rapporto aureo, ma non vedo come possa essere utile. Anche le serie di fibo, tutti dicono fibo-fibo... Ololo, sentono una parola intelligente e la ripetono come un pappagallo. Io procedo sempre dal fatto che un principio matematico corrisponde a un problema particolare, e trovo sempre una soluzione a qualsiasi problema dopo qualche tempo. Lo strumento della soluzione viene selezionato nel processo, il cervello stesso lo trova e, se possibile, trova delle somiglianze con qualcosa che è all'orecchio. In altre parole, prima determiniamo ciò che dobbiamo trovare e poi cerchiamo i modi per risolvere il problema. Sarei più interessato a sentire problemi specifici, e si può fare un articolo separato con tali soluzioni, sarebbe interessante e divertente, credo. Nell'ambito di questi problemi possiamo applicare il rapporto aureo e qualsiasi altra cosa, purché il risultato sia davvero necessario e dia un beneficio concreto a qualcuno. Quindi potete scrivere dei suggerimenti.
1. Forse tutti hanno sentito parlare di questo "ololo", ma io non ho scritto di fibo, perché non consiglio di "tirare" i livelli di fibo, anche se se sono calcolati correttamente, possono essere utilizzati, ma in combinazione con le onde di Elliott.
Naturalmente, questo non è tutto, vi rendete conto di quanto sia lungo e minuzioso questo lavoro, ma ho iniziato questo thread per un motivo. Cercherò di fare tutto ciò che dipende da me, e in generale tali questioni, ad essere onesti, dovrebbero essere affrontate da un intero team di matematici e programmatori, se non da un intero istituto. Cosa può fare una sola persona contro di essa? Anche se si ha un super cervello, ci sono così tanti dati da elaborare che si può impazzire. Sto cercando di stabilire i compiti che sono commisurati al mio tempo e alle mie capacità; sì, posso fare di più, ma ora non dipende da me. Il tempo è la risorsa più preziosa. Se ci fossero persone interessate ad analisi complesse e a una dedizione completa, sarei felice di farlo. Tuttavia, il ramo continuerà e coprirò il materiale che posso, cercando sempre di raccontare qualcosa di nuovo, per quanto possibile.
Il mito dell'universalità del rapporto aureo in natura è cresciuto a tal punto che la gente non si preoccupa nemmeno di fare verifiche reali, cedendo al fascino della bellezza dell'idea stessa del rapporto tra il tutto e le sue parti, ma in realtà non è così:
- le conchiglie dei molluschi-nautilus (che di solito vengono illustrate negli articoli sulla magia del WD) contrariamente all'opinione popolare non corrispondono al WD.
- Le proporzioni di un corpo umano tratte dal famoso disegno di Leonardo Da Vinci "Uomo Vitruviano" non sono osservate in relazione alle persone reali.
- Partenone, Piramidi e altri oggetti corrispondono in modo molto impreciso a RS (disegnati dagli amanti del misticismo).
- Le ricerche psicologiche oggettive con lo scopo di rivelare se l'EQ è alla base della percezione della bellezza sono fallite con successo.
- Infine, anche i test quantitativi di rottura/rifiuto dei livelli nel trading non dimostrano che l'EQ sia qualcosa di particolarmente importante.
L'unica ragione per cui i mercati possono a volte (parola chiave UN'ALTRA VOLTA) effettuare piacevoli pullback/breakout dei livelli di fibo è la convinzione collettiva di un gran numero di trader tecnici sui livelli di fibo (una profezia che si autoavvera) se collettivamente vi pongono i loro stop/limiti, ma anche questo probabilmente non funzionerà perché i partecipanti professionali, i grandi operatori istituzionali faranno trading su altre basi, e la rottura/inversione del livello di Fibo potrebbe essere solo casuale, ma per i credenti nel QE sarà certamente una conferma della loro fede.
Keith Devlin, professore di matematica all'Università di Stanford, lo spiega semplicemente: "..... La maggior parte delle persone non capisce la matematica e non riesce nemmeno a capire come una formula come quella del rapporto aureo si applichi a un sistema complesso, quindi non può nemmeno fare un test. Le persone pensano di vedere il rapporto aureo ovunque, in natura e nei loro oggetti preferiti, ma non possono dimostrarlo. Sono vittime del loro naturale desiderio di trovare un significato nei vari oggetti dell'universo, ma a causa della loro mancanza di conoscenze matematiche non riescono a rendersi conto che i modelli che individuano sono illusori".
Le persone si programmano (zombie) per cercare una spiegazione semplice e si sforzano di mantenere questa convinzione, questa è l'essenza del pensiero religioso, anche nel commercio...
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Il nuovo articolo Combinatoria e teoria della probabilità per il trading (Parte II): Frattale universale è stato pubblicato:
In questo articolo continueremo a studiare i frattali e presteremo particolare attenzione a riassumere tutto il materiale. A tal fine, cercherò di riunire tutti gli sviluppi precedenti in una forma compatta che sia comoda e comprensibile per l'applicazione pratica nel trading.
Utilizziamo le regole di costruzione derivate nell'articolo precedente e integriamole per capire come si costruisce un frattale. Inoltre, ho trovato un piccolo errore nelle mie formule, a causa del quale l'asimmetria dei bordi verso il basso o verso l'alto era impossibile. Le formule derivate si sono rivelate corrette e quindi funzionano per qualsiasi frattale. In realtà, si tratta di una funzione per implementare qualsiasi frattale. Tutti i frattali possibili sono un caso speciale di un frattale generale. Se prendiamo i tre tipi di frattali definiti sopra, le condizioni del frattale generale per l'implementazione di questi tre casi speciali saranno le seguenti:
Schematicamente, questi tre tipi di frattali si presentano come segue:
Idealmente, "S" dovrebbe tendere all'infinito. Le seguenti variabili non sono state descritte nel mio precedente articolo. Fornirò qui le descrizioni pertinenti per avere un quadro completo di come utilizzare la formula generale per ottenere i casi speciali. Un frattale è una funzione che funziona secondo il principio della reazione a catena, come in una bomba atomica. Se la reazione a catena impostata è troppo profonda, il computer potrebbe non riuscire a gestire calcoli così massicci. Se il caso non è particolarmente critico, si tratterà semplicemente di un tempo molto lungo — minuti, ore o addirittura giorni.
Autore: Evgeniy Ilin