Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
È ovvio che si dovrebbe ritirare q e solo alla fine del periodo t. In tutti gli altri casi l'importo ritirato sarà inferiore a
Il riccio ha deciso di usare i calcoli analitici))))
Il problema non ha estremi, perché abbiamo una serie numerica monotonicamente crescente - una funzione con un argomento nella forma della dimensione del deposito. Cioè non c'è niente da ottimizzare. Maggiore è l'argomento e t, maggiore è il valore della funzione. In ogni altro caso il valore della funzione diminuirà.
È difficile cercare un gatto nero in una stanza buia, soprattutto se non è lì (c) Confucio
Non resta che prendere la derivata del tempo ed equipararla a zero... Sì...
A proposito, semmai la derivata dovrebbe essere presa su k
Pardon! Davvero sulla k .
Reshetov:
È ovvio che dovete ritirare q e solo alla fine del periodo t. In tutti gli altri casi l'importo prelevato sarà inferiore.
Yura, sei così sicuro di te che è divertente quando ti sbagli.
Nella prima pagina, avtomat ha dato un'immagine dove si vede chiaramente l'optimum sul parametro k . Forse non te ne sei accorto. Ve ne mostrerò un altro:
Vedete il massimo? No? Ma è lì!
Riposati, riccio.
Impossibile!...
Puoi essere più specifico? Cioè, sotto forma di formula.
In altre parole, l'optimum in termini di percentuale di prelievo è davvero visibile!
Recentemente ho risolto un problema simile...
E poi combiniamo tutto questo insieme e otteniamo la funzione risultante di due variabili.
Va anche detto che il risultato dipende dal periodo di ottimizzazione, cioè
l'optimum per 12 mesi non è uguale a quattro optimum per periodi di 3 mesi.
Recentemente ho risolto un problema simile...
Esatto, avtomat. È esattamente così che si comporta. Ma ho davvero bisogno di ottenere una soluzione analitica per la frazione ottimale di k. Se si prende la derivata di k da f(k), si ottiene la seguente equazione: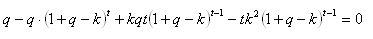
La figura qui sotto mostra chiaramente che l'ascissa dove df/dk è zero coincide con il massimo di f(k).
Ma come risolverlo rispetto a k?
Beh, il problema non ha niente a che fare con il trading comunque. È un problema di rentier. Sarebbe abbastanza appropriato per quel ramo.
P.S. Mi chiedo, cosa farà Jura in questa situazione? Farà finta di non aver notato nulla (nessun massimo sul parametro k ) e non lascerà commenti sull'argomento o dovrà riconsiderare le sue ipotesi di base per la vita...
P.S. Mi chiedo cosa farà Jura in questa situazione? Farà finta di non accorgersi di nulla (nessun massimo per il parametro k ) e non lascerà più commenti sull'argomento, o dovrà rivedere i suoi principali set point a vita...
Mi è stato permesso di utilizzare un deposito di X0 rubli per t mesi. Ogni mese il deposito viene accreditato con una percentuale fissa q dell'importo corrente del deposito X. Sono autorizzato a ritirare ogni mese una certa percentuale k dal conto che non supera il valore di q.
Ho il permesso di aprire operazioni con la dimensione del lotto HO. Ogni trade positivo aperto ha un u% di possibilità di accumulare w pips, guadagnando q ovviamente dal valore corrente del deposito XO. Ho il permesso di chiudere parzialmente un ordine di una certa percentuale k tutte le volte che voglio (fino al 100% di chiusura) con una frequenza di n pips che non supera w.
Domanda: trovare rispetto a u%, valori ottimali di k, n.
Esatto, avtomat. È esattamente così che si comporta. Ma ho davvero bisogno di ottenere una soluzione analitica per la frazione ottimale di rimozione k. Se si prende la derivata di k da f(k), si ottiene la seguente equazione:
La figura qui sotto mostra chiaramente che l'ascissa dove df/dk è zero coincide con il massimo di f(k).
Ma come risolverlo rispetto a k?
se l'equazione di cui sopra è vera, allora possiamo farlo:
Ma di nuovo, quali sono i requisiti, quali sono le condizioni...
q e t -- date quantità costanti o ...