Discussione sull’articolo "Utilizzo dell'analisi discriminante per sviluppare sistemi di trading"
All'autore (senza nickname per qualche motivo).
Lo stesso problema può essere risolto in altri modi. Esistono test per le variabili ridondanti e mancanti. Potrei farlo e confrontarlo con i vostri risultati. Ma ho bisogno di tutti i vostri file in formato .csv.
...Ho bisogno di tutti i file in formato .csv.
Credo che l'origine sia nell'archivio masterdata.zip.
Articolo pubblicato Utilizzo dell'analisi discriminante per costruire sistemi di trading:
Autore: ArtemGaleev
Dopo aver scelto le variabili, dovremo creare una relazione tra di esse, in cui il prezzo sarà la variabile dipendente (funzione) e gli altri indicatori saranno le variabili indipendenti. Ecco l'equazione schematica:
prezzo prezzo(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 significa il valore precedente. Ciò è naturale poiché l'indicatore è derivato dal prezzo in modo analitico. Teniamo conto del fatto che il prezzo è un incremento, quindi prenderemo gli incrementi degli indicatori. Per pigrizia, non prendo tutti gli indicatori. Stimiamo questa equazione con il metodo dei minimi quadrati:
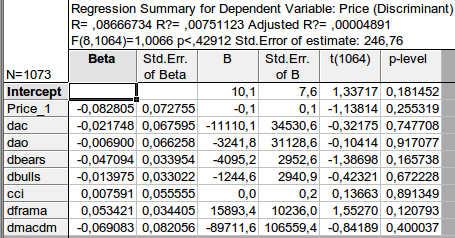
Abbiamo ottenuto una stima dei coefficienti dell'equazione. L'ultima colonna è molto interessante: indica la probabilità che il coefficiente corrispondente sia uguale a zero. Questa probabilità per tutti i coefficienti è molto più alta di almeno il 10%, cioè possiamo ritenere di non poter rifiutare l'ipotesi che i coefficienti corrispondenti siano uguali a zero. Di conseguenza, il coefficiente R ha un valore ridicolo.
Concludo che è inutile occuparsi della classificazione degli indicatori: sono inutili perché non hanno nulla a che fare con l'incremento dei prezzi.
O mi sbaglio?
...O mi sbaglio?
Penso che tu abbia ragione :-)
faa1947, ho una domanda da farti. Volevo chiarire un paio di cose... ecco come ho calcolato i dati della tua equazione:
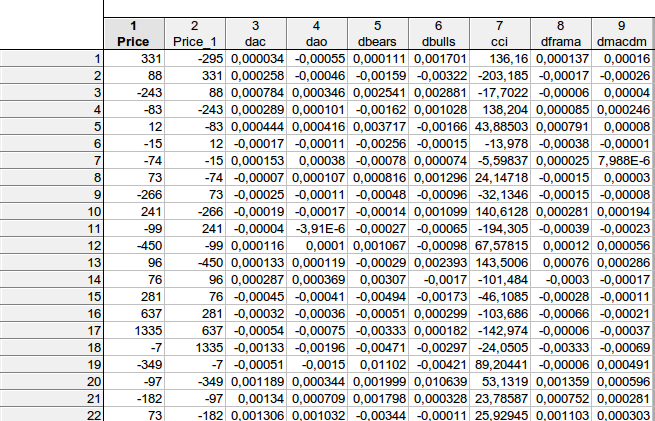
I dati della tabella corrispondono alla tua equazione schematica prezzo prezzo(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
E ho ottenuto il seguente risultato:
Una volta scelte le variabili, dovremo creare una relazione tra di esse, in cui il prezzo sarà la variabile dipendente (funzione) e gli altri indicatori saranno le variabili indipendenti. Ecco un'equazione schematica:
prezzo prezzo(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 indica il valore precedente. Ciò è naturale poiché l'indicatore è derivato dal prezzo in modo analitico. Teniamo conto del fatto che il prezzo è un incremento, quindi prenderemo gli incrementi degli indicatori. Per pigrizia, non prendo tutti gli indicatori. Stimiamo questa equazione con il metodo dei minimi quadrati:
Abbiamo ottenuto una stima dei coefficienti dell'equazione. L'ultima colonna è molto interessante: indica la probabilità che il coefficiente corrispondente sia uguale a zero. Questa probabilità per tutti i coefficienti è molto più alta di almeno il 10%, cioè possiamo ritenere di non poter rifiutare l'ipotesi che i coefficienti corrispondenti siano uguali a zero. Di conseguenza, il coefficiente R ha un valore ridicolo.
Concludo che è inutile occuparsi della classificazione degli indicatori: sono inutili perché non hanno nulla a che fare con l'incremento dei prezzi.
Oppure mi sbaglio?
La prego di fornire il nome del metodo statistico che ha utilizzato. Si tratta della costruzione di un'equazione di regressione lineare, in cui l'input sono gli indicatori e l'output è il prezzo futuro? È corretto? Questo non funziona per il forex, poiché non è un sistema deterministico lineare. L'analisi discriminante ha un compito diverso: costruisce modelli per il riconoscimento di pattern basati su descrizioni esterne del sistema.
Se classificare gli indicatori per analizzare gli incrementi di prezzo fosse inutile, l'analisi tecnica non avrebbe senso. Fortunatamente, il prezzo non si comporta in modo caotico, ma ha una memoria degli eventi precedenti.
Sembra che tu abbia ragione :-)
faa1947, ho una domanda da farti. Volevo chiarire un paio di cose... ecco come ho calcolato i dati della tua equazione:
I dati della tabella corrispondono alla tua equazione schematica prezzo prezzo(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
E ho ottenuto il seguente risultato:
I dati grezzi appaiono come segue:
Le equazioni appaiono come segue:
Equazione di stima:
=========================
PREZZO = C(1)*PREZZO(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DABORDI(-1) + C(5)*DBULLI(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
Coefficienti sostituiti:
=========================
PREZZO = -0.0228102658125*PREZZO(-1) + 12005.8974278*DAC(-1) + 4033.10946937*DAO(-1) + 3176.11232129*DBEARS(-1) - 6021.36196728*DBULLS(-1) - 0.102710105369*CCI(-1) - 11487.4273249*DFRAMA(-1) + 62535.3387412*DMACDM(-1)
Non capisco il tuo calcolo. Il mio principio è quello di utilizzare il valore di ritardo (valore precedente). In questo modo è possibile fare una previsione. Se il lag -1 corrisponde alla prima osservazione, la variabile dipendente corrisponde a una nuova osservazione non osservata e prevista.
Che cos'è il livello p? Per me è la probabilità che il coefficiente corrispondente sia zero.
Indicare il nome del metodo statistico utilizzato. Si tratta di un'equazione di regressione lineare in cui l'input è costituito dagli indicatori e l'output è il prezzo futuro? È corretto?
La regressione è stata stimata con il metodo dei minimi quadrati. Può essere utilizzato per fare previsioni.
Non funziona per il forex, poiché non è un sistema deterministico lineare.
Se è lineare, lo è in un esempio specifico. Non è deterministico perché anche i coefficienti sono trattati come variabili casuali. Tutti i coefficienti non sono calcolati, ma stimati. La seconda colonna mostra l'errore standard della stima dei coefficienti, che è enorme.
Se la classificazione degli indicatori per l'analisi degli incrementi di prezzo fosse inutile, l'analisi tecnica non avrebbe senso.
Esattamente, e vi assicuro che non sono l'unico a pensarla così. L'AT non è una scienza, ma un tipo di astrologia. In origine, 300 anni fa, era un sistema per visualizzare il kotir. Da allora si è evoluta enormemente. Tutto il resto è per i Pinocchi nel campo dei miracoli. Il suo articolo mi ha soddisfatto, perché presenta un pensiero regolare e ripetibile.
Se la classificazione degli indicatori per l'analisi dell'incremento dei prezzi era inutile
Qui abbiamo analizzato un caso particolare di indicatori. È sempre necessario dimostrare che un particolare indicatore o il suo utilizzo hanno a che fare con una quotazione. L'AT non prende mai in considerazione questo aspetto.
Fortunatamente, il prezzo non si comporta in modo caotico, ma ha una memoria degli eventi precedenti.
Tutta l'econometria si basa sul presupposto che una quotazione abbia una componente deterministica (autocorrelazione, memoria) e un rumore.
L'analisi discriminante ha un compito diverso, costruisce modelli per il riconoscimento di pattern basati su descrizioni esterne del sistema.
Il compito è chiaro. Ma se il risultato ottenuto possa essere attendibile, questo è il problema. Il problema non è la classificazione (che è una parte del problema, anch'essa da risolvere), ma la fiducia nella predizione risultante. È proprio questo il problema.
Non capisco il tuo calcolo. Il mio principio è quello di utilizzare il valore di ritardo (valore precedente). In questo modo è possibile fare una previsione. Se il lag -1 corrisponde alla prima osservazione, la variabile dipendente corrisponde a una nuova osservazione non osservata e prevista.
Che cos'è il livello p? Per me è la probabilità che il coefficiente corrispondente sia zero.
faa1947, ho fornito la tabella con i lag (per le prime righe - non posso inserire l'intera tabella). Ma prima ho calcolato le differenze degli indicatori, quindi il numero totale di righe è 1073 invece di 1074. Poi ho spostato la variabile dipendente Price un passo avanti.
È risultato che, sull'esempio della prima riga:
331 = C(1)*(-295) + C(2)* 0,000034+ C(3)* (-0,00055) + C(4)* 0,000111 + C(5)* 0,001701+ C(6)*136,16+ C(7)* 0,000137+ C(8)*0,00016, a condizione che
PREZZO = C(1)*PREZZO(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
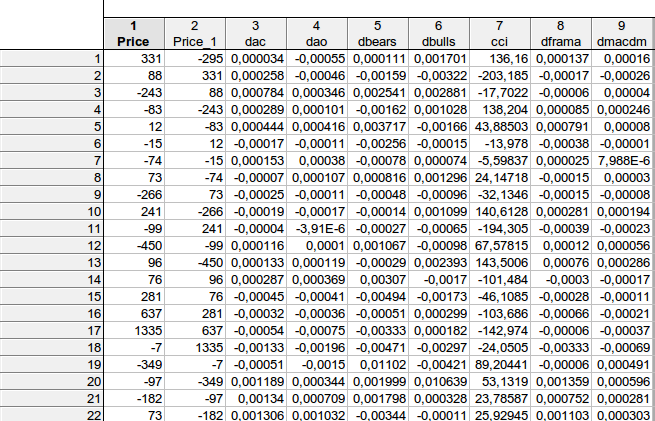
In generale, ho ottenuto un risultato simile - non c'è modo di rifiutare l' ipotesi nulla che i coefficienti considerati siano uguali a zero...
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Il nuovo articolo Utilizzo dell'analisi discriminante per sviluppare sistemi di trading è stato pubblicato:
Quando si sviluppa un sistema di trading, di solito si pone il problema di selezionare la migliore combinazione di indicatori e dei loro segnali. L'analisi discriminante è uno dei metodi per trovare tali combinazioni. L'articolo fornisce un esempio di sviluppo di un EA per la raccolta dei dati di mercato e illustra l'uso dell'analisi discriminante per la costruzione di modelli prognostici per il mercato FOREX nel software Statistica.
Il modello prognostico in DA si basa sul sistema di equazioni lineari secondo cui i valori degli indicatori sono classificati in un gruppo o nell'altro.
Per vedere le descrizioni di queste funzioni, vai alla scheda Classification nella finestra dei risultati DA (Figura 13) e clicca su Classification functions. Vedrai una finestra con una tabella contenente i coefficienti delle equazioni discriminanti.
Autore: ArtemGaleev