J'ai besoin d'interpoler une fonction avec des paramètres arbitraires, j'ai donc choisi les splines.
J'ai bien compris que j'obtiendrai des interpolants différents selon le nombre de points de nœud, que puis-je faire varier d'autre ?
Et la deuxième question, qu'est-ce qu'il vaut mieux choisir pour l'interpolation dans la liste, si j'ai juste besoin de construire de nombreuses interpolations différentes de la série originale (la variation est importante).
Le choix de la meilleure solution est une question très délicate. Une approche, appelée minimisation empirique du risque, est développée dans le livre de Wapnick intitulé Algorithms and Dependency Recovery Programs. 1972, semble-t-il.
La question de savoir quel est le meilleur choix est très délicate. Une approche, appelée minimisation du risque empirique, est développée dans le livre de Wapnick "Algorithms and programs for dependence reconstruction". Il semble que ce soit en 1972.
La maximisation/minimisation de la vraisemblance du risque empirique, telle que je la comprends, n'est qu'un nom général pour les algorithmes correspondants. Je n'ai pas besoin de l'algorithme lui-même, j'ai juste besoin de modifier des courbes, de préférence rapidement et de manière variable, avec la possibilité de trouver des valeurs interpolantes sur de nouveaux points (le package spline permet cette dernière possibilité).
La maximisation/minimisation de la vraisemblance du risque empirique, telle que je la comprends, n'est qu'un nom général pour les algorithmes correspondants. Je n'ai pas besoin de l'algorithme lui-même, j'ai juste besoin de modifier des courbes, de préférence rapidement et de manière variable, avec la possibilité de trouver des valeurs interpolantes sur de nouveaux points (le paquet spline permet cette dernière possibilité).
La méthode du maximum de vraisemblance et la minimisation (je me souviens, pas empirique, mais moyenne) du risque ne sont pas des noms d'algorithmes, mais des façons de fixer des objectifs dans la définition des problèmes. Si le but est réalisable, il donne lieu à un certain algorithme qui est nécessairement cohérent avec le but, est une mise en œuvre de sa réalisation dans des cas particuliers. Si vous n'avez besoin ni d'objectifs ni d'algorithmes pour les atteindre, aucun conseil ne peut être donné pour le choix des fonctions d'interpolation. Il vous reste à choisir ce que votre cœur vous dit...
Je dois interpoler une fonction avec des paramètres arbitraires, j'ai donc choisi les splines.
J'ai bien compris que j'obtiendrai des interpolants différents selon le nombre de points de nœud, que puis-je faire varier d'autre ?
Et la deuxième question, que dois-je sélectionner pour l'interpolation dans la liste, si j'ai seulement besoin de construire de nombreuses interpolations différentes de la série initiale (la variabilité est importante) ?
Le plus précieux pour un trader n'est pas l'interpolation ni l'approximation, mais l'extrapolation.
Les splines ne conviennent pas à l'extrapolation.
J'ai une grande expérience et compréhension de l'approximation-extrapolation polynomiale. Fourier est moins expérimenté.
L'extrapolation par les méthodes polynomiales et de Fourier sont de nature complètement différente. L'extrapolation de Fourier ne peut être appliquée qu'au marché plat en raison de sa nature périodique (cette ligne est une somme de sinusoïdes de fréquence, de phase et d'amplitude différentes), et elle a toujours tendance à revenir en arrière,alors que l'extrapolation polynomiale, au contraire, est bonne pour la tendance, car elle essaie toujours de "voler vers le haut" ou vers le bas en raison de sa nature graduelle.
Il est donc logique de combiner ces deux méthodes pour obtenir de bons résultats d'extrapolation.
L'approximation polynomiale présente un intérêt particulier pour les programmeurs car ce type d'approximation est très bien optimisé et peut être calculé très rapidement. J'ai réussi à sortir des cycles pour le calcul des coefficients.
Il est également important de se rappeler que tous les types d'approximation créent des lignes redessinables avec chaque nouveau point. Seul le traceur de la ligne d'approximation n'est pas redessiné.
Une approximation polynomiale n'a qu'une seule solution, contrairement à une approximation de Fourier. Cela permet de créer des diapositives uniques non redimensionnables :
Je vois, deviner au hasard n'est pas mal non plus. Personne n'a donc résolu des problèmes similaires. Je vais le visualiser, je vais voir.
Personne ne l'a résolu - c'est faux. Toutes les méthodes d'interpolation ont leur justification théorique et généralement un objectif clair. Par exemple, le défaut cubique deux cannelures minimise l'énergie potentielle de la flexion élastique d'une règle passant par les clous martelés dans la planche aux nœuds de la cannelure. De cette façon, une courbe lisse (défaut inférieur à 3) a été obtenue à partir d'un tableau de points dans un dessin avec un contour de navire ou un profil d'aile. Les mêmes cannelures illustrent la déflexion d'une poutre multi-supports en mathématiques résilientes. Pour comparer les résultats de l'interpolation avec différents objectifs, on a besoin d'un objectif généralisé, un critère qui est calculable pour toute méthode d'interpolation. Il est basé sur le nombre de coefficients à déterminer. En gros, si une approximation polynomiale avec une augmentation du degré polynomial de 3 à 7 réduit la somme des carrés de l'écart de 20%, alors le degré 3 est plus raisonnable que 7. L'analogue en radiotechnique, si je ne me trompe pas, est la fréquence de coupure du filtre.
La chose la plus précieuse pour un trader n'est pas l'interpolation ou l'approximation, mais l'extrapolation.
Les splines ne conviennent pas à l'extrapolation.
J'ai une grande expérience et compréhension de l'approximation-extrapolation polynomiale. Moins d'expérience - Fourier.
L'extrapolation par les méthodes polynomiales et de Fourier sont de nature complètement différente. L'extrapolation de Fourier ne peut être appliquée qu'au marché plat en raison de sa nature périodique (cette ligne est une somme de sinusoïdes de fréquence, de phase et d'amplitude différentes), et elle a toujours tendance à revenir en arrière,alors que l'extrapolation polynomiale, au contraire, est bonne pour la tendance, car elle essaie toujours de "voler vers le haut" ou vers le bas en raison de sa nature graduelle.
Il est donc logique de combiner ces deux méthodes pour obtenir de bons résultats d'extrapolation.
L'approximation polynomiale présente un intérêt particulier pour les programmeurs car ce type d'approximation est très bien optimisé et peut être calculé très rapidement. J'ai réussi à sortir des cycles pour le calcul des coefficients.
Il est également important de se rappeler que tous les types d'approximation créent des lignes redessinables avec chaque nouveau point. Seul le tracé de la ligne d'approximation n'est pas redessiné.
Une approximation polynomiale n'a qu'une seule solution, contrairement à une approximation de Fourier. Cela permet de créer des diapositives uniques non redimensionnables :
C'est bien. Je n'ai rien à extrapoler, c'est l'interpolation qui est nécessaire. Je veux dire que cela n'a aucun sens de faire une prévision sur la base d'une telle extrapolation. Il est nécessaire que cette ligne soit aussi forte que possible, d'un côté à l'autre, comme votre ligne bleue. Et je veux pouvoir obtenir une solution sur les nouveaux points, oui (sans recalculer sur la base de la formule existante).
J'ai donc demandé ce qu'il valait mieux utiliser - des polynômes ou des splines ou d'autres sous-espèces. Et peut-être que le 10ème degré serait amusant aussi.
Personne ne l'a résolu - c'est faux. Toutes les méthodes d'interpolation ont leur justification théorique et généralement un objectif clair. Par exemple, le défaut cubique de deux cannelures minimise l'énergie potentielle de la flexion élastique d'une règle passant par des clous martelés dans la planche aux nœuds de la cannelure. De cette façon, une courbe lisse (défaut inférieur à 3) a été obtenue à partir d'un tableau de points dans un dessin avec un contour de navire ou un profil d'aile. Les mêmes cannelures illustrent la déflexion d'une poutre multi-supports en mathématiques résilientes. Pour comparer les résultats de l'interpolation avec différents objectifs, on a besoin d'un objectif généralisé, un critère qui est calculable pour toute méthode d'interpolation. Il est basé sur le nombre de coefficients à déterminer. En gros, si une approximation polynomiale avec une augmentation du degré polynomial de 3 à 7 réduit la somme des carrés de l'écart de 20%, alors le degré 3 est plus raisonnable que 7. L'analogue en radiotechnique, si je ne me trompe pas, est la fréquence de coupure du filtre.
C'est juste que si je commence à essayer d'expliquer tout ce que je vais faire avec, cela va encore faire quelques pages :) Vous avez besoin de variabilité, de différents degrés de polynômes, du nombre de points de grille, etc.
C'est bien. Je n'ai rien à extrapoler, c'est l'interpolation qui est nécessaire. En ce sens que faire une prévision sur une telle extrapolation n'a aucun sens par la suite. Il est nécessaire que cette ligne soit la plus forte possible, d'un côté à l'autre, comme votre ligne bleue. Et je veux pouvoir obtenir une solution sur les nouveaux points, oui (sans recalculer sur la base de la formule existante).
J'ai donc demandé ce qu'il valait mieux utiliser - des polynômes ou des splines ou d'autres sous-espèces. Et peut-être que le 10ème degré serait cool aussi.
L'interpolation exactement ? Vous êtes sûr ? Pas d'approximation ? Et ce n'est pas redessinable ?
Vous n'allez pas interpoler chaque tic.
Si vous avez besoin d'une interpolation sur des nœuds intermédiaires (nœuds ZigZag par exemple) sans redessiner, alors tout l'enjeu est de savoir où sera le nœud suivant.
Vous ne pouvez créer un Zig-Zag clair non redessinable que si vous disposez d'une machine à remonter le temps. Il est impossible de déterminer sans machine à remonter le temps que la barre actuelle est un extremum.
Il y a périodiquement quelqu'un sur le forum que j'appelle un "tireur de queue".
Le but est la queue de cheval.
C'est un classique du genre : décaler la SMA vers la gauche d'une demi-période et finir de dessiner ces demi-périodes comme par hasard avec un polynôme d'un certain degré. Par exemplehttps://www.mql5.com/ru/forum/224374. Vous l'avez probablement déjà vu.
Vous pouvez faire une très belle interpolation le long des extrema en zigzag avec des splines, mais vous devez bien comprendre qu'entre les deux ou trois derniers nœuds, il y aura un redécoupage. Il n'y a pas de solution sans elle !
S'il n'est pas redessiné, ce n'est pas une interpolation, mais ce que j'appelle un tracé de la ligne d'approximation (pas d'interpolation !).
A part les polynômes, je ne vois rien de compréhensible pour l'instant.
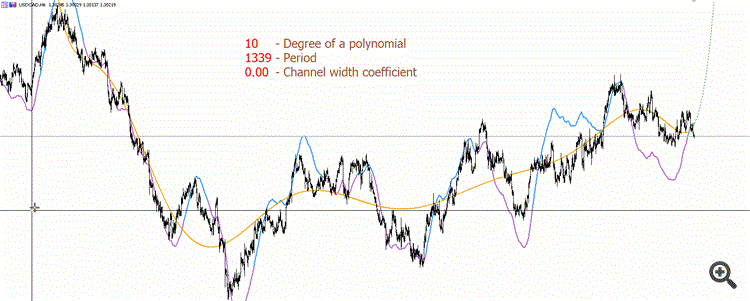
Voici un gif spécialement enregistré pour démontrer un exemple de polynôme de degré supérieur (10), afin de comprendre à quel point c'est beaucoup moins "beau" que je ne le voudrais :))
La ligne violette et bleue n'est pas redessinable. Le violet est le polynôme "regardant vers le bas", le bleu est le polynôme "regardant vers le haut".
Et il n'y a pas assez de précision pour calculer les polynômes de haut degré. Nous devrons utiliser des bibliothèques spéciales utilisant des types de précision supérieure. Le fait que le "traceur" commence à "sauter" à de petites périodes dans le gif - c'est la raison pour laquelle le double manque de précision.
Mais personnellement, je ne vois pas l'application pratique des polynômes de degré supérieur à 5.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
J'ai besoin d'interpoler une fonction avec des paramètres arbitraires, j'ai donc choisi les splines.
J'ai bien compris que j'obtiendrai des interpolants différents selon le nombre de points de nœud, que puis-je faire varier d'autre ?
Et la deuxième question, qu'est-ce qu'il vaut mieux choisir pour l'interpolation dans la liste, si j'ai juste besoin de construire de nombreuses interpolations différentes de la série originale (la variation est importante).