Discussion de l'article "Approche Économétrique de l'Analyse des Graphiques"

[MetaQuotes]

Un nouvel article Approche Économétrique de l'Analyse des Graphiques a été publié :

Cet article décrit les méthodes d'analyse économétriques, l'analyse d'auto-corrélation et l'analyse de variance conditionnelle en particulier. Quel est l'avantage de l'approche décrite ici? L'utilisation des modèles GARCH non linéaires permet de représenter formellement la série analysée du point de vue mathématique et de créer une prévision pour un nombre spécifié d'étapes.

Il est évident que l' objetde l'analyse est une série de prix (ses dérivés), qui est une time series.

Les économètres étudient les séries chronologiques du point de vue des méthodes fréquentielles (analyse spectrale, analyse par ondelettes) et des méthodes du domaine temporel (analyse de corrélation croisée, analyse d'auto-corrélation). L'article a été fourni au lecteur"Building Spectrum Analysis" qui décrit les méthodes de fréquence. Maintenant, je propose de jeter un œil aux méthodes du domaine temporel, à l'analyse d'auto-corrélation et à l'analyse de la variance conditionnelle en particulier.

Les modèles non linéaires décrivent mieux le comportement des price time series que les modèles linéaires. C'est pourquoi concentrons-nous sur l'étude des modèles non linéaires dans cet article.

Les séries chronologiques de prix ont des caractéristiques particulières qui ne peuvent être prises en compte que par certains modèles économétriques. Tout d’abord, de telles caractéristiques comprennent «fat tail» groupage de volatilité et effet de levier      

                                                                                                                

 

Figure 1. Distributions avec différents aplatissements.

Auteur : Denis Kirichenko

[Alexey Subbotin]

Une distribution dont l'insularité est inférieure à celle d'une distribution normale a un caractère de "normalité", c'est-à-dire qu'elle n'a pas de caractère de "normalité". «толстые хвосты»

Cette affirmation est fondamentalement erronée.

Premièrement, parlons en russe et appelons "kurtosis" et "insularité" par le terme accepté - coefficient de kurtosis ou simplement kurtosis.

Deuxièmement, l'"insularité" et les "queues grasses" n'ont en général aucun rapport entre elles. Voici un contre-exemple : la distribution de Laplace ( exponentielle bilatérale), à laquelle obéissent, il faut le dire, les graphiques de la grande majorité des séries chronologiques financières. Son excès est égal à 3 (c'est-à-dire que son sommet est plus net que celui de la distribution normale), mais ses queues sont épaisses - elles décroissent selon la loi exp(-x), c'est-à-dire plus lentement que celle de la gaussienne exp(-x^2).

[[Supprimé]]

alsu:

C'est fondamentalement faux.

Premièrement, parlons en russe et appelons "kurtosis" et "insularité" par le terme accepté - coefficient de kurtosis ou simplement kurtosis.

Deuxièmement, l'"insularité" et les "queues grasses" n'ont en général aucun rapport entre elles. Voici un contre-exemple : la distribution de Laplace (exponentielle bilatérale), à laquelle obéissent, il faut le dire, les graphiques de la grande majorité des séries chronologiques financières. Son excès est égal à 3 (c'est-à-dire que le sommet est plus net que dans la distribution normale), mais les queues sont simplement épaisses - elles diminuent selon la loi exp(-x), c'est-à-dire plus lentement que dans la gaussienne exp(-x^2).

En outre, il n'existe pas de concept d'"excès" en soi, mais un concept de "ratio d'excès", qui est une mesure d'un autre concept, celui d'"excès de distribution", et ce concept n'est défini que pour les distributions unimodales. Ainsi, pour utiliser ce coefficient à bon escient, il est nécessaire, premièrement, de déterminer la fonction de distribution empirique, ce qui n'est pas une tâche triviale du point de vue des mathématiques, et deuxièmement, dans le cadre de certains critères probabilistes, de vérifier et d'accepter l'hypothèse selon laquelle la distribution a un seul mode, ce qui n'est pas toujours le cas pour les séries financières et qui est également une tâche non triviale. Sans ces étapes, tout calcul ultérieur est impossible s'il nécessite le "coefficient d'excès".

P.S..

Rien n'est écrit sur ce qu'il faut faire si le test indique que la série n'est pas applicable au modèle supposé.

Rien n'est dit sur le pourquoi et le comment de l'utilisation d'une série de "rendements" et non d'une autre.

Dans la pratique, la principale raison pour laquelle il est préférable de travailler avec les rendements des actifs plutôt qu'avec les prix directs des actifs est que les rendements ont des propriétés statistiques plus intéressantes.

Lesquelles, attrayantes comment, et dans quel but ? Pourquoi attrayantes plutôt qu'opportunes ? Quel est un critère mathématique valable pour choisir le type de transformation ?

[Denis Kirichenko]

Chers collègues, je vous remercie de l'attention que vous portez à cet article. Dans la mesure du possible, j'essaierai de répondre à toutes les questions et critiques. Pour ma part, si le sujet vous intéresse, je vous invite à lire la littérature citée à la fin de l'article. De nombreuses questions disparaîtront d'elles-mêmes.

[Denis Kirichenko]

alsu:

...Parlons russe et appelons "kurtosis" et "islandness" par le terme accepté - coefficient d'excès ou simplement excès....

J'ai particulièrement apprécié le fait qu'alsu considère les mots "coefficient" et "excès" comme russes...

[Denis Kirichenko]

alsu:

Deuxièmement, l'"insularité" et les "queues grasses" ne sont généralement pas liées. Voici un contre-exemple : la distribution de Laplace (exponentielle bilatérale), à laquelle obéissent, il convient de le noter, les graphiques de la grande majorité des séries chronologiques financières. Son excès est égal à 3 (c'est-à-dire que le sommet est plus net que dans la distribution normale), mais les queues sont simplement épaisses - elles diminuent selon la loi exp(-x), c'est-à-dire plus lentement que dans la gaussienne exp(-x^2).

C'est exactement ce que je pense être généralement lié.

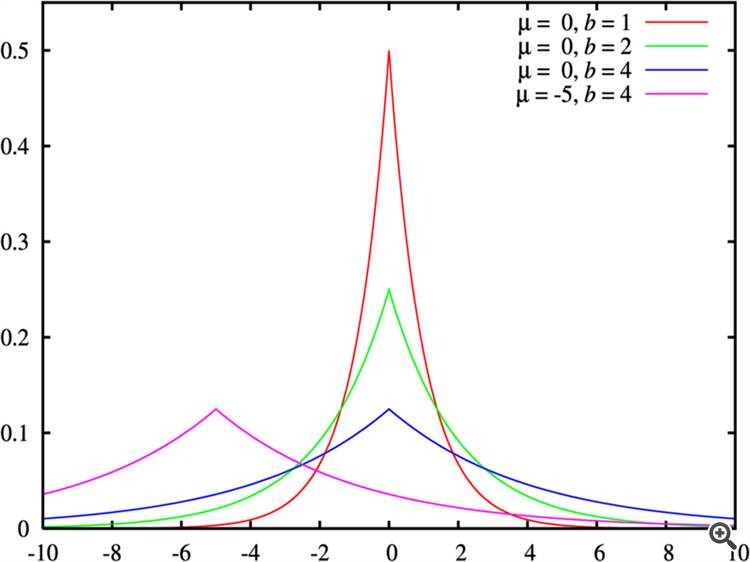
Un exemple de "moins d'aplatissement - queues plus épaisses" est présenté dans la figure "Distributions de Laplace avec différents paramètres".

[Denis Kirichenko]

J'ajouterais seulement la phrase suivante à mon article : "La distribution d'une série de rendements présente plus souvent un comportement de queue grasse que la distribution normale." Le phénomène des "fat tails" est appelé excès de kurtosis dans la littérature anglophone. Les séries dont les distributions présentent de telles queues sont appelées leptokurtiques, ayant un kurtosis positif (dépassant le kurtosis de la distribution normale).

Passons maintenant au coefficient d'aplatissement:

Ladistribution normale a une aplatissement nul, γ2 = 0.

Si les queues de la distribution sont plus "légères" et que le pic est plus net que celui de la distribution normale, alors γ2 > 0.

Si les queues de la distribution sont plus "lourdes" et que le pic est plus "aplati" que la distribution normale, alors γ2 < 0.

[Rashid Umarov]

denkir:

Je ne ferais qu'ajouter une telle suggestion à mon article :

Complétez-le. Nous republierons.

[[Supprimé]]

denkir:

J'ajouterais seulement la phrase suivante à mon article : "La distribution d'une série de rendements présente plus souvent un comportement de queue grasse que la distribution normale." Le phénomène des "fat tails" est appelé excès de kurtosis dans la littérature anglophone. Les séries dont les distributions présentent de telles queues sont dites leptokurtiques, ayant un kurtosis positif (dépassant le kurtosis de la distribution normale).

Passons maintenant au coefficient d'aplatissement:

Ladistribution normale a une aplatissement nul, γ2 = 0.

Si les queues de la distribution sont plus "légères" et que le pic est plus net que celui de la distribution normale, alors γ2 > 0.

Si les queues de la distribution sont plus "lourdes" et que le pic est plus "aplati" que la distribution normale, alors γ2 < 0.

Faux, et wiki contient des erreurs. Prenons la distribution uniforme. Son excès peut être calculé, et elle n'a pas de queue du tout. On vous a donc dit à juste titre que, dans le cas général, il n'y a pas de relation entre la gravité, la longueur, la présence même de queues et le coefficient d'aplatissement. Prenons une distribution triangulaire, c'est la même chose.

[ds2]

Pendant que vous discutez des termes, j'ai déjà construit du jour au lendemain quelques EA rentables en utilisant les idées de cet article. :-)

Cependant, leurs profits sont très faibles, bien qu'ils soient assez stables (vérifiés sur l'historique de 12 ans, les graphiques croissent magnifiquement). Les corrélations détectées par les méthodes décrites dans l'article sont plutôt faibles (les coefficients d'autocorrélation des séries sont d'environ 0,01, dans des cas exceptionnels approchant 0,1, en fonction des dérivés de prix qui sont corrélés), et lors de la négociation, le profit est fortement battu par le spread. J'ai dû ajouter un filtre pour n'effectuer des transactions qu'à l'arrivée de signaux forts, faute de quoi la courbe de rentabilité descendrait de manière quasi linéaire.

Merci à l'auteur en tout cas. Les idées sont précieuses. Je pense que les critiques ne devraient pas mettre le nez de l'auteur dans les abîmes de la mathématique, mais considérer l'article comme une indication d'un vaste champ d'expériences pratiques.

[[Supprimé]]

ds2:

Pendant que vous discutez des termes, j'ai déjà construit du jour au lendemain quelques EA rentables en utilisant les idées de cet article. :-)

Cependant, leurs profits sont très faibles, bien qu'ils soient assez stables (vérifiés sur l'historique de 12 ans, les graphiques croissent magnifiquement). Les corrélations détectées par les méthodes décrites dans l'article sont plutôt faibles (les coefficients d'autocorrélation des séries sont d'environ 0,01, dans des cas exceptionnels approchant 0,1, en fonction des dérivés de prix qui sont corrélés), et lors de la négociation, le profit est fortement battu par le spread. J'ai dû ajouter un filtre pour n'effectuer des transactions qu'à l'arrivée de signaux forts, faute de quoi la courbe de rentabilité descendrait de manière quasi linéaire.

Merci à l'auteur en tout cas. Les idées sont précieuses. Je pense que les critiques ne devraient pas mettre le nez de l'auteur dans les abîmes de la mathématique, mais considérer l'article comme une indication d'un vaste champ d'expériences pratiques.

Et pensez-vous que les critiques devraient être présents lors des soutenances de thèse, ou accepter la thèse sans défense et commencer la recherche pratique ? Je pense que vous serez intéressé de savoir que les corrélations ne sont pas calculées correctement. La critique a pour but d'améliorer le matériel, personne ne prétend que l'article est bon. Ainsi, le bénéfice sur vos systèmes ne sera pas faible, mais plus important.