Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Es obvio que q debe retirarse y sólo al final del periodo t. En todos los demás casos, el importe retirado será inferior a
El erizo ha decidido utilizar cálculos analíticos))))
El problema no tiene extremos, porque tenemos una serie numérica monotónicamente creciente, una función con un argumento en forma de tamaño del depósito. Es decir, no hay nada que optimizar. Cuanto mayor sea el argumento y t, mayor será el valor de la función. En cualquier otro caso, el valor de la función disminuirá.
Es difícil buscar un gato negro en una habitación oscura, sobre todo si no está allí (c) Confucio
Sólo queda tomar la derivada del tiempo y equipararla a cero... Sí.
Por cierto, en todo caso, la derivada debería tomarse sobre k
¡Perdón! Realmente en la k .
Reshetov:
Es obvio que hay que retirar q y sólo al final del periodo t. En todos los demás casos, el importe retirado será menor.
Yura, estás tan seguro de ti mismo que es gracioso cuando te equivocas.
En la primera página, avtomat dio una imagen donde se puede ver claramente el óptimo en el parámetro k . Tal vez no te hayas dado cuenta. Te mostraré otra:
¿Ves el máximo? ¿No? Pero está ahí.
Descansa, erizo.
¡No puede ser!...
¿Puede ser más específico? Es decir, en forma de fórmula.
En otras palabras, ¡el óptimo en términos de porcentaje de retirada es realmente visible!
Hace poco resolví un problema similar...
Y luego combinamos todo esto y obtenemos la función resultante de dos variables.
También hay que mencionar que el resultado depende del periodo de optimización, es decir
el óptimo para 12 meses no es igual a cuatro óptimos para períodos de 3 meses.
Hace poco resolví un problema similar...
Así es, avtomat. Así es exactamente como se comporta. Pero realmente necesito obtener una solución analítica para la fracción óptima de k. Si se toma la derivada de k de f(k), se obtiene la siguiente ecuación: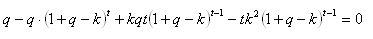
La figura siguiente muestra claramente que la abscisa donde df/dk es cero coincide con el máximo de f(k).
Pero, ¿cómo resolverlo con respecto a k?
De todos modos, el problema no tiene nada que ver con el comercio. Es un problema sobre el rentista. Sería muy apropiado para esa rama.
P.D. Me pregunto, ¿qué hará Jura en esta situación? Va a fingir que no se ha dado cuenta de nada (no hay máximo en el parámetro k ) y no va a dejar ningún comentario sobre el tema o tendrá que reconsiderar sus supuestos básicos de por vida...
P.D. Me pregunto qué hará Jura en esta situación. Hará como que no se da cuenta de nada (no hay máximo para el parámetro k ) y no dejará más comentarios sobre el tema o tendrá que reconsiderar sus principales puntos de ajuste de por vida...
Me han permitido utilizar un depósito de X0 rublos durante t meses. Cada mes el depósito recibe un porcentaje fijo q del valor actual del depósito X. Se me permite retirar de la cuenta un determinado porcentaje k cada mes que no supere el valor de q.
Se me permite abrir operaciones con el tamaño de lote HO. Cada operación positiva abierta tiene un u% de posibilidades de acumular w pips, mientras se gana q por supuesto del valor actual del depósito XO. Se me permite cerrar parcialmente una orden en un determinado porcentaje k tantas veces como desee (hasta el 100% de cierre) con una frecuencia de n pips que no exceda de w.
Pregunta: Encuentre en relación con u%, los valores óptimos de k, n.
Así es, avtomat. Así es exactamente como se comporta. Pero realmente necesito obtener una solución analítica para la fracción óptima de eliminación k. Si se toma la derivada de k de f(k), se obtiene la siguiente ecuación:
La figura siguiente muestra claramente que la abscisa donde df/dk es cero coincide con el máximo de f(k).
Pero, ¿cómo resolverlo con respecto a k?
si la ecuación anterior es cierta, entonces podemos hacerlo:
Pero, de nuevo, cuáles son los requisitos, cuáles son las condiciones...
q y t -- cantidades constantes dadas o ...