Funciones trigonométricas

MQL5 proporciona las tres funciones trigonométricas principales (MathCos, MathSin, MathTan) y sus inversas (MathArccos, MathArcsin, MathArctan). Todos ellos trabajan con ángulos en radianes. Para ángulos en grados, utilice la fórmula:

Aquí, M_PI es una de varias constantes con cantidades trigonométricas (pi y sus derivadas) integradas en el lenguaje.

La tangente del arco también puede calcularse para una cantidad representada por el cociente de dos coordenadas y y x: esta versión ampliada se denomina MathArctan2; es capaz de restituir ángulos en todo el rango del círculo de -M_PI a +M_PI, a diferencia de MathArctan, que se limita a -M_PI_2 a +M_PI_2.

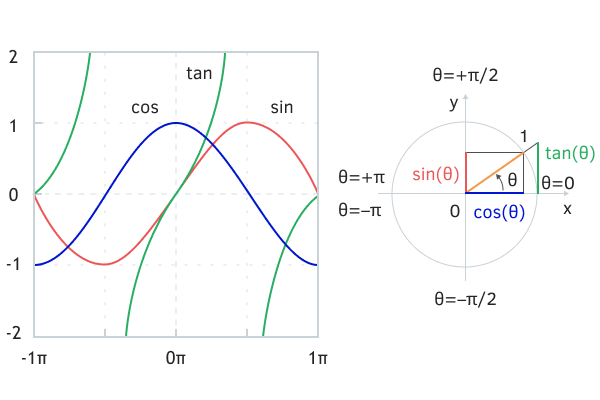
Funciones trigonométricas y cuadrantes del círculo unitario

Encontrará ejemplos de cálculos en el script MathTrig.mq5 (véase después de las descripciones).

double MathCos(double value) ≡ double cos(double value)

double MathSin(double value) ≡ double sin(double value)

Las funciones devuelven, respectivamente, el coseno y el seno del número pasado (el ángulo está en radianes).

double MathTan(double value) ≡ double tan(double value)

La función devuelve la tangente del número pasado (el ángulo está en radianes).

double MathArccos(double value) ≡ double acos(double value)

double MathArcsin(double value) ≡ double asin(double value)

Las funciones devuelven el valor, respectivamente, del arcocoseno y arcoseno del número pasado, es decir, el ángulo en radianes. Si x = MathCos(t), entonces t = MathArccos(x). El seno y el arcoseno tienen un esquema similar. Si y = MathSin(t), entonces t = MathArcsin(y).

El parámetro debe estar comprendido entre -1 y +1. En caso contrario, la función devolverá NaN.

El resultado del arcocoseno está en el rango de 0 a M_PI, y el resultado del arcoseno está entre -M_PI_2 y +M_PI_2. Los rangos indicados se denominan rangos principales, ya que las funciones son multivaloradas, es decir, sus valores se repiten periódicamente. Los semiperíodos seleccionados cubren completamente la zona de definición de -1 a +1.

El ángulo resultante para el coseno se encuentra en el semicírculo superior, y la solución simétrica del semicírculo inferior se puede obtener añadiendo un signo, es decir, t=-t. Para el seno, el ángulo resultante está en el semicírculo de la derecha, y la segunda solución en el semicírculo de la izquierda es M_PI-t (si para t negativo también se requiere obtener un ángulo adicional negativo, entonces -M_PI-t).

double MathArctan(double value) ≡ double atan(double value)

La función devuelve el valor de la tangente del arco para el número pasado, es decir, el ángulo en radianes, en el rango de -M_PI_2 a +M_PI_2.

La función es inversa a MathTan, pero con una salvedad.

Obsérvese que el período de la tangente es 2 veces menor que el período completo (circunferencia) debido a que la razón de seno y coseno se repite en cuadrantes opuestos (cuartos de circunferencia) por superposición de signos. Como resultado, el valor de la tangente por sí solo no es suficiente para determinar de forma unívoca el ángulo original en todo el rango de -M_PI a +M_PI. Para ello se puede utilizar la función MathArctan2, en la que la tangente se representa mediante dos componentes separados.

double MathArctan2(double y, double x) ≡ double atan2(double y, double x)

La función devuelve en radianes el valor del ángulo cuya tangente es igual al cociente de dos números especificados: coordenadas a lo largo del eje y y a lo largo del eje x.

El resultado (denominémoslo r) se encuentra en el intervalo de -M_PI a +M_PI, y para él se cumple la condición MathTan(r) = y / x.

La función tiene en cuenta el signo de ambos argumentos para determinar el cuadrante correcto (sujeto a condiciones límite, cuando x o y son iguales a 0, es decir, están en el límite de los cuadrantes).

• 1 – x >= 0, y >= 0, 0 <= r <= M_PI_2
• 2 – x < 0, y >= 0, M_PI_2 < r <= M_PI
• 3 – x < 0, y < 0, -M_PI < r < -M_PI_2
• 4 – x >= 0, y < 0, -M_PI_2 <= r < 0

A continuación se muestran los resultados de llamar a funciones trigonométricas en el script MathTrig.mq5.