三角函数

MQL5 提供了三个主要的三角函数 (MathCos, MathSin, MathTan) 以及它们的逆函数 (MathArccos, MathArcsin, MathArctan)。它们均处理以弧度为单位的角度。对于以度数为单位的角度，使用以下公式：

其中 M_PI 是语言内置的若干常量之一，具有三角函数数量（pi 及其��生值）。

也可以为由两个坐标 y 和 x 的比率表示的数量计算反正切值：该扩展版本称为 MathArctan2；它能够还原圆完整范围 -M_PI 到 +M_PI 内的角度，不同于 MathArctan，后者仅限于 -M_PI_2 到 +M_PI_2。

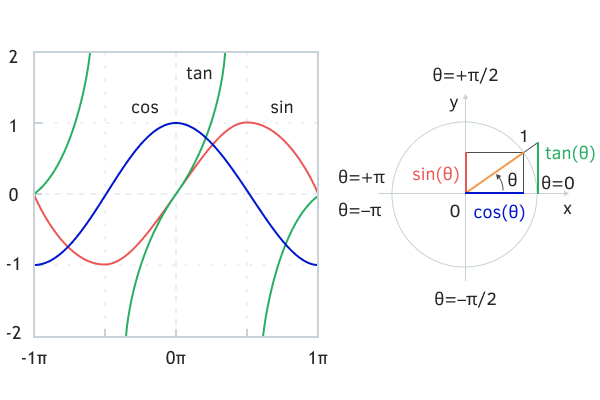
三角函数和单位圆的象限

计算示例在 MathTrig.mq5 脚本中提供（参见说明之后）。

double MathCos(double value) ≡ double cos(double value)

double MathSin(double value) ≡ double sin(double value)

这两个函数分别返回传递数字的余弦和正弦（角度以弧度为单位）。

double MathTan(double value) ≡ double tan(double value)

该函数返回传递数字的正切（角度以弧度为单位）。

double MathArccos(double value) ≡ double acos(double value)

double MathArcsin(double value) ≡ double asin(double value)

这两个函数分别返回传递数字的反余弦和反正弦，即弧度单位的角度。如果 x = MathCos(t)，则 t = MathArccos(x)。正弦和反正弦具有类似的方案。如果 y = MathSin(t)，则 t = MathArcsin(y)。

参数必须在 -1 到 +1 之间。否则，该函数将返回 NaN。

反余弦的结果在 0 到 M_PI 之间，而反正弦的结果在 -M_PI_2 到 +M_PI_2 之间。指示的范围称为主范围，因为函数是多值的，即它们的值定期重复。所选的半期间完全涵盖从 -1 到 +1 的定义区间。

得到的正弦的角度处于上半圆内，而下半圆中的对称解可通过添加一个符号获得，即 t=-t。对于正弦，获得的角度处于右半圆内，而左半圆内的第二解为 M_PI-t（若要求对负 t 也获取负的附加角，则解为 -M_PI-t）。

double MathArctan(double value) ≡ double atan(double value)

该函数返回传递数字的反正切值，即以弧度为单位的角度，范围在 -M_PI_2 到 +M_PI_2 之间。

该函数是 MathTan 的反函数，但有一个注意事项。

请注意，由于正弦和余弦的比率因符号叠加而在相反象限（圆的四分之一）中重复，正切的期间是全期间（圆周）的二分之一。因此，仅依靠正切值无法唯一确定从 -M_PI 到 +M_PI 的全范围上的原始角度。可以使用 MathArctan2 函数实现，其中正切由两个单独的分量表示。

double MathArctan2(double y, double x) ≡ double atan2(double y, double x)

该函数返回弧度单位的角度值，其正切值等于两个指定数字的比率：沿 y 和沿 x 轴的坐标。

结果（将其表示为 r）在 -M_PI 到 +M_PI 范围内，并且满足条件 MathTan(r) = y / x。

该函数考虑两个自变量的符号，以确定正确象限（遵循边界条件，当 x 或 y 等于 0，则它们处于象限的边界上）。

• 1 ― x >= 0, y >= 0, 0 <= r <= M_PI_2
• 2 ― x < 0, y >= 0, M_PI_2 < r <= M_PI
• 3 ― x < 0, y < 0, -M_PI < r < -M_PI_2
• 4 ― x >= 0, y < 0, -M_PI_2 <= r < 0

下面是在 MathTrig.mq5 脚本中调用三角函数的结果。