Discussion of article "Statistical Distributions in MQL5 - taking the best of R" - page 19

[Aleksey Nikolayev]

Aleksey Nikolayev:
There is a wish to add Kolmogorov distribution to the library. It is very useful because of its use in the Kolmogorov-Smirnov criterion and in the problem of searching for the decomposition of a random process.

I will leave it here just in case. Calculation of CDF and its additions for distribution of Kolmogorov-Smirnov statistic for two-sided one-sample test.

[Aleksey Nikolayev]

Has anyone used this?

[Renat Fatkhullin]

Aleksey Nikolayev:

CDF of hypergeometric distribution is incorrectly calculated by MathCumulativeDistributionHypergeometric() function. By definition, the probability distribution function must be defined for any real number. Below is a script on mql5 with its results and, for comparison, the same on R.

result:

-1.0 nan 2

0.0 0.0 0

0.5 nan 2

zero divide in 'Hypergeometric.mqh' (241,35)

Result:

[1] 0.0000000 0.0000000 0.0000000 0.2222222

You passed incorrect arguments and got ERR_ARGUMENTS_INVALID (2). We are checking the input parameters in more detail, and R appears to have replaced the answer with zeros.

//+------------------------------------------------------------------+
//| Hypergeometric cumulative distribution function (CDF) | |
//+------------------------------------------------------------------+
//| The function returns the probability that an observation |
//| from the Hypergeometric distribution with parameters m,n,k |
//| is less than or equal to x.|
//||
//| Arguments:|
//| x : The desired number of objects |
//| m : Size of the population |
//| k : Number of items with the desired characteristic |
//|| in the population|
//| n : Number of samples drawn |
//| tail : Flag to calculate lower tail |
//| log_mode : Logarithm mode,if true it calculates Log values |
//| error_code : Variable for error code |
//||
//| Return value:|
//| The value of the Hypergeometric cumulative distribution function |
//| with parameters m,n,k, evaluated at x. ||
//+------------------------------------------------------------------+
//| Based on algorithm by John Burkardt|
//+------------------------------------------------------------------+
double MathCumulativeDistributionHypergeometric(const double x,const double m,const double k,const double n,const bool tail,const bool log_mode,int &error_code)
  {
//--- check NaN
   if(!MathIsValidNumber(x) || !MathIsValidNumber(m) || !MathIsValidNumber(k) || !MathIsValidNumber(n))
     {
      error_code=ERR_ARGUMENTS_NAN;
      return QNaN;
     }
//--- m,k,n,x must be integer
   if(m!=MathRound(m) || k!=MathRound(k) || n!=MathRound(n) || x!=MathRound(x))
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- m,k,n,x must be positive
   if(m<0 || k<0 || n<0 || x<0)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- check ranges
   if(n>m || k>m)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }

[Renat Fatkhullin]

Aleksey Nikolayev:

Some (not all) binomial coefficients are negative, for example:

result: -309196571788882235

should be: 349615716557887488

Because of the large K (28) the 64-bit long overflowed there. The return value is long.

To count values within such limits, you need to rewrite the function to double values.

[Aleksey Nikolayev]

Renat Fatkhullin:

You passed incorrect arguments and got ERR_ARGUMENTS_INVALID (2). We check the input parameters in more detail, and R seems to have replaced the answer with zeros.

1) Any CDF - probability distribution function (discrete ones are no exception!) MUST DEFINITELY be defined for all real numbers. Below is an analogue of the code in R with its result, showing how this should count in reality. By the way, you have some discrete CDF functions counting correctly and some not.

2) For value 1 you get a division by zero error.

[Renat Fatkhullin]

Aleksey Nikolayev:

1) Any CDF - probability distribution function (discrete ones are no exception!) MUST DEFINITELY be defined for all real numbers. Below is an analogue of the code in R with its result showing how this should be considered in reality. By the way, some discrete CDF functions you have counted correctly and some you have not.

2) For value 1 you get a division by zero error.

Read the code of the function and its check, it is in the source code.

I don't have R at hand, I have to check it separately. I see division by zero, we need to understand the boundary conditions.

[Aleksey Nikolayev]

Renat Fatkhullin:

Because of a large K (28), the 64-bit long was overflowed there. The return value is long.

To count values within such limits, you should rewrite the function to double values.

It is clear. It's just that there is an error with the logarithm of the binomial coefficient at integer arguments and I thought that this was the reason. Now I've looked at the code and realised that I was wrong - the reason is something else.

#include <Math\Stat\Math.mqh>

void OnStart()
  { Print(MathBinomialCoefficientLog(62,28));
    Print(MathBinomialCoefficientLog(62.0,28.0));
  }

result:

test_clog (EURUSD.m,MN1) -nan(ind)

test_clog (EURUSD.m,MN1) 40.39561099351077

PS Wrong, the problem is also in overflow

[Aleksey Nikolayev]

Renat Fatkhullin:

There is no R at hand,

R online

[Denis Kirichenko]

Some trouble with NoncentralBeta. I took the script from the Documentation.

These are the results for different parameters.

[Denis Kirichenko]

Formula in Documentation:

Is the analogue in Wikipedia:

Looked at the code.

The MathRandomNoncentralBeta() function has lines like this:

//--- generate random number using Noncentral ChiSquare
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomNoncentralChiSquare(b2,lambda2,error_code);
result[i]=chi1/(chi1+chi2);

The same Wikipedia has this:

The noncentral beta distribution (Type I) is the distribution of the ratio

where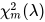 is anoncentral chi-squared random variable with degrees of freedom m and noncentrality parameter 𝜆 , and 𝜒 𝑛 2 is a centralchi-squared random variable with degrees of freedom n , independent of 𝜒 𝑚 2 ( 𝜆 ) .

That is, two random variables are taken, where the first is from a non-central chi-squared distribution and the second is from a central one. Probably the code can be corrected to this:

//--- generate random number using Noncentral ChiSquare
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomChiSquare(b2,error_code);
result[i]=chi1/(chi1+chi2);

The modified graphs in the example will be below.