To the author (no nickname for some reason).
The same problem can be solved in other ways. There are tests for redundant and missing variables. I could do that and compare with your results. But I need all your files in .csv format.
...I need all your files in .csv format.
I think the source is in the masterdata.zip archive.
After we have chosen the variables, we will have to make some relationship from them, in which price will be the dependent variable (function), and the other indicators will be independent variables. Here is the schematic equation:
price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 means the previous value. This is natural since the indicator is derived from price analytically. Let's take into account that price is an increment, so we will take the increments of indicators. Because of laziness, I do not take all the indicators. Let's estimate this equation by the method of least squares:
We have obtained an estimate of the coefficients of the equation. The last column is very interesting: it means the probability that the corresponding coefficient is equal to zero. This probability for all the coefficients is much higher than at least 10%, i.e. we can consider that we cannot reject the hypothesis that the corresponding coefficients are equal to zero. Accordingly, the R-squared has a ridiculous value.
I conclude that it is useless to deal with the classification of indicators - they are useless because they have nothing to do with price increment.
Or am I wrong?
...Or am I wrong?
I think you're right :-)
faa1947, I have a question for you. I wanted to clarify a couple of things... this is how I calculated the data from your equation:
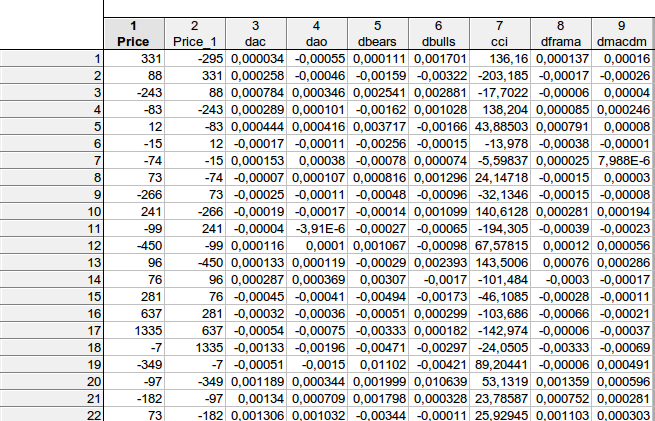
Does the data from the table match your schematic equation price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
And got the following result:
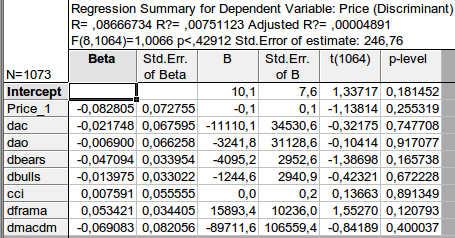
Once we have chosen the variables, we will have to make some relationship from them, in which price will be the dependent variable (function) and the other indicators will be the independent variables. Here is a schematic equation:
price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 means the previous value. This is natural since the indicator is derived from price analytically. Let's take into account that price is an increment, so we will take the increments of indicators. Because of laziness, I do not take all the indicators. Let's estimate this equation by the method of least squares:
We have obtained an estimate of the coefficients of the equation. The last column is very interesting: it means the probability that the corresponding coefficient is equal to zero. This probability for all the coefficients is much higher than at least 10%, i.e. we can consider that we cannot reject the hypothesis that the corresponding coefficients are equal to zero. Accordingly, the R-squared has a ridiculous value.
I conclude that it is useless to deal with the classification of indicators - they are useless because they have nothing to do with price increment.
Or am I wrong?
Please provide the name of the statistical method you used. It was the construction of a linear regression equation, where the input is the indicators and the output is the future price? Is that correct? This will not work for forex as it is not a linear deterministic system. Discriminant analysis has a different task, it builds models for pattern recognition based on external descriptions of the system.
If classifying indicators to analyse price increments was useless, then technical analysis would be meaningless. Fortunately, the price does not behave chaotically, it has a memory of previous events.
You seem to be right :-)
faa1947, I have a question for you. I wanted to clarify a couple of things... this is how I calculated the data from your equation:
Does the data from the table match your schematic equation price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
And got the following result:
The raw data looks as follows:
The equations look like this:
Estimation Equation:
=========================
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
Substituted Coefficients:
=========================
PRICE = -0.0228102658125*PRICE(-1) + 12005.8974278*DAC(-1) + 4033.10946937*DAO(-1) + 3176.11232129*DBEARS(-1) - 6021.36196728*DBULLS(-1) - 0.102710105369*CCI(-1) - 11487.4273249*DFRAMA(-1) + 62535.3387412*DMACDM(-1)
I don't understand your calculation. I have the principle of using the lag value (previous value). This makes it possible to make a prediction. If lag -1 corresponds to the 1st observation, then the dependent variable corresponds to a new, predicted, unobserved observation.
What is p-level? For me, it is the probability that the corresponding coefficient is zero.
Please provide the name of the statistical method you used. Was it a linear regression equation where the input is the indicators and the output is the future price? Is that correct?
The regression was estimated using the least squares method. It can be used to make predictions.
This will not work for forex as it is not a linear deterministic system.
If linear, it is in a specific example. It is not deterministic because even the coefficients are treated as random variables. All coefficients are not calculated, but estimated. The second column shows the standard error of coefficient estimation. Please note that it is huge.
If the classification of indicators for analysing price increments was useless, technical analysis would be meaningless.
Exactly so, and I dare to assure you that I am not the only one who thinks so. TA is not a science, but a type of astrology. Originally, 300 years ago, it was a system for visualising the kotir. It has evolved enormously since then. Everything else is for the Pinocchios in the field of miracles. I was happy with your article, as it has some regular and repeatable thought.
If the classification of indicators for analysing price increment was useless
Here we have analysed a special case of indicators. It is always necessary to prove that a particular indicator or its use has something to do with a quote. TA never considers this issue.
Fortunately, the price does not behave chaotically, it has a memory of previous events.
All econometrics is built on the assumption that a quote has a deterministic component (autocorrelation, memory) and noise.
Discriminant analysis has a different task, it builds models for pattern recognition based on external descriptions of the system.
The task is clear. But whether the result obtained can be trusted, that is the question. The problem is not classification (that is part of the problem, which also needs to be solved), but trust in the resulting prediction. That is exactly the problem.
I don't understand your calculation. My principle is to use the lag value (previous value). This makes it possible to make a prediction. If lag -1 corresponds to the 1st observation, then the dependent variable corresponds to a new, predicted, unobserved observation.
What is p-level? For me, it is the probability that the corresponding coefficient is zero.
faa1947, I have given the table with lags (for the first few rows - I can't fit the whole table). But first I calculated the indicator differences, so the total number of rows is 1073 instead of 1074. Then I moved the dependent variable Price one step forward.
It turned out that, on the example of the 1st line:
331 = C(1)*(-295) + C(2)* 0.000034+ C(3)* (-0.00055) + C(4)* 0.000111 + C(5)* 0.001701+ C(6)*136.16+ C(7)* 0.000137+ C(8)*0.00016, provided that
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
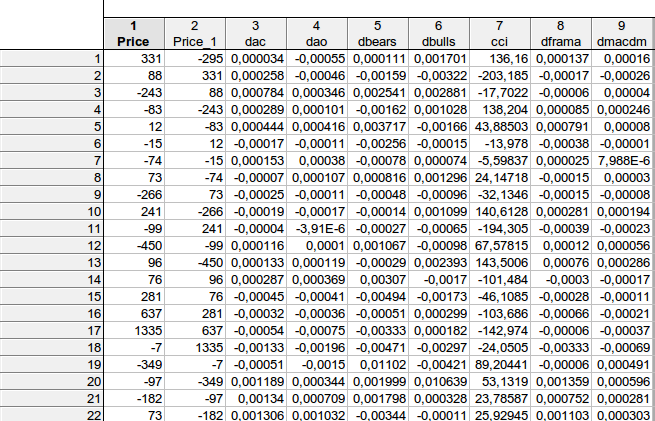
In general, I approximately got a similar result - there is no way to reject the null hypothesis that the considered coefficients are equal to zero...
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
New article Using Discriminant Analysis to Develop Trading Systems is published:
When developing a trading system, there usually arises a problem of selecting the best combination of indicators and their signals. Discriminant analysis is one of the methods to find such combinations. The article gives an example of developing an EA for market data collection and illustrates the use of the discriminant analysis for building prognostic models for the FOREX market in Statistica software.
Author: ArtemGaleev