Thanks for the interesting article.
It's a pity that there are few explanations on codes.
And something is wrong with the python code, I have installed all libraries, but it gives the following in the terminal:
learning time = 1228.5106182098389
solver = lbfgs
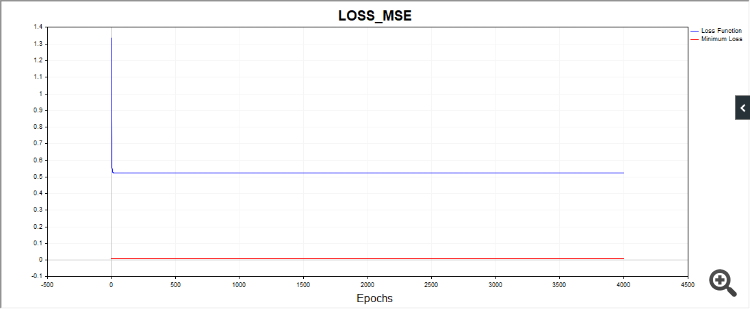
loss = 0.0024399556870102
iter = 300
C:\Users\User\AppData\Local\Programs\Python\Python39\lib\site-packages\sklearn\neural_network\_multilayer_perceptron.py:545: ConvergenceWarning: lbfgs failed to converge (status=1): in '' (0,0)
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. in '' (0,0)
Increase the number of iterations (max_iter) or scale the data as shown in: in '' (0,0)
https://scikit-learn.org/stable/modules/preprocessing.html in '' (0,0)
self.n_iter_ = _check_optimize_result("lbfgs", opt_res, self.max_iter) in '' (0,0)
Traceback (most recent call last): in '' (0,0)
plt.plot(np.log(pd.DataFrame(clf.loss_curve_))) in 'SklearnMLP.py' (59,0)
AttributeError: 'MLPRegressor' object has no attribute 'loss_curve_' in 'SklearnMLP.py' (59,0)
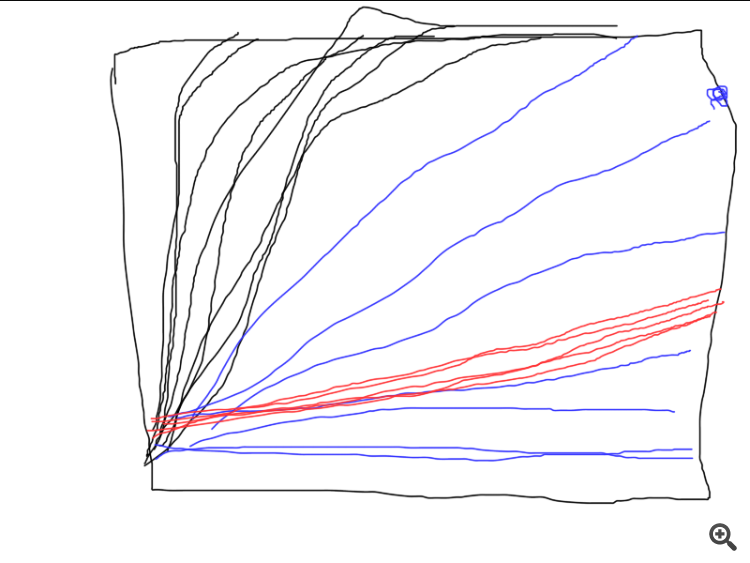
One more thing, the SD script in some cases draws such a picture:
I.e., the algo is stuck on, apparently, a simple date.
Other codes also produce very different convergence results. Therefore, it is desirable to give graphs of a series of independent tests, pictures of single tests tell us little (practically nothing).
Thanks for the feedback.
On python. It is not an error, it warns that the algorithm has stopped because we have reached the iteration limit. That is, the algorithm stopped before the value tol = 0.000001 was reached. And then it warns that the lbfgs optimiser does not have a "loss_curve" attribute, i.e. loss function data. For adam and sgd they do, but for lbfgs for some reason they don't. I probably should have made a script so that when lbfgs is started it would not ask for this property so that it would not confuse people.
On SD. Since we start each time from different points in the parameter space, the paths to the solution will also be different. I have done a lot of testing, sometimes it really takes more iterations to converge. I tried to give an average number of iterations. You can increase the number of iterations and you will see that the algorithm converges in the end.
On SD. Since we start each time from a different point in the parameter space, the paths to converge to a solution will also be different. I have done a lot of testing, sometimes it really takes more iterations to converge. I tried to give an average number of iterations. You can increase the number of iterations and you will see that the algorithm converges in the end.
That's what I'm talking about. It's the robustness, or, reproducibility of the results. The greater the scatter of results, the closer the algorithm is to RND for a given problem.
Here's an example of how three different algorithms work. Which one is the best? Unless you run a series of independent tests and calculate the average results (ideally, calculate and compare the variance of the final results), it is impossible to compare.
That's what I'm talking about. It is the stability, or, reproducibility of the results. The greater the scatter of results, the closer the algorithm is to RND for a given problem.
Here's an example of how three different algorithms work. Which one is the best? Unless you run a series of independent tests and calculate the average results (ideally, calculate and compare the variance of the final results), it is impossible to compare.
Then it is necessary to define the evaluation criterion.
No, in this case you don't have to go to such trouble, but if you are comparing different methods, you could add one more cycle (independent tests) and plot the graphs of individual tests. Everything would be very clear, who converges, how stable it is and how many iterations it takes. And so it turned out to be "like last time", when the result is great, but only once in a million.
Anyway, thanks, the article gave me some interesting thoughts.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Check out the new article: Training a multilayer perceptron using the Levenberg-Marquardt algorithm.
The purpose of this article is to provide practicing traders with a very effective neural network training algorithm - a variant of the Newtonian optimization method known as the Levenberg-Marquardt algorithm. It is one of the fastest algorithms for training feed-forward neural networks, rivaled only by the Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm.
Stochastic optimization methods such as stochastic gradient descent (SGD) and Adam are well suited for offline training when the neural network overfits over long periods of time. If a trader using neural networks wants the model to quickly adapt to constantly changing trading conditions, he needs to retrain the network online at each new bar, or after a short period of time. In this case, the best algorithms are those that, in addition to information about the gradient of the loss function, also use additional information about the second partial derivatives, which allows finding a local minimum of the loss function in just a few training epochs.
At the moment, as far as I know, there is no publicly available implementation of the Levenberg-Marquardt algorithm in MQL5. It is time to fill this gap, and also, at the same time, briefly go over the well-known and simplest optimization algorithms, such as gradient descent, gradient descent with momentum, and stochastic gradient descent. At the end of the article, we will conduct a small test of the efficiency of the Levenberg-Marquardt algorithm and algorithms from the scikit-learn machine learning library.
Author: Evgeniy Chernish