MathKurtosis(), what actually return?

New comment
 
What does MathKurtosis() function actually return?

a) Kurtosis, K = M4 / s^4

or

b) Excess, Ex = K − 3

where,

M4 = fourth central moment

s^4 = standard deviation to the fourth power


thx in adv

Best regards,

Koval

 
funkykoval:
What does MathKurtosis() function actually return?

a) Kurtosis, K = M4 / s^4

or

b) Excess, Ex = K − 3

where,

M4 = fourth central moment

s^4 = standard deviation to the fourth power


thx in adv

Best regards,

Koval

Here is a full explanation


https://www.investopedia.com/terms/k/kurtosis.asp

Kurtosis Definition, Types, and Importance
Kurtosis Definition, Types, and Importance
  • www.investopedia.com
Kurtosis is a statistical measure used to describe a characteristic of a dataset. When normally distributed data is plotted on a graph, it generally takes the form of a bell. This is called the bell curve. The plotted data that are furthest from the mean of the data usually form the tails on each side of the curve. Kurtosis indicates how much...
 

Thanks, I know what Kurtosis is and what it comes with.

I'm just not sure what the function in MQL5 actually returns, does it return Kurtosis or maybe Excess?

Do you know the answer?

I need this to determine the type of data distribution (e.g. Platykurtic)


Best regards

Koval

 
funkykoval #: Thanks, I know what Kurtosis is and what it comes with. I'm just not sure what the function in MQL5 actually returns, does it return Kurtosis or maybe Excess? Do you know the answer? I need this to determine the type of data distribution (e.g. Platykurtic)

Did you refer to the documentation? ... https://www.mql5.com/en/search#!keyword=MathKurtosis&module=mql5_module_documentation

 

oh, thanks a lot Fernando.

here https://www.mql5.com/en/docs/standardlibrary/mathematics/stat/array_stat/mathkurtosis

is a link to https://www.r-tutor.com/elementary-statistics/numerical-measures/kurtosis

I looks, like function returning Excess of Kurtosis (not Kurtosis) :) 

Best regards,

Koval

Documentation on MQL5: Standard Library / Mathematics / Statistics / Statistical Characteristics / MathKurtosis
Documentation on MQL5: Standard Library / Mathematics / Statistics / Statistical Characteristics / MathKurtosis
  • www.mql5.com
MathKurtosis(const double&) - Statistical Characteristics - Statistics - Mathematics - Standard Library - MQL5 Reference - Reference on algorithmic/automated trading language for MetaTrader 5
 
funkykoval #:

oh, thanks a lot Fernando.

here https://www.mql5.com/en/docs/standardlibrary/mathematics/stat/array_stat/mathkurtosis

is a link to https://www.r-tutor.com/elementary-statistics/numerical-measures/kurtosis

I looks, like function returning Excess of Kurtosis (not Kurtosis) :) 

Best regards,

Koval

It seems you overlooked some of the details in the documentation, on the very MQL5 document link you provided.

It states and I quote ...

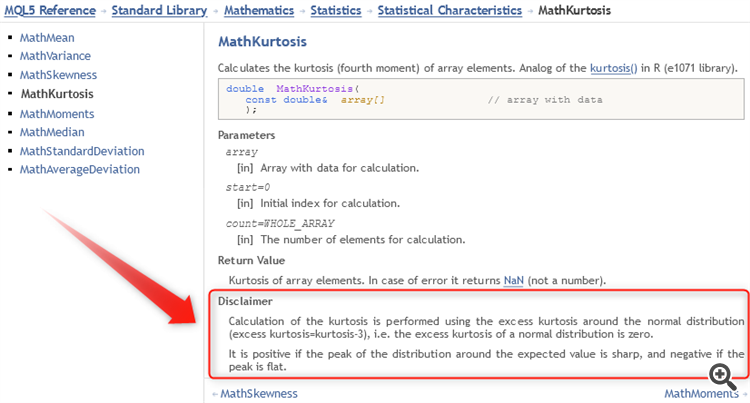
"Disclaimer

Calculation of the kurtosis is performed using the excess kurtosis around the normal distribution (excess kurtosis=kurtosis-3), i.e. the excess kurtosis of a normal distribution is zero.

It is positive if the peak of the distribution around the expected value is sharp, and negative if the peak is flat."


 

As usual, you are invaluable Fernando.

Thank you for being so understanding and willing to help.

Now I'm 100% clear, and in the future I have to read the documentation more carefully.

Thank you,

Koval

New comment