Renter - page 16
You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
It is interesting to see how these parameters affect the outcome:
For example, for our baseline conditions, at different valve positions, we get these interesting pictures
.
.
.
That's for the big picture...
We are interested in the last dependence
("a-da" phase profile -- the last graph is a special case of it)
It didn't work out very well. I won't post the calculations here. There is nothing beautiful about them.
I tried to use the following observation: 1+q-k = 1+epsilon, epsilon being a small value. Then I expanded the derivative by k in Taylor's series, first holding terms up to the third order of smallness. Then, after simplifications, we got the cubic equation. I discarded the third-order smallest term and tried to solve the resulting quadratic one. I failed: the discriminant is positive only at small t.
I'm afraid that I made a mistake by rejecting the cubic term: although it is a term of the third order of smallness in epsilon, it is not small. I had it as follows: epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3). It can be seen that for large t it can be quite small (even if epsilon~0.01 is quite a realistic assumption). And one does not want to solve the cubic one.
Let's see what Oleg gets.
P.S. Assuming epsilon*t = O(1) (or q*t = O(1) ), you can approximate the power function by an exponent. Let's give it a try.
There is another approach - without Taylor series, but simply by tangent method (Newton, I think). And one can get to a fairly exact analytical solution, too.
The point is that initially the conditions do not contain continuous time, but a lattice function -- i.e. a proper transformation must first be performed. Only then will the introduction of a small epsilon be valid. These are the properties of lattice functions.
By the way, it was the translation to the continuous time region that I dealt with in the first step of solving the problem, using the Laplace transform in the chain discretes--frequencies--time. To be more exact: also by this...
So, the object of our further analysis is the function
.
And I don't want to solve the cubic one.
Alexey, I have never seen an analytical expression for the roots of a cubic equation (except for partial simplified cases). Don't you have such an expression? Just like for a quadratic equation: x1=b/2+SQRT()... etc. Post it if you know it. I haven't found anything on the Internet. I remember from school, that there is even a representation of roots through harmonic functions!
There is another approach - without Taylor series, but simply by the tangent method (Newton, I think). And one can get to a fairly exact analytical solution, too.
Is it really possible to get an approximate solution in analytical form in this way? Never heard of it. Very interesting, I would like to see an example of the method.
Let's go to studio!
Yes, you talk about the solution obtained for large t. This is also of practical interest as a case of "unkillable" deposit. For what t did you manage to get an approximation? Maybe a limit transition for t->inf is possible. Then we may get analytical expression for optimal payout percentage, k, as a function of only one parameter q - value of accrued interest. This would be a great result.
avtomat:
The point is that the initial conditions do not contain continuous time, but a lattice function -- i.e. a conversion must first be made. Only then would the introduction of a small epsilon be valid. These are the properties of lattice functions.
By the way, it was the translation to the continuous time region that I dealt with in the first step of solving the problem, using the Laplace transform in the chain discretes--frequencies--time. To be more exact: including this...
Oleg, why do you think that the analytical expression obtained above for the sum of derivable means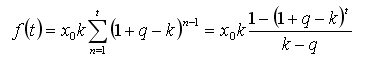
is not marginal for continuous time? After all, we didn't stipulate the minimum interval (step) limit of the original time series (iterated form of writing in the first post of the topic). If so, it is enough that at the limit transition at dt->0 we have a certain df(t) and there is no contradiction...
Oleg, why do you think that the above analytical expression for the sum of derivatives is not the limit for continuous time? After all, we didn't specifically stipulate a restriction on the minimum interval (step) of the original time series (iterated form of notation in the first post of the topic). If so, then it is enough that at the limit transition at dt->0 we have a definite df(t) and there is no contradiction...
Not so... Try to introduce a small epsilon here...
Yes, we haven't specifically stipulated anywhere, but the wording of the problem itself implicitly implies the use of a lattice function.
This means that the matching will be in the nodes of the lattice. Moreover, for lattice functions there are no intermediate points - only the nodes of the lattice. So all attempts to construct intermediate values will lead to erroneous results (by the way, these issues belong to the field of signal quantization). The intermediate values can be constructed by increasing the sampling rate, i.e. introducing again a lattice function with more nodes, which will not fundamentally change the essence of the phenomenon. This means, in particular, that first, second, etc. derivatives are used instead of first, second, etc. differences. Instead of integrals -- sums. ... etc. -- this is a whole field of study.
But there are ways of moving from one field to another and back again.
In this particular case of our problem, this approach does not suit us. So the first thing we have to do is to move from discrete time to continuous time.
The point is that the initial conditions are not continuous time, but a lattice function - i.e. a transformation must first be performed.
I've never seen an analytical expression for the roots of a cubic equation (except for partial simplifications). Don't you have one? Just like for a quadratic equation: x1=b/2+SQRT()... etc. Post it if you know it. I can't find anything on the Internet.
Cardano's formula.
I remember from school that there is even a representation of roots through harmonic functions!
The trigonometric formula of Viets
... Or not to produce, but to use the available apparatus of discrete version of Laplace transform, i.e. Z-transformation. Don't you think it would be simpler?
That's not the problem. At the very beginning there is a three-dimensional picture of "%growth - %yield - yield" - everything is already calculated, and it is in the discrete domain.
Now the sporting task is to present it all in an analytical form ;)
Cardano formula
Vyet's trigonometric formula