Renter

New comment
 

Hello all!

I have been allowed to use a deposit of X0 rubles for t months. Every month a fixed percentage q of the current value of the deposit X is deposited. I'm allowed to withdraw a percentage k from the account every month, but it doesn't exceed the value of q.

So the task is to maximize the amount of money withdrawn over a period of t months. It seems obvious that withdrawing the whole accrued interest q every month is not the best option, because in this case the deposit does not grow and with less load on the account, the eventually withdrawn amount may be larger... On the other hand, the value of k should not go to zero, because in this case the amount withdrawn would also go to zero. Apparently, the truth is somewhere in the middle. But where exactly?

Help me solve this problem analytically in a general way.

P.S. Did not post in a branch of zadacha not related to trade, because the proposed topic is related to the latter.

 
It seems that you have to make equality of equations and then differentiate them (the problem reminds of an ambulance, when you can take a shortcut in a field at a low speed, or drive on asphalt at a higher speed but on a longer route - at what point do you exit the asphalt into the field?)
 

So the question is, how do you make them up? So far it only works in iterative form:


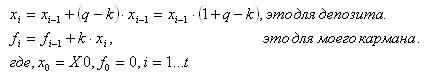
We need to present it in analytical form (as a functional dependence on time t).

 
Further expand the formula for f, i.e. bring it to fi = fi(x0).
 

Aha! Then it turns out like this:

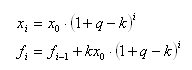
And the expression for the amount of money withdrawn over a period of t months can be written as:

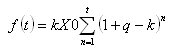
If so, that's better. What next? You have to get rid of the amount...

 

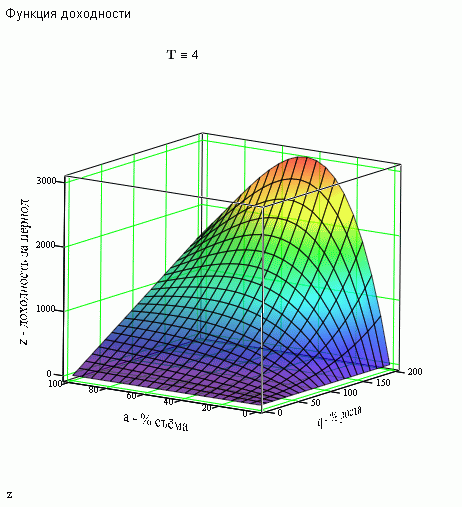
would look something like this.

 

No way!...

Can you be more specific? I mean in the form of a formula.

So you can really see the optimum in terms of the percentage of removal!

 
Neutron:

If so, that's better. What's next? We have to get rid of the sum...

Remember the formula for the sum of the first n terms of a geometric progression


 
where q is the denominator of the GP, b1 is the first term
 
alsu:

recall the formula for the sum of the n first terms of a geometric progression



Shaitan! Indeed, .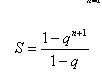

Then finally, the expression for the sum of the withdrawn funds will be given as:

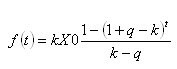
All that remains is to take the time derivative and equate it to zero... Yeah.

 
Neutron:

Hello all!

I have been allowed to use a deposit of X0 rubles for t months. Every month the deposit gets a fixed percentage q of the current value of the deposit X. I am allowed to withdraw some percentage k from the account every month which does not exceed the value of q.

So the problem is to maximise the amount of money withdrawn over a period of t months.

It is obvious that the amount to be withdrawn is q and only at the end of period t. In all other cases the amount withdrawn will be less.
12345678910111213141516171819202122232425262728293031
New comment
Reason: