Fitting a parabola
If you want to fit a parabola (y=ax^2+bx+c) to e.g. the last 3 values of a buffer, you need to solve a system of 3 linear equations. In software like Matlab or R that is really easy to do, but how would you do it in mql4? I guess there is no function for this?
- a trading strategy based on Elliott Wave Theory
- Not the Grail, just a regular one - Bablokos!!!
- Algorithm Optimisation Championship.
Here's my code for a general least squeares. You want Cog.degree=2 Cog.bars=3
//+------------------------------------------------------------------+ //| Center of Gravity | //+------------------------------------------------------------------+ void OnInitCOG(){ #define Cog.Degree.MAX 10 // ComputeCOG #define Cog.Degree.2MAX 20 // 2*MAX if (Cog.Degree < 1 || Cog.Degree > Cog.Degree.MAX) { Alert("Cog.Degree must be 1-", Cog.Degree.MAX); Log( "Cog.Degree must be 1-", Cog.Degree.MAX); Cog.Degree = MathMax(1, MathMin(Cog.Degree.MAX, Cog.Degree)); } if (Cog.Bars < Cog.Degree){ Alert("Cog.Bars must be ",Cog.Degree," or greater"); Log( "Cog.Bars must be ",Cog.Degree," or greater"); Cog.Bars = Cog.Degree; } if (Cog.NW0.LW1 < 0 || Cog.NW0.LW1 > 1){ Alert("Cog.NW0.LW1 must be 0 or 1"); Log( "Cog.NW0.LW1 must be 0 or 1"); Cog.NW0.LW1 = 0; } } #define COGCENTR 0 #define COGRMS 1 #define COGVALUES 2 double cog.values[][COGVALUES]; void ComputeCOG(int iBar) { /* The no repainting variant of the COG indicator "JB Center of Gravity.mq4" * was created by "ANG3110@latchess.com and Jürgen Bouché" * http://juergen.bouche.de Original indicator code from NG3110@latchess.com * * This creates a Nth degree least squares polynominal * 0 1 2 3 4 5 6 7 8 * EXn E1=bars EX E(X2) E(X3) E(X4) E(X5) E(X6) E(X7) E(X8) * * Aii 0 1 2 3 4 Bi * 0 E1=bars Ex E(x2) E(x3) E(x4) 0 EY ( )( ) ( ) * 1 Ex E(x2) E(x3) E(x4) E(x5) 1 E(YX) ( )( ) ( ) * 2 E(x2) E(x3) E(x4) E(x5) E(x6) 2 E(YX2) (Aii)(X)=(Bi) * 3 E(x3) E(x4) E(x5) E(x6) E(x7) 3 E(YX3) ( )( ) ( ) * 4 E(x4) E(x5) E(x6) E(x7) E(x8) 4 E(YX4) ( )( ) ( ) ******************************************************************************/ int nBars = GetBars(), iLimit = MathMin(nBars, iBar+Cog.Bars); if (iLimit-iBar < Cog.Degree) return; // Bad call or no bars. if (!ResizeBuffer(cog.values, nBars)) return; // Out of memory? double Bi[Cog.Degree.MAX]; double EXn[Cog.Degree.2MAX]; int Cog.Degree2 = Cog.Degree*2; double Aii[Cog.Degree.MAX, Cog.Degree.MAX]; for(int ii = 0; ii <= Cog.Degree; ii++) Bi[ii] = 0; for( ii = 0; ii <= Cog.Degree2; ii++) EXn[ii] = 0; for(int i = iBar; i < iLimit; i++){ // Count up for maximum accuracy if (Cog.NW0.LW1 == 0) double Xn = 1; else Xn = iLimit-i; // 1*weight for(ii = 0; ii <= Cog.Degree; ii++, Xn *= i){ Bi[ii] += Xn*GetOpen(i); EXn[ii] += Xn; } for( ; ii <= Cog.Degree2; ii++, Xn *= i) EXn[ii] += Xn; } for(int jj = 0; jj <= Cog.Degree; jj++) { for(ii = 0; ii <= Cog.Degree; ii++) { Aii[ii, jj] = EXn[ii + jj]; } } for(int kk = 0; kk <= Cog.Degree; kk++) { // Gaussian Elimination int ll = kk; double mm = MathAbs(Aii[ll, kk]); for(ii = kk+1; ii <= Cog.Degree; ii++) { // Largest magintude. double tt = MathAbs(Aii[ii, kk]); if (tt > mm) { ll = ii; mm = tt; } } if (ll != kk) { // Pivot. for(jj = 0; jj <= Cog.Degree; jj++) { tt = Aii[kk, jj]; Aii[kk, jj] = Aii[ll, jj]; Aii[ll, jj] = tt; } tt = Bi[kk]; Bi[kk] = Bi[ll]; Bi[ll] = tt; } for(ii = kk + 1; ii <= Cog.Degree; ii++) { // Reduce. double qq; qq = Aii[ii, kk] / Aii[kk, kk]; // Aii[ii,kk]=0 for(jj = kk+1; jj <= Cog.Degree; jj++) { Aii[ii, jj] -= qq * Aii[kk, jj]; } Bi[ii] -= qq * Bi[kk]; } } double x[Cog.Degree.MAX]; // Back substitution x[Cog.Degree] = Bi[Cog.Degree] / Aii[Cog.Degree, Cog.Degree]; for (ii = Cog.Degree-1; ii >= 0; ii--) { tt = Bi[ii]; for(jj = ii+1; jj <= Cog.Degree; jj++){ tt -= Aii[ii, jj] * x[jj]; } x[ii] = tt/Aii[ii, ii]; } // Least squares completed. Compute residual and final values. double Ews = 0, Ew = 0, w = 1.; for(i = iBar; i < iLimit; i++){ double Y = x[0]; for(kk = 1, Xn=i; kk <= Cog.Degree; kk++, Xn *= i) Y += x[kk] * Xn; double residual = MathMax(GetHigh(i) - Y, Y - GetLow(i)); if (Cog.NW0.LW1 == 1) w = iLimit-i; Ews += w * residual*residual; Ew += w; } double ms = Ews / Ew, rms = MathSqrt(ms); for(i = IfI(iLimit-1, iBar, Show.COG.Repaint); i >= iBar; i--){ Y = x[0]; for(kk = 1, Xn=i; kk <= Cog.Degree; kk++, Xn *= i) Y += x[kk] * Xn; cog.values[i][COGCENTR] = Y; cog.values[i][COGRMS] = rms; } return; } // ComputeCOG
thanks WHRoeder.
Hi WHRoeder. I incorporated your code but some doubts appeared. Could you give a light?
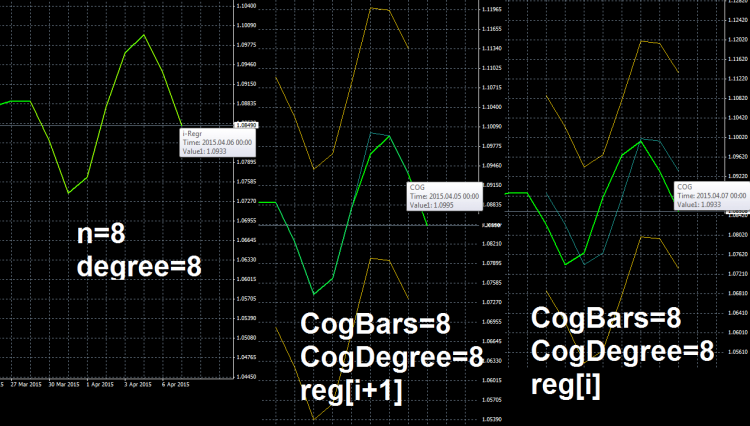
CogDegree is equal to CogBars but the line generated is not yet exact as the line graph. Why?
The image compares i-regr (that fits perfect) with my COG with reg[i] and reg[i+1].
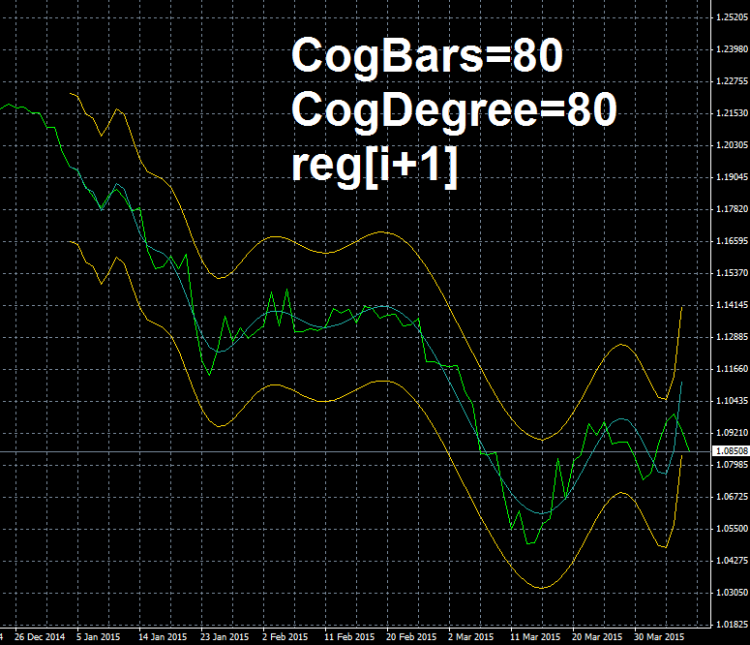
The maximum CogDegree that I got was 80, is this a limit?
CogDegreeMAX more than 253 has the alert "the size of local variables is too large (more than 512kb)", and more than 355 the line disappears, is it another limit?
Thanks by the info
My code:
#property indicator_chart_window #property indicator_buffers 3 #property indicator_color1 LightSeaGreen #property indicator_color2 Gold #property indicator_color3 Gold //----- double reg[],reg1[],reg2[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int init() { SetIndexBuffer(0, reg); SetIndexBuffer(1, reg1); SetIndexBuffer(2, reg2); SetIndexStyle(0, DRAW_LINE); SetIndexStyle(1, DRAW_LINE); SetIndexStyle(2, DRAW_LINE); return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int start() { int CogDegree=80; int CogBars=80; int CogNW0LW1; #define CogDegreeMAX 200 // ComputeCOG #define CogDegree2MAX 400 // 2*MAX #define COGCENTR 0 #define COGRMS 1 #define COGVALUES 2 double cogvalues[][COGVALUES]; if (CogDegree < 1 || CogDegree > CogDegreeMAX) { Alert("CogDegree must be 1-", CogDegreeMAX); // Log( "CogDegree must be 1-", Cog.Degree.MAX); CogDegree = MathMax(1, MathMin(CogDegreeMAX, CogDegree)); } if (CogBars < CogDegree){ Alert("CogBars must be ",CogDegree," or greater"); // Log( "CogBars must be ",Cog.Degree," or greater"); CogBars = CogDegree; } if (CogNW0LW1 < 0 || CogNW0LW1 > 1){ Alert("CogNW0LW1 must be 0 or 1"); // Log( "CogNW0LW1 must be 0 or 1"); CogNW0LW1 = 0; } int iBar; int nBars = iBars(NULL,0), iLimit = MathMin(nBars, iBar+CogBars); // if (iLimit-iBar < CogDegree) return; // Bad call or no bars. // if (!ResizeBuffer(cogvalues, nBars)) return; // Out of memory? double Bi[CogDegreeMAX]; double EXn[CogDegree2MAX]; int CogDegree2 = CogDegree*2; double Aii[CogDegreeMAX, CogDegreeMAX]; for(int ii = 0; ii <= CogDegree; ii++) Bi[ii] = 0; for( ii = 0; ii <= CogDegree2; ii++) EXn[ii] = 0; for(int i = iBar; i < iLimit; i++){ // Count up for maximum accuracy if (CogNW0LW1 == 0) double Xn = 1; else Xn = iLimit-i; // 1*weight for(ii = 0; ii <= CogDegree; ii++, Xn *= i){ Bi[ii] += Xn*iOpen(NULL,0,i); EXn[ii] += Xn; } for( ; ii <= CogDegree2; ii++, Xn *= i) EXn[ii] += Xn; } for(int jj = 0; jj <= CogDegree; jj++) { for(ii = 0; ii <= CogDegree; ii++) { Aii[ii, jj] = EXn[ii + jj]; } } for(int kk = 0; kk <= CogDegree; kk++) { // Gaussian Elimination int ll = kk; double mm = MathAbs(Aii[ll, kk]); for(ii = kk+1; ii <= CogDegree; ii++) { // Largest magintude. double tt = MathAbs(Aii[ii, kk]); if (tt > mm) { ll = ii; mm = tt; } } if (ll != kk) { // Pivot. for(jj = 0; jj <= CogDegree; jj++) { tt = Aii[kk, jj]; Aii[kk, jj] = Aii[ll, jj]; Aii[ll, jj] = tt; } tt = Bi[kk]; Bi[kk] = Bi[ll]; Bi[ll] = tt; } for(ii = kk + 1; ii <= CogDegree; ii++) { // Reduce. double qq; qq = Aii[ii, kk] / Aii[kk, kk]; // Aii[ii,kk]=0 for(jj = kk+1; jj <= CogDegree; jj++) { Aii[ii, jj] -= qq * Aii[kk, jj]; } Bi[ii] -= qq * Bi[kk]; } } double x[CogDegreeMAX]; // Back substitution x[CogDegree] = Bi[CogDegree] / Aii[CogDegree, CogDegree]; for (ii = CogDegree-1; ii >= 0; ii--) { tt = Bi[ii]; for(jj = ii+1; jj <= CogDegree; jj++){ tt -= Aii[ii, jj] * x[jj]; } x[ii] = tt/Aii[ii, ii]; } // Least squares completed. Compute residual and final values. double Ews = 0, Ew = 0, w = 1.; for(i = iBar; i < iLimit; i++){ double Y = x[0]; for(kk = 1, Xn=i; kk <= CogDegree; kk++, Xn *= i) Y += x[kk] * Xn; double residual = MathMax(iHigh(NULL,0,i) - Y, Y - iLow(NULL,0,i)); if (CogNW0LW1 == 1) w = iLimit-i; Ews += w * residual*residual; Ew += w; } double ms = Ews / Ew, rms = MathSqrt(ms); for(i = iLimit-1; i >= iBar; i--){ Y = x[0]; for(kk = 1, Xn=i; kk <= CogDegree; kk++, Xn *= i) Y += x[kk] * Xn; cogvalues[i][COGCENTR] = Y; cogvalues[i][COGRMS] = rms; reg[i+1] = Y; reg1[i+1] = Y + 2*rms; reg2[i+1] = Y - 2*rms; } return(0); } //+------------------------------------------------------------------+
noob01:
The maximum CogDegree that I got was 80, is this a limit?
CogDegreeMAX more than 253 has the alert "the size of local variables is too large (more than 512kb)", and more than 355 the line disappears, is it another limit?
You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register