Diskussion zum Artikel "Datenwissenschaft und maschinelles Lernen (Teil 11): Naïve Bayes, Wahrscheinlichkeitsrechnung im Handel"
alles ist gut und wunderbar, aber das einzige ist, dass die genommenen Indikatoren nicht unabhängig sind, sie sind gegenseitige Umsetzung von ein und derselben Sache. Von den Messwerten eines Indikators kann man auf die anderen schließen, und die Formeln sind bekannt.
Bayes wird nichts tun.
Es einfach herunterzuladen und in einem Testprogramm laufen zu lassen, ist ein bisschen mühsam. In dem Artikel habe ich keine Anweisungen gefunden "zu lehren, drücken Sie X"
Etwas für Akademiker wieder.
alles ist gut und schön, nur sind die genommenen Indikatoren nicht unabhängig, sondern eine gegenseitige Umsetzung ein und desselben Sachverhalts. Aus den Messwerten des einen kann man die anderen ableiten, und die Formeln sind bekannt
Bayes wird nichts bewirken.
Ich habe an der Universität Wahrscheinlichkeiten studiert, als ich meinen Abschluss in Finanzplanung gemacht habe.
Ich habe beim Handel nie Wahrscheinlichkeiten im Sinne der traditionellen "Wahrscheinlichkeitsformel""Wahrscheinlichkeit = Anzahl der günstigen Ergebnisse / Gesamtzahl der Ergebnisse" zur Analyse verwendet, obwohl ich das wahrscheinlich tun sollte!
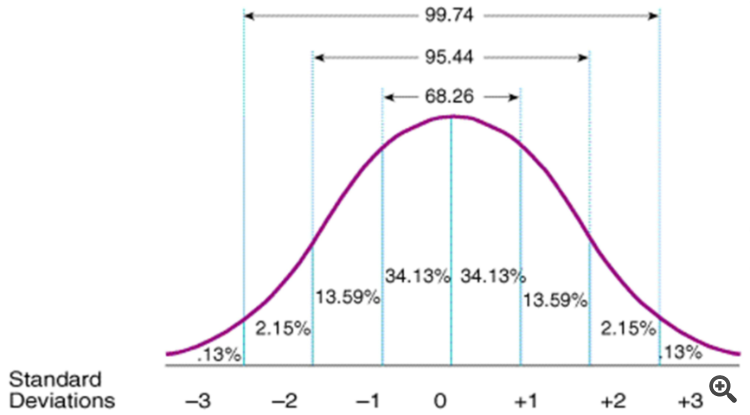
Realistisch betrachtet sind Standardabweichungen jedoch genau das: Sie geben die Abweichung (und damit die Wahrscheinlichkeit einer Umkehrung oder Fortsetzung) von Trades vom Mittelwert innerhalb eines bestimmten Zeitraums an. (d.h. wenn sich der Kurs SD1 nähert, besteht eine 68%ige Wahrscheinlichkeit, dass er zum Mittelwert zurückkehrt, wenn er SD2 erreicht hat, eine 95,5%ige Wahrscheinlichkeit und SD3 eine 99,7%ige Wahrscheinlichkeit), so dass Standardabweichungen sehr nützlich sein können, wenn es darum geht, abzuschätzen, wann Handelspositionen wahrscheinlich in die entgegengesetzte Richtung drehen werden, insbesondere wenn man so etwas wie einen Standardabweichungskanal verwendet.
Ich kann mir aber durchaus vorstellen, dass Wahrscheinlichkeiten bei der Analyse neuronaler Netze im Rahmen des ANN-Trainings und der Reflexion eingesetzt werden können!
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Datenwissenschaft und maschinelles Lernen (Teil 11): Naïve Bayes, Wahrscheinlichkeitsrechnung im Handel :
Der Handel mit Wahrscheinlichkeiten ist wie ein Drahtseilakt - er erfordert Präzision, Ausgewogenheit und ein ausgeprägtes Risikobewusstsein. In der Welt des Handels ist die Wahrscheinlichkeit alles. Das ist der Unterschied zwischen Erfolg und Misserfolg, Gewinn und Verlust. Indem sie sich die Macht der Wahrscheinlichkeit zunutze machen, können Händler fundierte Entscheidungen treffen, Risiken effektiv verwalten und ihre finanziellen Ziele erreichen. Ob Sie nun ein erfahrener Anleger oder ein Anfänger sind, das Verständnis der Wahrscheinlichkeit ist der Schlüssel zur Entfaltung Ihres Handelspotenzials. In diesem Artikel werden wir die aufregende Welt des Handels mit Wahrscheinlichkeiten erkunden und Ihnen zeigen, wie Sie Ihr Handelsspiel auf die nächste Stufe heben können.
Der Naïve Bayes-Klassifikator ist ein probabilistischer Algorithmus, der beim maschinellen Lernen für Klassifizierungsaufgaben verwendet wird. Sie basiert auf dem Bayes-Theorem, mit dem die Wahrscheinlichkeit einer Hypothese anhand der verfügbaren Beweise berechnet wird. Dieser probabilistische Klassifikator ist ein einfacher, aber effektiver Algorithmus für verschiedene Situationen. Dabei wird davon ausgegangen, dass die für die Klassifizierung verwendeten Merkmale unabhängig voneinander sind. Zum Beispiel: Wenn Sie möchten, dass dieses Modell Menschen (männlich und weiblich) anhand von Größe, Fußgröße, Gewicht und Schulterlänge klassifiziert, behandelt dieses Modell alle diese Variablen als unabhängig voneinander. In diesem Fall geht es nicht einmal davon aus, dass Fußgröße und Größe bei einem Menschen zusammenhängen.
Da sich dieses Modell nicht darum kümmert, die Muster zwischen den unabhängigen Variablen zu verstehen, denke ich, dass wir einen Versuch wagen sollten, es zu nutzen, um fundierte Handelsentscheidungen zu treffen. Ich glaube, dass im Handelsbereich ohnehin niemand die Muster vollständig versteht, also schauen wir mal, wie sich Naïve Bayes schlägt.
Autor: Omega J Msigwa