- Program types and their construction features
- Statistical analysis and fuzzy logic tools
- OpenCL: Parallel computations in MQL5
- Integration with Python
Statistical analysis and fuzzy logic tools
The MetaEditor development environment provides a separate type of include files with the mqh extension, which enable the exchange of frequently used code blocks. MetaQuotes delivers MetaTrader 5 with a vast Standard Library, which includes classes and methods for implementing a wide variety of tasks. This includes classes available for analyzing data using mathematical statistics and fuzzy logic.
The library of mathematical statistics offers functionality for working with basic statistical distributions. It has more than twenty distributions and five features are presented for each:
1. Calculation of distribution density.
2. Calculation of probabilities.
3. Calculation of distribution quantiles.
4. Generation of random numbers with a given distribution.
5. Calculation of theoretical distribution moments.
The library also allows you to calculate the statistical characteristics of a given data set. With the help of this library, one can easily perform statistical analysis of a sample from the historical data of the analyzed instrument. You can also compare the statistical indicators of several instruments and observe the dynamics of the statistical indicators of one instrument based on historical data from different time intervals.
Additionally, one can conduct a multifaceted and comprehensive analysis, and use its results as the foundation for building one's trading system.
Before discussing the capabilities of the fuzzy logic library, let us consider the concept itself. The concept of fuzzy logic was proposed by American scientist Lotfi Zadeh in 1965. This innovation allows the addition of a certain share of subjectivity inherent in real life to calculations. After all, you'll agree that when describing certain objects and processes, we often use vague and approximate reasoning.
We often hear the phrase "Words are used out of context." This suggests that the interpretation of words and their use in speech is highly dependent on the context. It is also difficult to describe a single candlestick on a chart. We can tell what color it is and mention the presence of shadows. But you'll agree, with such a description, we can divide all candlesticks into two classes based on their color. In fuzzy logic theory, these would be two sets.
Candlesticks
For further description, we will need to introduce additional concepts and measurements. We can compare a candlestick with neighboring candlesticks, calculate some kind of average, or take some kind of benchmark and compare to it. In doing so, we again get an inaccurate description. The deviation from our benchmark or average can vary, just as the influence of a factor can change significantly depending on the size of this deviation. The application of fuzzy logic allows us to solve this problem by introducing "fuzzy" set boundaries.
Three stages are distinguished in the history of fuzzy systems development:
- 1960-70s: development of theoretical aspects of fuzzy logic and fuzzy sets;
- 1970s-80s: the first practical results in the field of fuzzy systems control;
- From the 1980s to the present day: the creation of various software packages for constructing fuzzy systems significantly broadens the application scope of fuzzy logic.
Let us review the basic concepts of fuzzy set theory.
First, it is a fuzzy set, that is, a set of values unified by some rules.
The mathematical description of these rules is combined into a membership function which is a characteristic of a fuzzy set and is denoted by MFC(x) — the degree of the x value membership in the fuzzy set C.
The set of values of initial data satisfying the membership function is called the term set.
A collection of fuzzy sets and their rules are combined into a fuzzy model (system).
The results of the fuzzy model operation are determined from a combination of fuzzy sets using a system of fuzzy logical inferences. The MQL5 fuzzy logic library implements the Mamdani and Sugeno fuzzy logic inference systems.
To understand the differences between the usual mathematical description and the fuzzy logic membership function, let us consider an example of the description of a Doji candlestick (a candlestick without a body). Such candlesticks often act as harbingers of a trend change, as they appear in the area of supply and demand equilibrium.
In practice, it's rare to encounter a candlestick with a zero body size, where the opening price equals the closing price with mathematical precision. Therefore, some sort of tolerance is used when specifying a Doji. For example, let's assume that a Doji candlestick is any candlestick with a body of no more than 5 pips.
With such an assumption, using conventional logic, candlesticks with a body size of 1 point and 4 points will be classified as Doji and will have the same value for the strategy being used. At the same time, a candlestick with a body of 6 pips will no longer fall into the Doji category and will be ignored by the strategy. Why is it that a deviation of 3 points in the first case (4 - 1 = 3) doesn't matter, but a smaller deviation of 2 points (6 - 4 = 2) in the second case makes a fundamental difference? The application of fuzzy logic can smooth out these angles and account for deviations in both cases.
The figure below shows the chart of assigning a candlestick to the Doji class (set) depending on the length of the candlestick body. The red line represents the classical mathematical logic with the previously accepted allowance, and the green line reflects the rule of fuzzy logic. As we can see from the graph, the use of fuzzy logic rules will allow us to make decisions depending on the strength level of the incoming signal. For instance, if the candlestick body is larger and approaches the boundaries of the fuzzy set, we can reduce the risk for the operation or even ignore such a signal.
Mathematically, the function showing the membership of a candlestick in the Doji fuzzy set can be represented as:
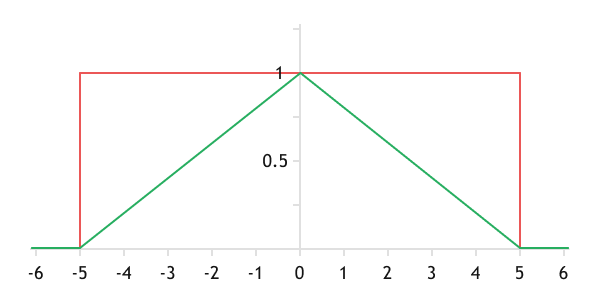
Graph of assigning a candle to the Doji class (red - mathematical logic, green - fuzzy logic)
In this case, we have obtained a special case of the symmetric triangular activation function. To define it, in fact, we needed only one parameter a which stands for boundary of the the range of 5 points. The center of the distribution is at point 0. In the general case, to define a triangular membership function, three parameters are required: the lower bound, the center, and the upper bound of the fuzzy set.
There are other membership functions, but the most widespread are the aforementioned triangular, trapezoidal, and Gaussian membership functions. Meanwhile, the triangular and trapezoidal functions can be symmetric (when the left and right zones of boundary fuzziness are equal) and asymmetric.
The graph of a trapezoidal function differs from the graph of a triangular function by the presence of a plateau in the upper part. To define such a function, four points are required, indicating the upper and lower boundaries of the left and right zones of fuzziness. Between the blur zones, the function takes the value 1, and to the left and right of these zones, it takes the value 0. For instance, let's introduce a rule to determine the size of the body of an average candlestick with a body size ranging from 5 to 15 points and a fuzziness boundary zone of 5 points. The mathematical notation of such a rule will take the form:
Thus, we have already defined the second rule for the candlestick body. It is common to show the set of rules for a single variable on a single graph. In the chart below, the red triangular term represents the Doji candlestick, and the green trapezoidal term represents the average candlestick.
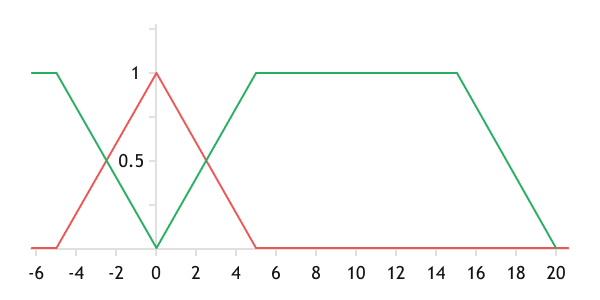
The aggregate term sets of Doji (red) and the average statistical candlestick (green).
Please note that on the graph, there is no sharp division between the Doji and the average candlestick at the 5-point mark, as it would be with threshold classification. Instead, we have a line crossing at about 2.5 points. In this case, the membership function will take a value of about 0.5. This means that a candlestick with a body of 2.5 points is equally applicable to the fuzzy Dodgy and medium candlestick sets. In such a case, secondary factors should be looked at to determine the controlling influence.
Continuing such iterations, we can describe the rules for a candlestick with a large body, as well as add rules for the candlestick shadows. Once we have done the work of defining the rules for describing candlesticks and their components, we will be able to describe various candlestick patterns with ease. For example, we can use fuzzy logic tools to describe a pin bar in quite a simple way by definition: a candlestick with a long one shadow, a small body, and a small or absent second shadow.
Note that using the rules of fuzzy logic allows us to move from clear values to some abstract definitions and approximate reasoning inherent in human logic. Therefore, the concepts of linguistic and fuzzy variables are introduced in fuzzy logic theory.
The linguistic variable has:
- A name, in the above examples it is "Candlestick Body";
- A set of its values referred to as the base termset. In our case, these are the Doji, Medium (regular) and Large candlesticks;
- A set of permitted values;
- A syntactic rule that describes terms using natural language words;
- A semantic rule defining the correspondence between the values of a linguistic variable and a fuzzy set of valid values.
In general practice, the fuzziness of the boundaries of fuzzy sets allows us to consider the natural symbiosis of the influence of different forces in the areas of their intersection. It also allows us to account for the fact that the effect of the force fades as the distance from the source of the impact increases.
The presence of fuzzy rules is an important, but not the sole, part of constructing a model. The process of fuzzy model building can be divided into three conventional stages:
1. Selecting baseline data
2. Defining a knowledge base (set of rules)
3. Defining the fuzzy logic inference method
It is quite natural that the entire construction process depends on the initial stage: the determination of the set of source data influences both the overall possibility of their classification and the number of possible classes (terms). Consequently, the set of rules (as well as their filling) for defining fuzzy sets is also determined based on the set of permitted values and the task at hand. It should be noted that even for the same set of input data, the underlying term set and rule set may vary depending on the task at hand.
Very often the parameters of the rules for defining fuzzy sets are strongly influenced by the subjective knowledge and experience of the model architect. Therefore, the practice of hybrid models has become widespread. In them, the parameter selection of rules is carried out by a neural network during its training on a training dataset.
Based on the created knowledge base, a fuzzy logic inference system is defined in the model. Fuzzy logical inference is the process of obtaining a fuzzy set that corresponds to the current input values, using fuzzy rules and fuzzy operations.
A number of logical operations have been developed for fuzzy sets, just as for regular sets. The main ones are union (fuzzy OR) and intersection (fuzzy AND). There is a general approach to performing fuzzy intersection, union, and complement operations.
To build the process of fuzzy logical inference, the MQL5 library offers the implementation of two main methods: Mamdani and Sugeno.
When using the Mamdani method, the value of the output variable is defined by a fuzzy term. The fuzzy rule of this method can be described as follows:
Where:
- X = a vector of input variables
- Y = an output variable
- a = a vector of initial data
- d = a value of the output variable
- W = the rule weight
In the Sugeno method, unlike Mamdani, the value of the output variable is determined not by a fuzzy set but by a linear function of the input data. The rule of this method is of the form:
where b is the vector of weights at free terms of the output value function.