非常好的作品!
我一下子就读完了。
谢谢!
文章值得称赞,谢谢 :)
我 在上帝的 帮助下制作了 LLM DeepSeek。你可以用自己的数据代替。
解释
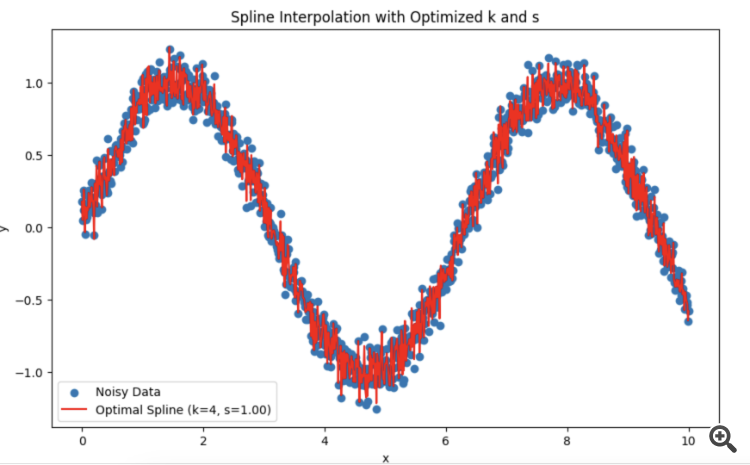
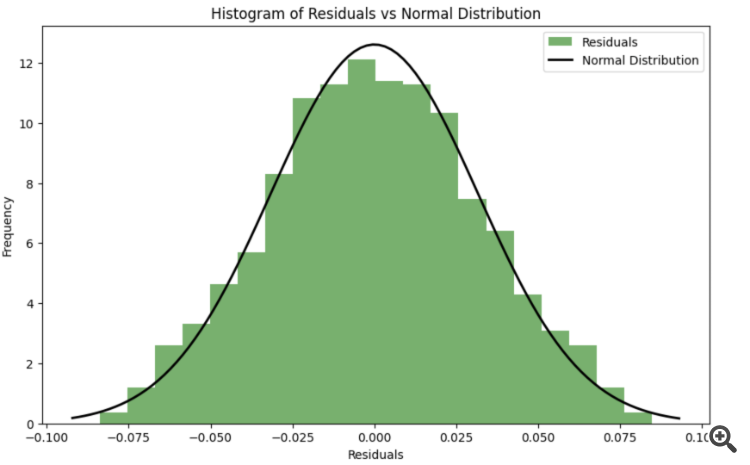
在优化过程中,为了使残差尽可能接近正态分布,可以使用一致准则(如 Shapiro-Wilk 准则或 Kolmogorov-Smirnov 准则)来评估残差的正态性。然后可以优化 参数 k k 和 s s, 使 残差与正态分布的偏差最小。
-
考虑残差正态性的误差函数:引入了一个新 函数 spline_error_with_normality,用于计算残差并使用 Shapiro-Wilk 准则评估残差的正态性。负 p 值最小化,残差的正态性最大化。
-
优化: 根据 新的误差函数对 参数 k k 和 s s 进行 优化。
这种方法可以调整样条曲线参数,使残差最大化为正态分布,从而提高模型的质量和结果的可解释性。
由于样条函数对新数据不起作用,因此可以在 HP 或其他滤波器下重做。如果希望建立一个特定的模型。
新文章 用于预测波动性的计量经济学工具:GARCH模型已发布:
文章描述了条件异方差非线性模型(GARCH)的特性。在GARCH模型的基础上,构建了iGARCH指标来预测未来一步的波动性。该模型参数的估计使用了ALGLIB数值分析库。
波动性是衡量金融资产价格变动性的一个重要指标。在分析报价时,人们早已注意到,大幅度的价格变动往往会导致更大的变动,尤其是在金融危机期间。相反,小幅度的变动之后通常跟随着小幅度的价格变动。因此,平稳期之后往往会出现相对不稳定的时期。
首个尝试解释该现象的模型是ARCH,由Engle提出— 即自回归条件异方差(异质性)模型。除了集群效应(将收益分为大值和小值的群组)外,该模型还解释了重尾和正峰度的出现,这是所有价格增量分布的共同特征。ARCH条件高斯模型的成功催生了一系列其推广模型。这些推广模型的目的是为金融时间序列分析中观察到的其他多种现象提供解释。从历史上看,ARCH模型最早的推广之一便是ARCH的广义形式,即GARCH(Generalized ARCH)模型。
与ARCH相比,GARCH模型的主要优势在于它更为简洁,且在拟合样本数据时无需长滞后结构。在本文中,我想描述GARCH模型,并且最重要的是,提供一个基于该模型的现成的波动率预测工具,因为预测是分析金融数据时的主要目标之一。
作者:Evgeniy Chernish