文章 "您应当知道的 MQL5 向导技术（第 11 部分）：数字墙"
请检查一下这个表格：
如果我尝试重复此操作，结果会不同：
| 第 0 行 | 0 | 0 | 0 | 0 |
| 第 1 行 | 1 | 1 | 1 | 1 |
| 第 2 行 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| 计算1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| 计算2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| 计算3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| 第 3 行 | 1 - 2x + x^2 | -1 +5x + x^2 |
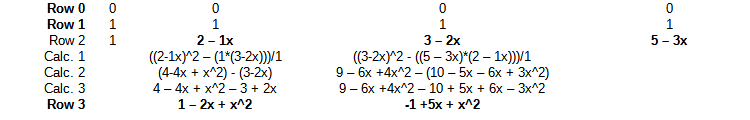
Carl Schreiber #:
请检查一下这个表格：
如果我尝试重复此操作，结果会不同：
| 第 0 行 | 0 | 0 | 0 | 0 |
| 第 1 行 | 1 | 1 | 1 | 1 |
| 第 2 行 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| 计算1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| 计算2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| 计算3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| 第 3 行 | 1 - 2x + x^2 | -1 +5x + x^2 |
您好、
刚刚看到这个问题。让我看一下，然后再回复。
Pse 见下文：
这不是证明等式的方法，但我认为代数还不错。
抱歉没有
似乎只有你的例子行得通（你真的需要这个例子吗？
| 第 0 行 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 第 1 行 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
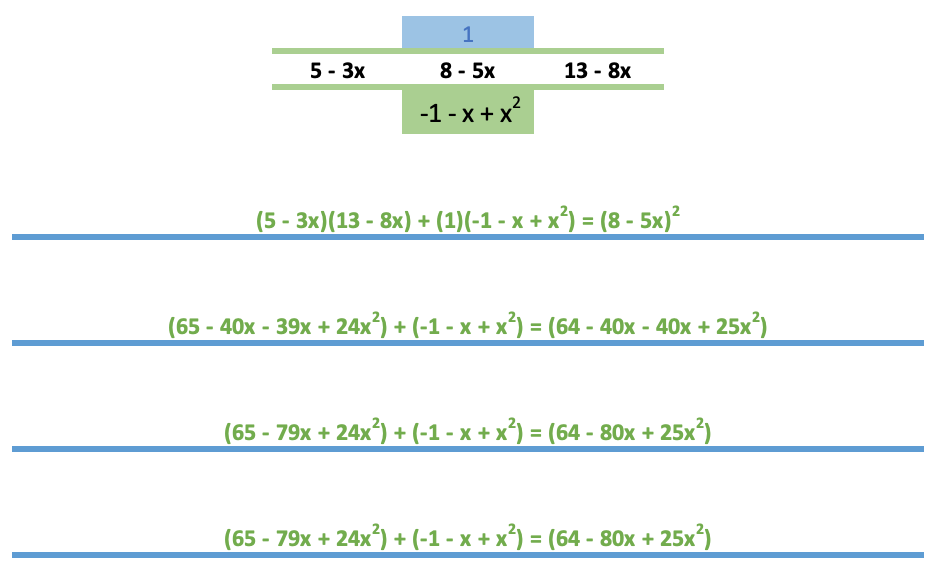
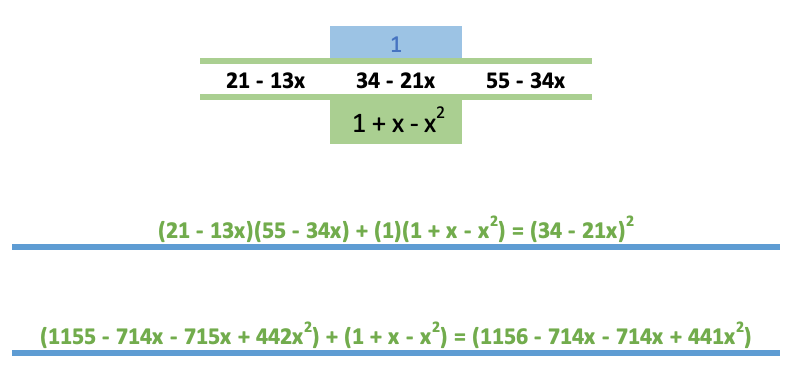
| 第 2 行 | 1 | 2 - 1x | 3 - 2x | 5 - 3x | 8 - 5x | 13 - 8x | 31 - 13x |
| 计算1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | (5 - 3x)^2 - ( (3 - 2x)(8 - 5x)) | (8 - 5x)^2 - (5 - 3x)(13 - 8x) | (13 - 8x)^2 - ( (8 - 5x)(31 - 13x) ) | ||
| 计算2 | (4 - 4x + x^2) - (3 - 2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | 25 - 30x + 9x^2 - (24 - 15x +16x + 10x^2) | 64 - 80x +25x^2 - (65 - 39x - 40x + 24x) | 169 - 208x + 64x^2 - (248 - 104x - 155x + 65x^2) | ||
| 计算3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | 25 - 30x + 9x^2 - 24 + 15x - 16x - 10x^2) | 64 - 80x +25x^2 - 65 + 39x + 40x - 24x) | 169 - 208x + 64x^2 - 248 + 104x + 155x - 65x^2) | ||
| 第 3 行 | 1 - 2x + x^2 | -1 +5x + x^2 | 1 - 31x - x^2 | -1 - 1x + x^2 | -79 - 51x - 1x^2 |
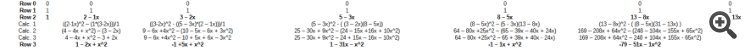
Quotient-Difference Table -- from Wolfram MathWorld
- mathworld.wolfram.com
A quotient-difference table is a triangular array of numbers constructed by drawing a sequence of n numbers in a horizontal row and placing a 1 above each. An additional "1" is then placed at the beginning and end of the row of 1s, and the value of rows underneath the original row is then determined by looking at groups of adjacent numbers N ; W X E; S (1) and computing S=(X^2-EW)/N (2) for the elements falling within a triangle formed by the diagonals extended from the...
附加的文件：
我想把它们都看一遍，但是，你懂的......
是的，除了第一种计算方法外，您都是对的--也许是您选择了不幸的计算方法。
1 - 2x + x^2 与您交替计算的结果-1 - 1x + x^2 和 1 +1x - x^2 是一致的：(
附加的文件：
https:// www.mql5.com/en/forum/461644#comment_53343777
Discussing the article: "MQL5 Wizard Techniques you should know (Part 11): Number Walls"
- 2024.01.31
- MetaQuotes
- www.mql5.com
Check out the new article: MQL5 Wizard Techniques you should know (Part 11): Number Walls . Author: Stephen Njuki...
新文章 您应当知道的 MQL5 向导技术（第 11 部分）：数字墙已发布：
数字墙（Number Walls）是线性回移寄存器的一种变体，其通过检查收敛性来预筛选序列来达到可预测性。我们看看这些思路如何运用在 MQL5。
对于少量时间序列，可以依据序列中出现的先前值为序列中的下一个值设计一个公式。数字墙允许遵照交叉规则以矩阵的形式，初步生成“数字墙”来达成这一点。在生成这个矩阵时，主要目标是确立问题中的序列是否收敛，且数字墙交叉规则算法能愉快地回答这个问题，如果在应用几行之后，矩阵中的后续行只是零。
在这篇已发表论文中，展示了这些概念，Laurent Power 级数又名形式化 Laurent 级数（FLS），已当作框架，在使用柯西（Cauchy）乘积时以多项式格式依其算术表示这些序列。
向导组装智能系统的比较测试如下所示。它们都采用动量振荡器信号，且原则上具有类似的输入，如下所示：
它们之间的区别在于，一款智能系统使用抛物线 sar 来尾随和平仓，而另一款智能系统使用本文中讲述的数字墙算法。然而，尽管信号相同，但它们依据过去一年的 H1 时间帧、EURUSD 进行测试时，它们的报告却有所不同。
作者：Stephen Njuki