请提供实用的建议。

[删除] 2020.06.06 17:18

问题：我如何正确评估结果？

每个模块的误差都以百分比形式给出。0%是理想的结果。

________________ PARAMETERS ________________	模式1	模式2	模特3	模式4	模式5	(六) 方式6	(六) 方式7	(六) 方式8	(六) Mod 9	(六) Mod 10	(六) Mod 11	(六) Mod 12	(八)模13	(六) 14	模式15	平均误差	从尝试的情况来看
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

我希望每个模块的误差是最小的，但我也希望传播是最小的。

Alexandr Andreev 2020.06.06 17:50 #1

Сергей Таболин:

问题：我如何正确评估结果？

每个模块的误差都以百分比形式给出。0%是理想的结果。

________________ PARAMETERS ________________	模式1	模式2	模特3	模式4	模式5	(六) 方式6	(六) 方式7	(六) 方式8	(六) Mod 9	(六) Mod 10	(六) Mod 11	(六) Mod 12	(八)模13	(六) 14	模式15	平均误差	从尝试的情况来看
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

我希望每个模块的误差最小，但我也希望传播最小。

对数的乘积

ZS: 不太清楚需要什么，但对数会让错误被逐步处理，它在单一情况下（个别模块）会有更好的结果。而乘法是减少分散的一种尝试

[删除] 2020.06.06 18:05 #2

Alexandr Andreev:

对数的乘积

ZS：我不太明白到底需要什么，但对数将允许逐步处理错误，它将在单一情况下（个别模块）给出更好的结果。而乘法是为了减少传播

谢谢你。而实际情况 是怎样的呢？

Alexandr Andreev 2020.06.06 18:22 #3

Сергей Таболин:

谢谢你。而实际上，这是怎么回事呢？

可能只是产品的

选项1 )将每个单元翻译成(1-x%)的样式，然后乘以.....，答案也是减去单元的。

x%是单元格值

选项2

使用对数时，我们只需取一个单元格的值，然后从它的对数开始计算))))，越接近零值就越适合渐进式评估，即在某些基数设置下，0.1比0.01好，同样0.1比1好。对数只会有一个基数参数，这是值得玩味的。

[删除] 2020.06.06 20:51 #4

Alexandr Andreev:

也许一个简单的产品就可以了。

选项1 )将每个单元翻译成（1-x%）的样式，然后将它们相乘.....，答案也要从单元中减去。

x%是单元格值

选项2

使用对数时，我们只需取一个单元格的值，然后从它的对数开始计算))))，越接近零值就越适合渐进式评估，即在某些基数设置下，0.1比0.01好，同样0.1比1好。只会有一个对数的基础参数，值得玩味。

选项1

-3,43	-16,09	-14,82	-1,53	0,37	-16,72	-27,48	-4,70	-12,29	-4,70	-7,23	-5,33	0,37	-2,16	-5,96	10601305851,38
-4,06	-16,72	-11,66	-2,80	0,37	-18,62	-28,11	-3,43	-8,49	-4,06	-5,33	-5,33	-0,90	-0,90	-5,33	-6223799946,09
-3,43	-19,25	-15,46	-3,43	0,37	-16,72	-28,75	-5,33	-4,06	-7,23	-9,13	-4,06	0,37	-0,27	-3,43	1237520122,21

这告诉我什么呢？

选项2

-0,64640373	-1,23274206	-1,19920648	-0,40312052	0,200659451	-1,24846372	-1,45453998	-0,75587486	-1,12352498	-0,75587486	-0,91539984	-0,80140371	0,200659451	-0,49968708	-0,84260924
-0,70415052	-1,24846372	-1,10243371	-0,5797836	0,200659451	-1,292699	-1,46404221	-0,64640373	-0,97726621	-0,70415052	-0,80140371	-0,80140371	-0,2787536	-0,2787536	-0,80140371
-0,64640373	-1,30642503	-1,21642983	-0,64640373	0,200659451	-1,24846372	-1,47348697	-0,80140371	-0,70415052	-0,91539984	-1,00560945	-0,70415052	0,200659451	-0,10380372	-0,64640373

这是以0.1为底的对数

我应该用它来做什么？

我已经尝试了其他功能。只是我也要如何理解他们呢？....

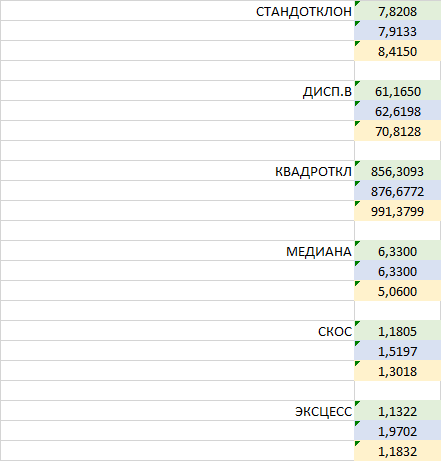
辽宁沈阳	7,8208
	7,9133
	8,4150

解释：B	61,1650
	62,6198
	70,8128

夸德拉多KL	856,3093
	876,6772
	991,3799

医学专家	6,3300
	6,3300
	5,0600

证券交易所	1,1805
	1,5197
	1,3018

超越	1,1322
	1,9702
	1,1832

Practical advice, please. Circular Buffer Issue MQL5 离题的MQL问题

Dmitry Fedoseev 2020.06.06 20:58 #5

找到每一行的最大值，然后选择具有最小最大值的那一行。请原谅我的双关语））。

[删除] 2020.06.06 21:12 #6

Dmitry Fedoseev:
找到每一行的最大值，然后选择具有最小最大值的一行。请原谅我的双关语））。

第3行中的最大值，第1行中的最小最大值。И?)))

Dmitry Fedoseev 2020.06.06 21:18 #7

Сергей Таболин:

第3行中的最大值，第1行中的最小最大值。И?)))

选择第一行。

Alexandr Andreev 2020.06.06 23:15 #8

Сергей Таболин:

选项1

-3,43	-16,09	-14,82	-1,53	0,37	-16,72	-27,48	-4,70	-12,29	-4,70	-7,23	-5,33	0,37	-2,16	-5,96	10601305851,38
-4,06	-16,72	-11,66	-2,80	0,37	-18,62	-28,11	-3,43	-8,49	-4,06	-5,33	-5,33	-0,90	-0,90	-5,33	-6223799946,09
-3,43	-19,25	-15,46	-3,43	0,37	-16,72	-28,75	-5,33	-4,06	-7,23	-9,13	-4,06	0,37	-0,27	-3,43	1237520122,21

这告诉我什么呢？

选项2

-0,64640373	-1,23274206	-1,19920648	-0,40312052	0,200659451	-1,24846372	-1,45453998	-0,75587486	-1,12352498	-0,75587486	-0,91539984	-0,80140371	0,200659451	-0,49968708	-0,84260924
-0,70415052	-1,24846372	-1,10243371	-0,5797836	0,200659451	-1,292699	-1,46404221	-0,64640373	-0,97726621	-0,70415052	-0,80140371	-0,80140371	-0,2787536	-0,2787536	-0,80140371
-0,64640373	-1,30642503	-1,21642983	-0,64640373	0,200659451	-1,24846372	-1,47348697	-0,80140371	-0,70415052	-0,91539984	-1,00560945	-0,70415052	0,200659451	-0,10380372	-0,64640373

这是以0.1为底的对数

我应该用它来做什么？

我已经尝试了其他功能。但我怎么也能理解他们呢？

这是一个婊子。"每个模块的误差都以百分比形式给出。0%是理想的结果。" 数字1意味着100%-X%或1-X*0.01

Alexandr Andreev 2020.06.06 23:19 #9

@Sergey Tabolin @Sergey Tabolin

															总数
0,9557	0,8291	0,8418	0,9747	0,9937	0,8228	0,7152	0,943	0,8671	0,943	0,9177	0,9367	0,9937	0,9684	0,9304	0,77439
0,9494	0,8228	0,8734	0,962	0,9937	0,8038	0,7089	0,9557	0,9051	0,9494	0,9367	0,9367	0,981	0,981	0,9367	0,758606
0,9557	0,7975	0,8354	0,9557	0,9937	0,8228	0,7025	0,9367	0,9494	0,9177	0,8987	0,9494	0,9937	0,9873	0,9557	0,771806

第二句是最好的，第一句和第三句非常相似

总数减去单位，即总数越接近0，结果越好.....。换句话说，到目前为止，结果不是很好，因为0.75是你的75，尽管这取决于与什么比较.....，最差的分数是1（100%），最好的分数是0。

你必须明白，90分比99分要好十倍....。99分比99.9分好十倍......事实上，只有当所有模块的错误分数都达到100分时，才有可能达到100分......。即0.1分比0.01分差十倍。同时，10分比1分差十倍。

用对数超过认为.....，答案应该是完全的正值......。通常是1.1的对数...在1到2的范围内，而不是0到1....。如果他们想增加数字，就从2开始，如果他们想逐步减少数字，就从2开始。

二次方偏差法肯定是不可能的。所有其他计算偏差的也是如此。因为理想情况下，为了了解方差，会使用线性回归的二次方差。但随后我们得到了这些偏差的估计，而没有任何数字的平均值.....

Practical advice, please.

Roman 2020.06.07 03:48 #10

Сергей Таболин:

问题：我如何正确评估结果？

每个模块的误差都以百分比形式给出。0%是理想的结果。

________________ PARAMETERS ________________	模式1	模式2	模特3	模式4	模式5	(六) 方式6	(六) 方式7	(六) 方式8	(六) Mod 9	(六) Mod 10	(六) Mod 11	(六) Mod 12	(八)模13	(六) 14	模式15	平均误差	从尝试的情况来看
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

我希望每个模块的误差最小，但我也希望散点最小。

可能更好的办法是获得模块误差的平方和，并提取根。
因此，我们将得到总模块的误差估计。
这个值越接近于零越好。
所以它是这样的。

//+------------------------------------------------------------------+
//|                                                EstimateError.mq5 |
//|                        Copyright 2020, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2020, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"


double ModN[15][3] = {{4.43, 5.06, 4.43},
                      {17.09, 17.72, 20.25},
                      {15.82, 12.66, 16.46},
                      {2.53, 3.80, 4.43},
                      {0.63, 0.63, 0.63},
                      {17.72, 19.62, 17.72},
                      {28.48, 29.11, 29.75},
                      {5.70, 4.43, 6.33},
                      {13.29, 9.49, 5.06},
                      {5.70, 5.06, 8.23},
                      {8.23, 6.33, 10.13},
                      {6.33, 6.33, 5.06},
                      {0.63, 6.33, 0.63},
                      {3.16, 1.90, 1.27},
                      {6.96, 6.33, 4.43}};

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
{
   double ModX[];
   ArrayResize(ModX, 3);
   ZeroMemory(ModX);   
   
   int    num = 1;
   double est = 0.0;
   
   for(int i=0; i<15; i++)
   {
      for(int j=0; j<3; j++)
      {
         ModX[j] = ModN[i][j];         
      }
         
      est = EstimateError(ModX);  
      
      PrintFormat("Mod"+(string)num+" EstimateError: %.3f", est); 
      num++;
   }         
}// End OnStart

//+------------------------------------------------------------------+
double EstimateError(double & arr[])
{
   int size = ArraySize(arr);
   if(size == 0 || size < 3) 
      return(0.0);
   
   //double avg       = ArrayMean(arr); 
   double max       = ArrayMax(arr);   
   double min       = ArrayMin(arr); 
   double sum_sqr_e = 0.0;
   double est_e     = 0.0;      
   
   
   for(int i=0; i<size; i++)   
      sum_sqr_e += MathPow(arr[i] - (max-min)/* или avg*/, 2.0) / (size - 2.0);
      
   est_e = MathSqrt(sum_sqr_e);   

   return(est_e);
}

//+-------------------------------------------------------------------
//Возвращает максимальное значение элементов массива
double ArrayMax(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);          
   
   double max = arrIn[0];
   for(uint i=1; i<size; i++)
      if(arrIn[i] > max) 
         max = arrIn[i];

   return(max);
}

//--------------------------------------------------------------------
//Возвращает минимальное значение элементов массива
double ArrayMin(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);   
   
   double min = arrIn[0];  
   for(uint i=1; i<size; i++)
      if(arrIn[i] < min) 
         min = arrIn[i];

   return(min);
}

//--------------------------------------------------------------------
//Возвращает средне арефметическое значение элементов массива
double ArrayMean(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);         

   double sum = 0.0;       
   for(uint i=0; i<size; i++) 
      sum += arrIn[i];     
   
   return(sum/size);
}

//--------------------------------------------------------------------

2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod1 EstimateError: 6.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod2 EstimateError: 26.422
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod3 EstimateError: 19.577
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod4 EstimateError: 3.226
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod5 EstimateError: 1.091
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod6 EstimateError: 28.540
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod7 EstimateError: 48.234
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod8 EstimateError: 6.361
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod9 EstimateError: 6.102
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod10 EstimateError: 5.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod11 EstimateError: 8.130
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod12 EstimateError: 8.098
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod13 EstimateError: 7.198
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod14 EstimateError: 1.413
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod15 EstimateError: 6.138

估计结果显示，Mod5的误差最小。

1 2 3 4 5 6 7

新评论